 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Связь потенциала и напряженности
Работа сил элект поля dA=F*dl=Eq*dl
dA=-qdφ -qdφ=Eqdl dφ=-Edl
E = - grad φ напряженность поля в данной точке равно взятому с обратным знаком градиенту потенциала в окрестности этой точки.
Напряженность поля в данной точке совпадает с направлением наиболее быстрого убывания потенциала
E=-(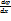 i+
i+ 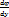 j+
j+  k)
k)
1) если поле имеет осевую симметрию, то напряженность такого поля зависит только от расстояния, от заряда до точки и не зависит от направления.E=- 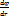
2) однородное поле E=∆φ/∆x
φ1-φ2= 
интеграл такого вида  –циркуляция вектора по контуру
–циркуляция вектора по контуру
циркуляция вектора напряженности по некоторому контуру равна разности потенциалов между нач и конеч точками этого контура.
Для замкнутого контура 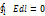
Работа в электрическом поле. Р абота по перемещению заряда из одной точки электростат поля в другую не зависит от формы траектории, а определяется только нач и конеч положением зарядов, следовательно, электростат поле явл консервативным (потенциальным) силовым полем.
Работа равна изменению потенц энергии А=-∆W=W1-W2
Поиск по сайту: