АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свободные затухающие колебания

Читайте также:
  1. V2: Свободные и вынужденные колебания
  2. Активные формы кислорода (свободные радикалы)
  3. В схеме, состоящей из конденсатора и катушки, происходят свободные электромагнитные колебания. Энергия конденсатора в произвольный момент времени t определяется выражением
  4. Вопрос 26 : Свободные гармонические механические колебания и их характеристики. Математический и физический маятники.
  5. Вопрос№15 Механические колебания. Виды колебаний. Параметры колебаний движения
  6. Вынужденные колебания. Амплитудно- частотная характеристика. Природа резонанса.
  7. Вынужденные колебания. Расчёт амплитуды и фазы
  8. Вынужденные колебания. Резонанс.
  9. Вынужденные колебания.Векторная диаграмма.Резонанс
  10. Вынужденные механические колебания.
  11. Вынужденные электромагнитные колебания. Действующие значения силы тока и напряжения.
  12. Глава II. СВОБОДНЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ НЕКОНСЕРВАТИВНОЙ СИСТЕМЕ

При затухающих колебаниях кроме квазиупругой силы в системе действует сила сопротивления среды. В рез-те происходит потеря механ энергии и амплитуда колебаний уменьшается с течением времени. При малых скоростях движения сила сопротивления среды прямо пропорциональна скорости. Fc=-rv=-rx’. r-коэф сопротивления, который зависит от формы и размеров тела и от вязкости среды. Знак «-»показывает что Fc направлена против скорости.

Дифференциальное ур-е затух колебаний ma=Fxy+Fc =>mx’’=-kx-rx’ mx’’+kx+rx’=0 x’’+ x’+ =0

x’’+2 02x=0

2 = коэф затухания 02=k/m собственная частота колебаний

Общее решение дифференциального ур-я x=A0 cos( 0) A=A0 амплитуда затух колебаний

Циклическая частота затух колебаний 2= 02- 2

Затух колебания могут происходить в системе при условии, что 0> . Вязкость среды не должна быть слишком велика.

Характеристики затух колебаний

Декремент затухания – отношение амплитуд затух колебаний, отличающиеся по времени на 1 период.

λ= = λ= =

Логарифм декремент затухания- натур логарифм отношения двух амплитуд, отличающихся по времени на 1 Т, обратно пропорциональна числу колебаний за которое амплитуда хатух колебаний уменьшается в е раз. =

энергия колеблющейся системы уменьшается с течением времени по экспоненциальному закону

E= = = =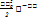E0

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)