 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Простой категорический силлогизм
Простой категорический силлогизм - это дедуктивное умозаключение, в котором из двух категорических суждений выводится новое (третье) категорическое суждение.
Посылки и заключение простого категорического силлогизма всегда содержат только три понятия, называемых терминами.
Первый термин – это субъект заключения (обозначается буквой «S»). Он также носит название меньшего термина силлогизма.
Второй термин – предикат заключения (обозначается буквой «P»). В силлогизме он считается большим термином.
Меньший и больший термины – это крайние термины силлогизма. Каждый из крайних терминов содержится не только в заключении, но и в одной из посылок. При этом: посылка, содержащая больший термин (Р), называется большей; посылка, содержащая меньший термин (S), называется меньшей. Традиционно большая посылка в силлогизме должна стоять на первом месте.
Третий термин простого категорического силлогизма называется средним (обозначается буквой «M»). Средний термин – это термин, который входит в обе посылки, но которого нет в заключении. С помощью среднего термина устанавливается связь между субъектом и предикатом заключения (между крайними терминами). Таким образом, простой категорический силлогизм - это опосредованное умозаключение, то есть умозаключение, в котором связь между двумя понятиями в заключении выявляется посредством третьего, имеющегося в обеих посылках.
Пример.
Все люди (M) смертны (P).
Сократ ( S ) – человек ( M ).
Сократ (S) смертен (P).
Данный силлогизм включает следующие термины:
«смертен» («смертны») – предикат заключения, следовательно, это больший термин (Р);
«Сократ» – субъект заключения, следовательно, это меньший термин (S);
«люди» (или в единственном числе «человек») – термин, который входит в обе посылки, но его нет в заключении, следовательно, это средний термин (М).
Суждение «Все люди (М) смертны (Р)» - большая посылка, так как содержит больший термин (Р). Суждение «Сократ (S) – человек (М)» - меньшая посылка, так как содержит меньший термин (S).
Каждый силлогизм имеет фигуру и модус.
Фигура силлогизма показывает расположение терминов (P, S, М) в посылках. В зависимости от расположения среднего термина различают четыре фигуры силлогизма (рис. 6).
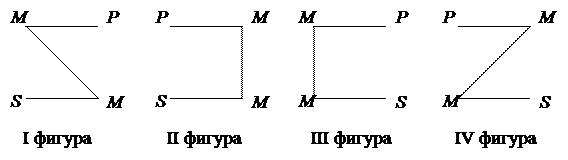
Рис. 6. Фигуры простого категорического силлогизма
Верхняя грань фигуры показывает расположение терминов в большей посылке (обратите внимание: на верхних гранях всех фигур отмечен термин Р), нижняя – расположение терминов в меньшей посылке (на нижних гранях всех фигур находится термин S).
Пример. Чтобы определить фигуру приведенного выше силлогизма (о Сократе), нужно выписать из его посылок буквенные обозначения терминов в том порядке, в котором они там расположены, соединить между собой средние термины (М) и от них провести линии к крайним (S и Р). Получим первую фигуру:

Модус простого категорического силлогизма показывает вид категорических суждений, из которых состоит силлогизм. Причем первая буква в модусе всегда показывает вид большей посылки, вторая - меньшей посылки, третья - вид заключения.
Пример. В силлогизме о Сократе обе посылки и заключение – общеутвердительные суждения, которые обозначаются буквой «А», значит, его модус – ААА.
Простые категорические силлогизмы могут быть правильными и неправильными. Правильность силлогизма зависит только от его формы (фигуры и модуса). Лишь силлогизм с правильной формой обеспечивает истинность заключения при истинности посылок.
Чтобы установить, является ли силлогизм правильным, можно проверить, соответствует ли он общим правилам силлогизмов и правилам фигур.
Общие правила силлогизмов:
1. Хотя бы одна из посылок должна быть общим суждением.
2. Хотя бы одна из посылок должна быть утвердительным суждением.
3. При частной посылке заключение должно быть частным.
4. При отрицательной посылке заключение должно быть отрицательным.
5. При двух утвердительных посылках заключение должно быть утвердительным.
6. Средний термин должен быть распределен хотя бы в одной из посылок.
7. Термин, не распределенный в посылке, не должен быть распределен в заключении.
Правила фигур:
Первая фигура: меньшая посылка должна быть утвердительной, а большая - общей.
Вторая фигура: одна из посылок должна быть отрицательной, а большая - общей.
Третья фигура: меньшая посылка должна быть утвердительной, а заключение - частным.
Для четвертой фигуры не формулируется особых правил.
Пример. Проверим, соблюдаются ли общие правила и правила фигур в следующем силлогизме:
Все юристы (Р +)
есть люди, знающие признаки преступления (М -).
Все присутствующие (S +)
есть люди, знающие признаки преступления (М -).
Все присутствующие (S +) есть юристы (Р -).
Нетрудно заметить, что здесь не соблюдается шестое из общих правил силлогизма, так как средний термин (М) оказался не распределен в обеих посылках.
Не соблюдается и правило второй фигуры (а этот силлогизм имеет вторую фигуру): обе посылки – утвердительные, тогда как правило второй фигуры требует, чтобы одна из них была отрицательной. Следовательно, данный силлогизм правильным не является.
Убедиться в правильности или неправильности силлогизма можно и другим способом – посмотрев, относится ли его модус к числу правильных модусов его фигуры.
Всего существует 256 модусов простых категорических силлогизмов (по 64 модуса в каждой фигуре). Однако не все они представляют правильные умозаключения. Правильных модусов – лишь 24 (по шесть в каждой фигуре). Среди них выделяется 19 основных, так называемых сильных модусов. Остальные – слабые модусы – могут быть представлены как сложные выводы: сочетания выводов в форме категорического силлогизма с выводами по правилам «логического квадрата» (табл. 3).
Таблица 3
Правильные модусы простого категорического силлогизма
| I фигура | II фигура | III фигура | IV фигура | |
| Сильные модусы | AAA EAE AII EIO | EAE AEE AOO EIO | AAI IAI AII EAO OAO EIO | AAI AEE IAI EAO EIO |
| Слабые модусы | AAI EAO | EAO AEO | AEO |
Пример. Приведенный выше силлогизм (о присутствующих) имеет вторую фигуру и модус ААА. Однако среди правильных модусов второй фигуры нет модуса ААА. Такой модус есть только в первой фигуре. Это также говорит о том, что силлогизм неправильный.
Поиск по сайту: