Тангенциальная составляющая ускорения 13 страница

Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения П_min, для данного вещества. Например, у инертных газов П_min мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газо­образном и твердом состояниях.

§ 61. Уравнение Ван-дер-Ваальса

Как уже указывалось в § 60, для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона — Менделеева (42.4) pV _m =RT (для моля газа), описывающее идеаль­ный газ, для реальных газов непригодны.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837—1923) вывел уравнение состояния реаль­ного газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

1. Учет собственного объема молекул. Наличие сил отталкивания, которые проти­водействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V _m, а V _m — b, где b — объем,занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в рас­чете на одну молекулу.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислени­ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр­ного объема, т. е.

(61.1)

где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного при­тяжения, V _m — молярный объем.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

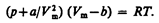(61.2)

Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV _m, уравнение Ван-дер-Ваальса примет вид

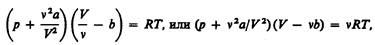
где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состоя­ний газа и решаются относительно а и b).

При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравнение состояния идеального газа.

Уравнение Ван-дер-Ваальса не единственное уравнение, описывающее реальные газы. Существу­ют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматрива­ются из-за их сложности.

§ 62. Изотермы Ван-дер-Ваальса и их анализ

Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости р от V _m при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 89) имеют довольно своеобразный характер. При высоких температурах (T > T _к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кри­вой. При некоторой температуре T _к на изотерме имеется лишь одна точка перегиба К.

Эта изотерма называется критической, соответствующая ей температура T _к — крити­ческой температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V _к, и давление р _к называются также критическими. Состояние с критическими парамет­рами (p _к, V _к, T _к) называется критическим состоянием. При низких температурах (Т < T _к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (61.2) к виду

(62.1)

Уравнение (62.1) при заданных р и Т является уравнением третьей степени от­носительно V _m; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь веществен­ные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V ₁, V ₂ и V ₃ отвечают (символ «m» для простоты опускаем) одному значению давления р ₁), второму случаю — изотермы при высоких температурах.

Рассматривая различные участки изотермы при T < Т _к (рис. 90), видим, что на участках 1 — 3 и 5 — 7 при уменьшении объема V _m давление р возрастает, что естествен­но. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообраз­ное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7 — 6—2—1. Часть 6–7 отвечает газообраз­ному состоянию, а часть 2 – 1 — жидкому. В состояниях, соответствующих горизон­тальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.

Данные выводы, следующие из анализа уравнения Ван-дер-Ваальса, были под­тверждены опытами ирландского ученого Т. Эндрюса (1813—1885), изучавшего изо­термическое сжатие углекислого газа. Отличие экспериментальных (Эндрюс) и те­оретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во вто­ром — волнообразные.

Для нахождения критических параметров подставим их значения в уравнение (62.1) в запишем

(62.2)

(символ «m» для простоты опускаем). Поскольку в критической точке все три корня совпадают и равны V _к уравнение приводится к виду

(62.3)

или

Tax как уравнения (62.2) и (62.3) тождественны, то в них должны быть равны и коэф­фициенты при неизвестных соответствующих степеней. Поэтому можно записать

(62.4)

Решая полученные уравнения, найдем

Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р,V _m под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.

Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2 — 6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть ре­ализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5— 6 и 2 — 3. Эти неустойчивые состояния называются метастабильными. Участок 2—3 изображает перегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы.

При достаточно низких температурах изотерма пересекает ось V _m, переходя в об­ласть отрицательных давлений (нижняя кривая на рис. 92). Вещество под отрицатель­ным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегре­той жидкости, участок 9—10 — растянутой жидкости.

§ 63. Внутренняя энергия реального газа

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул (определяет внутреннюю энергию идеального газа, равную С_VТ; см. § 53) и потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ (см. (61.1)):

Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, как известно из механики, идет на увеличение потенциальной энергии системы, т. е. или откуда

(постоянная интегрирования принята равной нулю). Знак минус означает, что молеку­лярные силы, создающие внутреннее давление р', являются силами притяжения (см. § 60). Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа

(63.1)

растет с повышением температуры и увеличением объема.

Если газ расширяется без теплообмена с окружающей средой (адиабатический процесс, т. е. dQ =0) и не совершает внешней работы (расширение газа в вакуум, т. е. dА= 0), то на основании первого начала термодинамики (dQ = (U ₂ —U ₁) + dA) Получим, что

(63.2)

Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется.

Равенство (63.2) формально справедливо как для идеального, так и для реального газов, но физический смысл его для обоих случаев совершенно различен. Для идеального газа равенство U ₁ =U ₂ означает равенство температур (T ₁= T ₂), т. е. при ади­абатическом расширении идеального газа в вакуум его температура не изменяется. Для реального газа из равенства (63.2), учитывая, что для моля газа

(63.3)

получаем

Так как V ₂ > V ₁, то Т ₁ > Т ₂, т. е. реальный газ при адиабатическом расширении в вакуум охлаждается. При адиабатическом сжатии в вакуум реальный газ нагревается.

§ 64. Эффект Джоуля — Томсона

Если идеальный газ адиабатически расширяется и совершает при этом работу, то он охлаждается, так как работа в данном случае совершается за счет его внутренней энергии (см. § 55). Подобный процесс, но с реальным газом — адиабатическое рас­ширение реального газа с совершением внешними силами положительной рабо­ты—осуществили английские физики Дж. Джоуль (1818—1889) и У. Томсон (лорд Кельвин, 1824—1907).

Рассмотрим эффект Джоуля — Томсона. На рис. 93 представлена схема их опыта. В теплоизолированной трубке с пористой перегородкой находятся два поршня, кото­рые могут перемешаться без трения. Пусть сначала слева от перегородки газ под поршнем 1 находится под давлением р ₁, занимает объем V ₁ при температуре Т ₁, а справа газ отсутствует (поршень 2 придвинут к перегородке). После прохождения газа через пористую перегородку в правой части газ характеризуется параметрами р ₂, V ₂, T ₂. Давления p ₁ и p ₂ поддерживаются постоянными (p ₁ >p ₂).

Так как расширение газа происходит без теплообмена с окружающей средой (адиабатически), то на основании первого начала термодинамики

(64.1)

Внешняя работа, совершаемая газом, состоит из положительной работы при движении поршня 2 (А ₂ =р ₂ V ₂) и отрицательной при движении поршня 1 (A ₁ =p ₁ V ₁), т. е. dA=A ₂ —A ₁. Подставляя выражения для работ в формулу (64.1), получаем

(64.2)

Таким образом, в опыте Джоуля — Томсона сохраняется (остается неизменной) вели­чина U+pV. Она является функцией состояния и называется энтальпией.

Ради простоты рассмотрим 1 моль газа. Подставляя в формулу (64.2) выражение (63.3) и рассчитанные из уравнения Ван-дер-Ваальса (61.2) значения p ₁ V ₂и р ₂ V ₂ (символ «m» опять опускаем) и производя элементарные преобразования, получаем

(64.3)

Из выражения (64.3) следует, что знак разности (T ₂— T ₁) зависит от того, какая из поправок Ван-дер-Ваальса играет бóльшую роль. Проанализируем данное выражение, сделав допущение, что p ₂ <<p ₁ и V ₂ >>V ₁:

1) а»0 — не учитываем силы притяжения между молекулами, а учитываем лишь размеры самих молекул. Тогда

т. е. газ в данном случае нагревается;

2) b»0 — не учитываем размеров молекул, а учитываем лишь силы притяжения между молекулами. Тогда

т. е. газ в данном случае охлаждается;

3) учитываем обе поправки. Подставив в выражение (64.3) вычисленное из уравне­ния Ван-дер-Ваальса (61.2) значение р ₁, имеем

(64.4)

т. е. знак разности температур зависит от значений начального объема V ₁ и начальной температуры Т ₁.

Изменение температуры реального газа в результате его адиабатического расшире­ния, или, как говорят, адиабатического дросселирования — медленного прохождения газа под действием перепада давления сквозь дроссель (например, пористую перегород­ку), называется эффектом Джоуля—Томсона. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (D T <0), и отрицательным, если газ нагревается (D T > 0).

В зависимости от условий дросселирования для одного и того же газа эффект Джоуля — Томсона может быть как положительным, так и отрицательным. Тем­пература, при которой (для данного давления) происходит изменение знака эффекта Джоуля — Томсона, называется температурой инверсии. Ее зависимость от объема получим, приравняв выражение (64.4) нулю:

(64.5)

Кривая, определяемая уравнением (64.5), — кривая инверсии — приведена на рис. 94. Область выше этой кривой соответствует отрицательному эффекту Джоуля — Томсона, ниже — положительному. Отметим, что при больших перепадах давления на дросселе температура газа изменяется значительно. Так, при дросселировании от 20 да 0,1 МПа и начальной температуре 17° С воздух охлаждается на 35° С.

Эффект Джоуля — Томсона обусловлен отклонением газа от идеальности. В самом деле, для моля идеального газа рV _m =RТ, поэтому выражение (64.2) примет вид

откуда следует, что Т ₁ = T ₂.

§ 65. Сжижение газов

Превращение любого газа в жидкость — сжижение газа — возможно лишь при тем­пературе ниже критической (см. § 62). При ранних попытках сжижения газов оказалось, что некоторые газы (Cl, СО₂, NH₃) легко сжижались изотермическим сжатием, а целый ряд газов (O₂, N₂, H₂, He) сжижению не поддавался. Подобные неудачные попытки объяснил Д. И. Менделеев, показавший, что сжижение этих газов производилось при температуре, большей критической, и поэтому заранее было обречено на неудачу. Впоследствии удалось получить жидкий кислород, азот и водород (их критические температуры равны соответственно 154,4, 126,1 и 33 К), а в 1908 г. нидерландский физик Г. Камерлинг-Оннес (1853—1926) добился сжижения гелия, имеющего самую низкую критическую температуру (5,3 К).

Для сжижения газов чаще применяются два промышленных метода, в основе которых используется либо эффект Джоуля—Томсона, либо охлаждение газа при совершении им работы.

Схема одной из установок, в которой используется эффект Джоуля—Томсо­на, — машины Линде * — представлена на рис. 95. Воздух в компрессоре (К) сжима­ется до давления в десятки мегапаскаль и охлаждается в холодильнике (X) до тем­пературы ниже температуры инверсии, в результате чего при дальнейшем расширении газа наблюдается положительный эффект Джоуля — Томсона (охлаждение газа при его расширении). Затем сжатый воздух проходит по внутренней трубе теплообменника (ТО) и пропускается через дроссель (Др), при этом он сильно расширяется и охлаждает­ся. Расширившийся воздух вновь засасывается по внешней трубе теплообменника, охлаждая вторую порцию сжатого воздуха, текущего по внутренней трубе. Так как каждая следующая порция воздуха предварительно охлаждается, а затем пропускается через дроссель, то температура понижается все больше. В результате 6—8-часового цикла часть воздуха (»5%), охлаждаясь до температуры ниже критической, сжижается и поступает в дьюаровский сосуд (ДС) (см. § 49), а остальная его часть возвращается в теплообменник.

* К. Линде (1842—1934) — немецкий физик и инженер.

Второй метод сжижения газов основан на охлаждении газа при совершении им работы. Сжатый газ, поступая в поршневую машину (детадер), расширяется и совер­шает при этом работу по передвижению поршня. Taк как работа совершается за счет внутренней энергии газа, то его температура при этом понижается.

Академик П. Л. Капица предложил вместо детандера применять турбодетандер, в котором газ, сжатый всего лишь до 500—600 кПа, охлаждается, совершая работу по вращению турбины. Этот метод успешно применен Капицей для сжижения гелия, предварительное охлаждение которого производилось жидким азотом. Современные мощные холодильные установки работают по принципу турбодетандера.

§ 66. Свойства жидкостей. Поверхностное натяжение

Жидкость является агрегатным состоянием вещества, промежуточным между газооб­разным и твердым, поэтому она обладает свойствами какгазообразных, так и твердых веществ. Жидкости, подобно твердым телам, обладают определенным объемом, а по­добно газам, принимают форму сосуда, в котором они находятся (см. § 28). Молекулы газа практически не связаны между собой силами межмолекулярного взаимодействия, и в данном случае средняя энергия теплового движения молекул газа гораздо больше средней потенциальной энергии, обусловленной силами притяжения между ними (см. § 60), поэтому молекулы газа разлетаются в разные стороны и газ занимает предоставленный ему объем. В твердых и жидких телах силы притяжения между молекулами уже существенны и удерживают молекулы на определенном расстоянии друг от друга. В этом случае средняя энергия хаотического (теплового) движения молекул меньше средней потенциальной энергии, обусловленной силами межмолекулярного взаимодей­ствия, и ее недостаточно для преодоления сил притяжения между молекулами, поэтому твердые тела и жидкости имеют определенный объем.

Рентгеноструктурный анализ жидкостей показал, что характер расположения ча­стиц жидкости промежуточен между газом и твердым телом. В газах молекулы движутся хаотично, поэтому нет никакой закономерности в их взаимном расположе­нии. Для твердых тел наблюдается так называемый дальний порядок в расположении частиц, т. е. их упорядоченное расположение, повторяющееся на больших расстояниях. В жидкостях имеет место так называемый ближний порядок в расположении частиц, т. е. их упорядоченное расположение, повторяющееся на расстояниях, сравнимых с межатомными.

Теория жидкости до настоящего времени полностью не развита. Разработка ряда проблем в исследовании сложных свойств жидкости принадлежит Я. И. Френкелю (1894—1952). Тепловое движение в жидкости он объяснял тем, что каждая молекула в течение некоторого времени колеблется около определенного положения равновесия, после чего скачком переходит в новое положение, отстоящее от исходного на расстоя­нии порядка межатомного. Таким образом, молекулы жидкости довольно медленно перемещаются по всей массе жидкости и диффузия происходит гораздо медленнее, чем в газах. С повышением температуры жидкости частота колебательного движения резко увеличивается, возрастает подвижность молекул, что, в свою очередь, является причи­ной уменьшения вязкости жидкости.

На каждую молекулу жидкости со стороны окружающих молекул действуют силы притяжения, быстро убывающие с расстоянием (см. рис. 88); следовательно, начиная с некоторого минимального расстояния силами притяжения между молекулами можно пренебречь. Это расстояние (порядка 10^–9 м) называется радиусом молекулярного действия r, а сфера радиуса r — сферой молекулярного действия.

Выделим внутри жидкости какую-либо молекулу А (рис. 96) и проведем вокруг нее сферу радиуса r. Достаточно, согласно определению, учесть действие на данную молекулу только тех молекул, которые находятся внутри сферы молекулярного дейст­вия. Силы, с которыми эти молекулы действуют на молекулу А, направлены в разные стороны и в среднем скомпенсированы, поэтому результирующая сила, действующая на молекулу внутри жидкости со стороны других молекул, равна нулю. Иначе обстоит дело, если молекула, например молекула В, расположена от поверхности на расстоя­нии, меньшем r. В данном случае сфера молекулярного действия лишь частично расположена внутри жидкости. Так как концентрация молекул в расположенном над жидкостью газе мала по сравнению с их концентрацией в жидкости, то равнодейст­вующая сил F, приложенных к каждой молекуле поверхностного слоя, не равна нулю и направлена внутрь жидкости. Таким образом, результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое молекулярным (или внутренним). Молекулярное давление не действует на тело, помещенное в жид­кость, так как оно обусловлено силами, действующими только между молекулами самой жидкости.

Суммарная энергия частиц жидкости складывается из энергии их хаотического (теплового) движения и потенциальной энергии, обусловленной силами межмолекуляр­ного взаимодействия. Для перемещения молекулы из глубины жидкости в поверхност­ный слой надо затратить работу. Эта работа совершается за счет кинетической энергии молекул и идет на увеличение их потенциальной энергии. Поэтому молекулы поверх­ностного слоя жидкости обладают большей потенциальной энергией, чем молекулы внутри жидкости. Эта дополнительная энергия, которой обладают молекулы в поверх­ностном слое жидкости, называемая поверхностной энергией, пропорциональна площа­ди слоя D S:

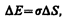(66.1)

где s — поверхностное натяжение.

Так как равновесное состояние характеризуется минимумом потенциальной энер­гии, то жидкость при отсутствии внешних сил будет принимать такую форму, чтобы при заданном объеме она имела минимальную поверхность, т. е. форму шара. Наблю­дая мельчайшие капельки, взвешенные в воздухе, можем видеть, что они действительно имеют форму шариков, но несколько искаженную из-за действия сил земного тяготе­ния. В условиях невесомости капля любой жидкости (независимо от ее размеров) имеет сферическую форму, что доказано экспериментально на космических кораблях.

Итак, условием устойчивого равновесия жидкости является минимум поверхност­ной энергии. Это означает, что жидкость при заданном объеме должна иметь наимень­шую площадь поверхности, т. е. жидкость стремится сократить площадь свободной поверхности. В этом случае поверхностный слой жидкости можно уподобить растяну­той упругой пленке, в которой действуют силы натяжения.

Рассмотрим поверхность жидкости (рис. 97), ограниченную замкнутым контуром. Под действием сил поверхностного натяжения (направлены по касательной к поверх­ности жидкости и перпендикулярно участку контура, на который они действуют) поверхность жидкости сократилась и рассматриваемый контур переместился в положе­ние, отмеченное светло-серым цветом. Силы, действующие со стороны выделенного участка на граничащие с ним участки, совершают работу

где f — сила поверхностного натяжения, действующая на единицу длины контура поверхности жидкости.

Из рис. 97 видно, что D lDx = D S, т. е.

(66.2)

Эта работа совершается за счет уменьшения поверхностной энергии, т. е.

(66.3)

Из сравнения выражений (66.1) — (66.3) видно, что

(66.4)

т. е. поверхностное натяжение s равно силе поверхностного натяжения, приходящейся на единицу длины контура, ограничивающего поверхность. Единица поверхностного натяжения — ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м²) (см. (66.4) и (бб.1)). Большинство жидкостей при температуре 300 К имеет поверхностное натяжение порядка 10^–2—10^–1 Н/м. Поверхностное натяжение с повышением тем­пературы уменьшается, так как увеличиваются средние расстояния между молекулами жидкости.

Поверхностное натяжение существенным образом зависит от примесей, имеющихся в жидкостях. Вещества, ослабляющие поверхностное натяжение жидкости, называются пoвеpxностно-активными. Наиболее известным поверхностно-активным веществом по отношению х воде является мыло. Оно сильно уменьшает ее поверхностное натяжение (примерно с 7,5 •10^–2 до 4,5 • 10^–2 Н/м). Поверхностно-активными веществами, пони­жающими поверхностное натяжение воды, являются также спирты, эфиры, нефть и др.

Поиск по сайту: