Тангенциальная составляющая ускорения 31 страница

Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведен­ный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:

(165.1)

где n ₂₁ — относительный показатель преломления второй среды относительно первой. Индексы в обозначениях углов i ₁, i '₁, i ₂ указывают, в какой среде (первой или второй) идет луч.

Относительный показатель преломления двух сред равен отношению их абсолют­ных показателей преломления:

(165.2)

Абсолютным показателем преломления среды называется величина n, равная от­ношению скорости c электромагнитных волн в вакууме к их фазовой скорости v в среде:

(165.3)

Сравнение с формулой (162.3) дает, что , где e и m — соответственно электри­ческая и магнитная проницаемости среды. Учитывая (165.2), закон преломления (165.1) можно записать в виде

(165.4)

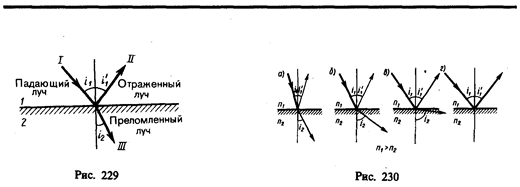
Из симметрии выражения (165.4) вытекает обратимость световых лучей. Если обратить луч III (рис.229), заставив его падать на границу раздела под углом i ₂, то преломлен­ный луч в первой среде будет распространяться под углом i ₁, т. е. пойдет в обратном направлении вдоль луча I.

Если свет распространяется из среды с большим показателем преломления n ₁ (оп­тически более плотной) в среду с меньшим показателем преломления n ₂ (оптически менее плотную) (n ₁> n ₂), например из стекла в воду, то, согласно (165.4),

Отсюда следует, что преломленный луч удаляется от нормали и угол преломления i ₂ больше,чем угол падения i ₁ (рис. 230, а).С увеличением угла падения увеличивается угол преломления (рис. 230, б, в) до тех пор, пока при некотором угле падения (i ₁= i _пр) угол преломления не окажется равным p /2. Угол i _пр называется предельным углом. При углах падения i ₁> i _пр весь падающий свет полностью отражается (рис. 230, г).

По мере приближения угла падения к предельному интенсивность преломленного луча уменьшается, а отраженного — растет (рис. 230, а—в). Если i ₁= i _пр, то интенсив­ность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 230, г). Таким образом, при углах падения в пределах от i _пр до p /2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

Предельный угол i _пр определим из формулы (165.4) при подстановке в нее i ₂= p /2.

Тогда

(165.5)

Уравнение (165.5) удовлетворяет значениям угла i _пр при n ₂£ n ₁. Следовательно, явление полного отражения имеет место только при падении света из среды оптически более плотной в среду оптически менее плотную.

Явление полного отражения используется в призмах полного отражения Показатель прелом­ления стекла равен n» 1,5, поэтому предельный угол для границы стекло — воздух равен i _пр=arcsin(1/1,5)=42°. Поэтому при падении света на границу стекло—воздух при i > 42° всегда будет иметь место полное отражение. На рис. 231, а—в показаны призмы полного отражения, позволяющие: а) повернуть луч на 90°; б) повернуть изображение; в) обернуть лучи. Такие призмы применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломле­ния, измеряя i _пр, находим относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления другой среды известен).

Явление полного отражения используется также в световодах (светопроводах), представля­ющих собой тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала. В волоконных деталях применяют стеклянное волокно, световедущая жила (сердцеви­на) которого окружается стеклом — оболочкой из другого стекла с меньшим показателем прело­мления. Свет, падающий на торец световода под углами, большими предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение н распространяется только по световедущей жиле.

Таким образом, с помощью световодов можно как угодно искривлять путь светового пучка. Диаметр световедущих жил лежит в пределах от нескольких микрометров до нескольких мил­лиметров. Для передачи изображений, как правило, применяются многожильные световоды. Вопросы передачи световых волн и изображений изучаются в специальном разделе опти­ки — волоконной оптике, возникшей в 50-е годы XX столетия. Световоды используются в элект­ронно-лучевых трубках, в электронно-счетных машинах, для кодирования информации, в медици­не (например, диагностика желудка), для целей интегральной оптики и т. д.

§ 166. Тонкие линзы. Изображение предметов с помощью линз

Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых рас­пространяется поток световой энергии. Геометрическая оптика, оставаясь приближен­ным методом построения изображений в оптических системах, позволяет разобрать основные явления, связанные с прохождением через них света, и является поэтому основой теории оптических приборов.

Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая — сферическая или плоская), преломляющими световые лучи, способные формировать оптические изоб­ражения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмас­сы и т. п. По внешней форме (рис. 232) линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые. По оптическим свойствам линзы делятся на собирающие и рассеивающие.

Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограни­чивающих линзу. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Оптический центр О линзы для простоты будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линз с оди­наковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр О лежит на пересечении главной оптической оси со сферической поверхностью).

Для вывода формулы тонкой линзы — соотношения, связывающего радиусы кри­визны R ₁ и R ₂ поверхностей линзы с расстояниями а и b от линзы до предмета и его изображения, — воспользуемся принципом Ферма,* или принципом наименьшего вре­мени: действительный путь распространения света (траектория светового луча) есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим мыслимым путем между теми же точками.

* П. Ферма (1601—1665) — французский математик и физик.

Рассмотрим два световых луча (рис. 233) — луч, соединяющий точки А и В (луч АОВ), и луч, проходящий через край линзы (луч АСВ), — воспользовавшись условием равенства времени прохождения света вдоль АОВ и АСВ. Время прохождения света вдоль АОВ

где N = n / n ₁ — относительный показатель преломления (п и n ₁ — соответственно аб­солютные показатели преломления линзы и окружающей среды). Время прохождения света вдоль АСВ равно

Так как t ₁= t ₂, то

(166.1)

Рассмотрим параксиальные (приосевые) лучи, т. е. лучи, образующие с оптической осью малые углы. Только при использовании параксиальных лучей получается стиг­матическое изображение, т. е. все лучи параксиального пучка, исходящего из точки А, пересекают оптическую ось в одной и той же точке В. Тогда h <<(a+e), h <<(b+d) и

Аналогично,

Подставив найденные выражения в (166.1), получим

(166.2)

Для тонкой линзы е << а и d << b, поэтому (166.2) можно представить в виде

Учитывая, что и соответственно d=h ² / (2 R ₁), получим

(166.3)

Выражение (166.3) представляет собой формулу тонкой линзы. Радиус кривизны выпук­лой поверхности линзы считается положительным, вогнутой — отрицательным.

Если а =¥, т. е. лучи падают на линзу параллельным пучком (рис. 234, а), то

Соответствующее этому случаю расстояние b=OF=f называется фокусным расстоянием линзы, определяемым по формуле

Оно зависит от относительного показателя преломления и радиусов кривизны.

Если b =¥, т. е. изображение находится в бесконечности и, следовательно, лучи выходят из линзы параллельным пучком (рис. 234, б), то a=OF=f. Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называют­ся фокусами линзы. Фокус — это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.

Величина

(166.4)

называется оптической силой линзы. Ее единица — диоптрия (дптр). Диоптрия — оп­тическая сила линзы с фокусным расстоянием 1 м: 1 дптр = 1/м.

Линзы с положительной оптической силой являются собирающими, с отрицатель­ной — рассевающими. Плоскости, проходящие через фокусы линзы перпендикулярно ее главной оптической оси, называются фокальными плоскостями. В отличие от собира­ющей рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси (рис. 235).

Учитывая (166.4), формулу линзы (166.3) можно записать в виде

Для рассеивающей линзы расстояния f и b надо считать отрицательными.

Построение изображения предмета в линзах осуществляется с помощью следу­ющих лучей:

1) луча, проходящего через оптический центр линзы и не изменяющего своего направления;

2) луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы;

3) луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси.

Для примера приведены построения изображений в собирающей (рис. 236) и в рас­сеивающей (рис. 237) линзах: действительное (рис. 236, а) и мнимое (рис. 236, б)изображения — в собирающей линзе, мнимое — в рассеивающей.

Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным — мнимое изобра­жение (оно прямое). Комбинации собирающих и рассеивающих линз применяются в оптических приборах, используемых для решения различных научных и технических задач.

§ 187. Аберрации (погрешности) оптических систем

Рассматривая прохождение света через тонкие линзы, мы ограничивались паракси­альными лучами (см. § 166). Показатель преломления материала линзы считали не зависящим от длины волны падающего света, а падающий свет — монохромати­ческим. Так как в реальных оптических системах эти условия не выполняются, то в них возникают искажения изображения, называемые аберрация» (или погреш­ностями).

1. Сферическая аберрация. Если расходящийся пучок света падает на линзу, то параксиальные лучи после преломления пересекаются в точке S' (на расстоянии OS' от оптического центра линзы), а лучи, более удаленные от оптической оси, — в точке S", ближе к линзе (рис. 238). В результате изображение светящейся точки на экране, перпендикулярном оптической оси, будет в виде расплывчатого пятна. Этот вид погрешности, связанный со сферичностью преломляющих поверхностей, называется сферической аберрацией. Количественной мерой сферической аберрации является от­резок d = OS'' – OS'. Применяя диафрагмы (ограничиваясь параксиальными лучами), можно сферическую аберрацию уменьшить, однако при этом уменьшается светосила линзы. Сферическую аберрацию можно практически устранить, составляя системы из собирающих (d <0) и рассеивающих (d >0) линз. Сферическая аберрация является частным случаем астигматизма.

2. Кома. Если через оптическую систему проходит широкий пучок от светящейся точки, расположенной не на оптической оси, то получаемое изображение этой точки будет в виде освещенного пятнышка, напоминающего кометный хвост. Такая погреш­ность называется поэтому комой. Устранение комы производится теми же приемами, что и сферической аберрации.

3. Дисторсия. Погрешность, при которой при больших углах падения лучей на линзу линейное увеличение для точек предмета, находящихся на разных расстояниях от главной оптической оси, несколько различается, называется дисторсией. В результате нарушается геометрическое подобие между предметом (прямоугольная сетка, рис. 239, а) и его изображением (рис. 239, б — подушкообразная дисторсия, рис. 239, в — бочкообразная дисторсия). Дисторсия особенно опасна в тех случаях, когда оптические системы применяются для съемок, например при аэрофотосъемке, в микро­скопии и т.д. Дисторсию исправляют соответствующим подбором составляющих частей оптической системы.

4. Хроматическая аберрация. До сих пор мы предполагали, что коэффициенты преломления оптической системы постоянны. Однако это утверждение справедливо лишь для освещения оптической системы монохроматическим светом (l = const); при сложном составе света необходимо учитывать зависимость коэффициента преломления вещества линзы (и окружающей среды, если это не воздух) от длины волны (явление дисперсии). При падении на оптическую систему белого света отдельные составляющие его монохроматические лучи фокусируются в разных точках (наибольшее фокусное расстояние имеют красные лучи, наименьшее — фиолетовые), поэтому изображение размыто и по краям окрашено. Это явление называется хроматической аберрацией. Так как разные сорта стекол обладают различной дисперсией, то, комбинируя собира­ющие и рассеивающие линзы из различных стекол, можно совместить фокусы двух (ахроматы) и трех (апохроматы) различных цветов, устранив тем самым хроматичес­кую аберрацию. Системы, исправленные на сферическую и хроматическую аберрации, называются апланатами.

5. Астигматизм. Погрешность, обусловленная неодинаковостью кривизны оптичес­кой поверхности в разных плоскостях сечения падающего на нее светового пучка, называется астигматизмом. Так, изображение точки, удаленной от главной оптической оси, наблюдается на экране в виде расплывчатого пятна эллиптической формы. Это пятно в зависимости от расстояния экрана до оптического центра линзы вырождается либо в вертикальную, либо в горизонтальную прямую. Астигматизм исправляется подбором радиусов кривизны преломляющих поверхностей и их фокусных расстояний. Системы, исправленные на сферическую и хроматическую аберрации и астигматизм, называются анастигматами.

Устранение аберраций возможно лишь подбором специально рассчитанных слож­ных оптических систем. Одновременное исправление всех погрешностей—задача крайне сложная, а иногда даже неразрешимая. Поэтому обычно устраняются полно­стью лишь те погрешности, которые в том или ином случае особенно вредны.

§ 168. Основные фотометрические величины и их единицы

Фотометрия — раздел оптики, занимающийся вопросами измерения интенсивности света и его источников. В фотометрии используются следующие величины:

1) энергетические — характеризуют энергетические параметры оптического излуче­ния безотносительно к его действию на приемники излучения;

2) световые — характеризуют физиологические действия света и оцениваются по воздействию на глаз (исходят из так называемой средней чувствительности глаза) или другие приемники излучения.

1. Энергетические величины. Поток излучения Ф _е — величина, равная отношению энергии W излучения ко времени t, за которое излучение произошло:

Единица потока излучения — ватт (Вт).

Энергетическая светимость (излучательность) R_e — величина, равная отношению потока излучения Ф _e, испускаемого поверхностью, к площади S сечения, сквозь которое этот поток проходит:

т. е. представляет собой поверхностную плотность потока излучения.

Единица энергетической светимости — ватт на метр в квадрате (Вт/м²).

Энергетическая сила света (сила излучения) I_e определяется с помощью понятия о точечном источнике света — источнике, размерами которого по сравнению с рассто­янием до места наблюдения можно пренебречь. Энергетическая сила света I_e — величина, равная отношению потока излучения Ф _e источника к телесному углу w, в пределах которого это излучение распространяется:

Единица энергетической силы света — ватт на стерадиан (Вт/ср).

Энергетическая яркость (лучистость) B_e — величина, равная отношению энергети­ческой силы света D I_e, элемента излучающей поверхности к площади D S проекции этого элемента на плоскость, перпендикулярную направлению наблюдения:

Единица энергетической яркости — ватт на стерадиан-метр в квадрате (Вт/(ср × м²)).

Энергетическая освещенность (облученность) Е_е характеризует величину потока из­лучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности совпадает с единицей энергетической светимости (Вт/м²).

2. Световые величины. При оптических измерениях используются различные при­емники излучения (например, глаз, фотоэлементы, фотоумножители), которые не об­ладают одинаковой чувствительностью к энергии различных длин волн, являясь, таким образом, селективными (избирательными). Каждый приемник излучения характеризует­ся своей кривой чувствительности к свету различных длин волн. Поэтому световые измерения, являясь субъективными, отличаются от объективных, энергетических и для них вводятся световые единицы, используемые только для видимого света. Основной световой единицей в СИ является единица силы света — кандела (кд), определение которой дано выше (см. Введение). Определение световых единиц аналогично энергетическим.

Световой поток Ф определяется как мощность оптического излучения по вызыва­емому им световому ощущению (по его действию на селективный приемник света с заданной спектральной чувствительностью).

Единица светового потока — люмен (лм): 1 лм — световой поток, испускаемый точечным источником силой света в 1 кд внутри телесного угла в 1 ср (при равномер­ности поля излучения внутри телесного угла) (1 лм = 1 кд × ср).

Светимость R определяется соотношением

Единица светимости — люмен на метр в квадрате (лм/м²).

Яркость В_j светящейся поверхности в некотором направлении j есть величина, равная отношению силы света I в этом направлении к площади S проекции светящейся поверхности на плоскость, перпендикулярную данному направлению:

Единица яркости — кандела на метр в квадрате (кд/м²).

Освещенность Е — величина, равная отношению светового потока Ф, падающего на поверхность, к площади S этой поверхности:

Единила освещенности — люкс (лк): 1 лк — освещенность поверхности, на 1 м² которой падает световой поток в 1 лм (1 лк= 1 лм/м²).

§ 189. Элементы электронной оптики

Область физики и техники, в которой изучаются вопросы формирования, фокусировки и отклонения пучков заряженных частиц и получения с их помощью изображений под действием электрических и магнитных полей в вакууме, называется электронной оптикой. Комбинируя различные электронно-оптические элементы — электронные линзы, зеркала, призмы, — создают электронно-оптические приборы, например электрон­но-лучевую трубку, электронный микроскоп, электронно-оптический преобразователь.

1. Электронные линзы представляют собой устройства, с помощью электрических и магнитных полей которых формируются и фокусируются пучки заряженных частиц. Существуют электростатические и магнитные линзы. В качестве электростатической линзы может быть использовано электрическое поле с вогнутыми и выпуклыми эквипотенциальными поверхностями, например в системах металлических электродов и диафрагм, обладающих осевой симметрией. На рис. 240 изображена простейшая собирающая электростатическая линза, где А — точка предмета, В — ее изображение, пунктиром изображены линии напряженности поля.

Магнитная линза обычно представляет собой соленоид с сильным магнитным полем, коаксиальным пучку электронов. Чтобы магнитное поле сконцентрировать на оси симметрии, соленоид помещают в железный кожух с узким внутренним кольцевым разрезом.

Если расходящийся пучок заряженных частиц попадает в однородное магнитное поле, направ­ленное вдоль оси пучка, то скорость каждой частицы можно разложить на два компонента: поперечный и продольный. Первый из них определит равномерное движение по окружности в плоскости, перпендикулярной направлению поля (см. § 115), второй — равномерное прямолинейное движение вдоль поля. Результирующее движение частицы будет происходить по спирали, ось которой совпадает с направлением поля. Для электронов, испускаемых под различными углами, нормальные составляющие скоростей будут различны, т. е. будут различны и радиусы описываемых ими спиралей. Однако отношение нормальных составляющих скорости к радиусам спиралей за период вращения (см. § 115) будет для всех электронов одинаково; следовательно, через один оборот все электроны сфокусируются в одной и той же точке на оси магнитной линзы.

«Преломление» электростатических и магнитных линз зависит от их фокусных расстояний, которые определяются устройством линзы, скоростью электронов, раз­ностью потенциалов, приложенной к электродам (электростатическая линза), и индук­цией магнитного поля (магнитная линза). Изменяя разность потенциалов или регули­руя ток в катушке, можно изменить фокусное расстояние линз. Стигматическое изоб­ражение предметов в электронных линзах получается только для параксиальных электронных пучков. Как и в оптических системах (см. § 167), в электронно-оптических элементах также имеют место погрешности: сферическая аберрация, кома, дисторсия, астигматизм. При разбросе скоростей электронов в пучке наблюдается также и хрома­тическая аберрация. Аберрации ухудшают разрешающую способность и качество изображения, а поэтому в каждом конкретном случае необходимо их устранять.

2. Электронный микроскоп — устройство, предназначенное для получения изображения микрообъектов; в нем в отличие от оптического микроскопа вместо световых лучей используют ускоренные до больших энергий (30—100 кэВ и более) в условиях глубокого вакуума (примерно 0,1 мПа) электронные пучки, а вместо обычных линз — электронные линзы. В электронных микроскопах предметы рассматриваются либо в проходящем, либо в отраженном потоке электронов, поэтому различают просвечивающие и отражательные электронные микроскопы.

На рис. 241 приведена принципиальная схема просвечивающего электронного микроскопа. Электронный пучок, формируемый электронной пушкой 1, попадает в область действия конденсорной линзы 2, которая фокусирует на объекте 3 элект­ронный пучок необходимого сечения и интенсивности. Пройдя объект и испытав в нем отклонения, электроны проходят вторую магнитную линзу — объектив 4 — и собира­ются ею в промежуточное изображение 5. Затем с помощью проекционной линзы 6 на флуоресцирующем экране достигается окончательное изображение 7.

Разрешающая способность электронного микроскопа ограничивается, с одной сто­роны, волновыми свойствами (дифракцией) электронов, с другой — аберрациями элек­тронных линз. Согласно теории, разрешающая способность микроскопа пропорци­ональна длине волны, а так как длина волны применяемых электронных пучков (примерно 1 пм) в тысячи раз меньше длины волны световых лучей, то разрешение электронных микроскопов соответственно больше и составляет 0,01 — 0,0001 мкм (для оптических микроскопов приблизительно равно 0,2 — 0,3 мкм). С помощью электронных микроскопов можно добиться значительно больших увеличений (до 10⁶ раз), что позволяет наблюдать детали структур размерами 0,1 нм.

Поиск по сайту: