Тангенциальная составляющая ускорения 42 страница

т. е. для дискретного набора отрицательных значений энергии.

Таким образом,как и в случае «потенциальной ямы» с бесконечно высокими «стенками» (см. § 220) и гармонического осциллятора (см. § 222), решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е ₁, E ₂, Е ₃ ,... показаны на рис. 302 в виде горизонтальных прямых. Самый нижний уровень Е ₁, отвечающий минимальной возможной энер­гии, — основной, все остальные (Е_n >Е ₁, n = 2, 3,...) — возбужденные (см. § 212). При Е <0 движение электрона является связанным — он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n =¥ E _¥ = 0. При Е >0 движение электрона является свободным; область непрерывного спектра Е >0 (заштри­хована на рис. 302) соответствует ионизованному атому. Энергия ионизации атома водорода равна

Выражение (223.3) совпадает с формулой (212.3), полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следстви­ем самой теории, вытекают непосредственно из решения уравнения Шредингера.

2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции 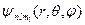, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным т_l.

Главное квантовое число n, согласно (223.3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с еди­ницы:

Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

(223.4)

где l — орбитальное квантовое число, которое при заданном n принимает значения

(223.5)

т. е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L _l момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_lx на направление z внешнего магнитного поля принимает квантованные значения, кратные ћ:

(223.6)

где т_l — магнитное квантовое число, которое при заданном l может принимать значения

(223.7)

т. е. всего 2 l +1 значений. Таким образом, магнитное квантовое число m_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2 l +1 ориентации.

Наличие квантового числа m_l должно привести в магнитном поле к расщеплению уровня с главным квантовым числом п на 2 l +1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщеп­ление энергетических уровней в магнитном поле было обнаружено в 1896 г. голландс­ким физиком П. Зееманом (1865—1945) и получило название эффекта Зеемана. Расщеп­ление уровней энергии во внешнем электрическом поле, тоже доказанное эксперимен­тально, называется эффектом Штарка*.

* И. Штарк (1874—1957) — немецкий физик.

Хотя энергия электрона (223.3) и зависит только от главного квантового числа п, но каждому собственному значению Е_n (кроме Е ₁ ) соответствует несколько собственных функций , отличающихся значениями l и m_l. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном п орбитальное квантовое число l может изменяться от 0 до п –1 (см. (223.5)), а каждому значению l соответствует 2 l +1 различных значений m_l (223.7), то число различных состояний, соответствующих данному п, равно

(223.8)

Квантовые числа и их значения являются следствием решений уравнений Шредингера и условий однозначности, непрерывности и конечности, налагаемых на волновую функцию y. Кроме того, так как при движении электрона в атоме существенны волновые свойства электрона, то квантовая механика вообще отказывается от клас­сического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в раз­личных точках объема атома. Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

В атомной физике, по аналогии со спектроскопией, состояние электрона, харак­теризующееся квантовыми числами l= 0, называют s -состоянием (электрон в этом состоянии называют s -электроном), l =1 — p -состоянием, l= 2 — d -состоянием, l =3 — f -состоянием и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях n =2 и l =0 и 1 обозначаются соответственно символами 2 s и 2 р.

На рис. 303 для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при n =1 и п= 2, определяемое | |². Как видно из рисунка, оно зависит от n, l и m_l. Так, при l =0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически-симмет­рична), а для остальных состояний в центре равна нулю и зависит от направления.

3. Спектр. Квантовые числа n, l и m_l позволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора (см. рис. 294).

В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Те­оретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа D l удовлетворяет условию

(223.9)

2) изменение магнитного квантового числа D m_l удовлетворяет условию

В оптических спектрах указанные правила отбора в основном выполняются. Одна­ко в принципе могут наблюдаться и слабые «запрещенные» линии, например воз­никающие при переходах с D l = 2. Появление этих линий объясняется тем, что строгая теория, запрещая дипольные переходы, разрешает переходы, соответствующие излуче­нию более сложных систем зарядов, например квадруполей. Вероятность же квадрупольных переходов (переходы с D l =2) во много раз меньше вероятности дипольных переходов, поэтому «запрещенные» линии и являются слабыми.

Учитывая число возможных состояний, соответствующих данному n, и правило отбора (223.9), рассмотрим спектральные линии атома водорода (рис. 304): серии Лаймана соответствуют переходы

серии Бальмера —

и т. д.

Переход электрона из основного состояния в возбужденное обусловлен увеличени­ем энергии атома и может происходить только при сообщении атому энергии извне, например за счет поглощения атомом фотона. Так как поглощающий атом находится обычно в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 1 s®np (n = 2, 3,...), что находится в полном согласии с опытом.

§ 224. 1s-Состояние электрона в атоме водорода

1 s -Состояние электрона в атоме водорода является сферически-симметричным, т. е. не зависит от углов q и j. Волновая функция y электрона в этом состоянии определяется только расстоянием r электрона от ядра, т. е. y = y ₁₀₀(r), где цифры в индексе соответ­ственно указывают, что п= 1, l= 0 и m_l =0. Уравнению Шредингера для 1 s -состояния электрона в атоме водорода удовлетворяет функция вида

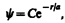(224.1)

где, как можно показать, — величина, совпадающая с первым боровским радиусом а (см. (212.2)) для атома водорода, С — некоторая постоянная, опреде­ляемая из условия нормировки вероятностей (216.3).

Благодаря сферической симметрии y -функции вероятность обнаружения электрона на расстоянии r одинакова по всем направлениям. Поэтому элемент объема d V, отвечающий одинаковой плотности вероятности, обычно представляют в виде объема сферического слоя радиусом r и толщиной d r: d V =4p r ²d r. Тогда, согласно условию нормировки вероятностей (216.3) с учетом (224.1),

После интегрирования получим

(224.2)

Подставив выражение (224.2) в формулу (224.1), определим нормированную волновую функцию, отвечающую 1 s -состоянию электрона в атоме водорода:

(224.3)

Вероятность обнаружить электрон в элементе объема (см. (216.2)) равна

Подставив в эту формулу волновую функцию (224.3), получим

Вычислим те расстояния r _max от ядра, на которых электрон может быть обнаружен с наибольшей вероятностью. Исследуя выражение d W/ d r на максимум, получим, что r _max= a. Следовательно, электрон может быть обнаружен с наибольшей вероятностью на расстояниях, равных боровскому радиусу, т. е. имеется равная и наибольшая вероятность обнаружения электрона во всех точках, расположенных на сферах радиуса а с центром в ядре атома. Казалось бы, квантово-механический расчет дает полное согласие с теорией Бора. Однако, согласно квантовой механике, плотность вероятности лишь при r=а достигает максимума, оставаясь отличной от нуля во всем пространстве (рис. 305). Таким образом, в основном состоянии атома водорода наиболее вероятным расстоянием от электрона до ядра является расстояние, равное боровскому радиусу. В этом заключается квантово-механический смысл боровского радиуса.

§ 225. Спин электрона. Спиновое квантовое число

О. Штерн и В. Герлах, проводя прямые измерения магнитных моментов (см. § 131), обнаружили в 1922 г., что узкий пучок атомов водорода, заведомо находящихся в s -состоянии, в неоднородном магнитном поле расщепляется на два пучка. В этом состоянии момент импульса электрона равен нулю (см. (223.4)). Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механичес­кому моменту (см. (131.3)), поэтому он равен нулю и магнитное поле не должно оказывать влияния на движение атомов водорода в основном состоянии, т. е. расщеп­ления быть не должно. Однако в дальнейшем при применении спектральных приборов с большой разрешающей способностью было доказано, что спектральные линии атома водорода обнаруживают тонкую структуру (являются дублетами) даже в отсутствие магнитного поля.

Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек (1900—1974) и С. Гаудсмит (1902—1979) предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, спином (см. §131).

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) L _s, то ему соответствует собственный магнитный момент р _ms. Согласно общим выво­дам квантовой механики, спин квантуется по закону

где s — спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_sz спина квантуется так, что вектор L _s может принимать 2 s +1 ориентации. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2 s +1=2, откуда s = ½. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением, аналогичным (223.6):

где т_s — магнитное спиновое квантовое число; оно может иметь только два значения: m_s = ± ½.

Таким образом, опытные данные привели к необходимости характеризовать элект­роны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.

§ 226. Принцип неразличимости тождественных частиц. Фермионы и бозоны

Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналога в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства — массу, электрический заряд, спин и другие внутренние характеристики (например, квантовые числа). Такие частицы называют тождественными.

Необычные свойства системы одинаковых тождественных частиц проявляются в фундаментальном принципе квантовой механики — принципе неразличимости тож­дественных частиц, согласно которому невозможно экспериментально различить тож­дественные частицы.

В классической механике даже одинаковые частицы можно различить по положе­нию в пространстве и импульсам. Если частицы в какой-то момент времени пронуме­ровать, то в следующие моменты времени можно проследить за траекторией любой из них. Классические частицы, таким образом, обладают индивидуальностью, поэтому классическая механика систем из одинаковых частиц принципиально не отличается от классической механики систем из различных частиц.

В квантовой механике положение иное. Из соотношения неопределенностей вытека­ет, что для микрочастиц вообще неприменимо понятие траектории; состояние микроча­стицы описывается волновой функцией, позволяющей вычислять лишь вероятность (| y |²) нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, вообще лишен смысла: можно лишь говорить о вероятности нахождения в данной области одной из тождест­венных частиц. Таким образом, в квантовой механике тождественные частицы полно­стью теряют свою индивидуальность и становятся неразличимыми. Следует подчерк­нуть, что принцип неразличимости тождественных частиц не является просто следстви­ем вероятностной интерпретации волновой функции, а вводится в квантовую механику как новый принцип, который, как уже указывалось, является фундаментальным.

Принимая во внимание физический смысл величины | y |², принцип неразличимости тождественных частиц можно записать в виде

(226.1)

где x ₁ и х ₂ — соответственно совокупность пространственных и спиновых координат первой и второй частиц. Из выражения (226.1) вытекает, что возможны два случая:

т. е. принцип неразличимости тождественных частиц ведет к определенному свойству симметрии волновой функции. Если при перемене частиц местами волновая функция не меняет знака, то она называется cимметричной, если меняет — антисимметричной. Изменение знака волновой функции не означает изменения состояния, так как физичес­кий смысл имеет лишь квадрат модуля волновой функции. В квантовой механике доказывается, что характер симметрии волновой функции не меняется со временем. Это же является доказательством того, что свойство симметрии или антисиммет­рии — признак данного типа микрочастиц.

Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются ан­тисимметричными волновыми функциями и подчиняются статистике Ферми — Дира­ка; эти частицы называются фермионами. Частицы с нулевым или целочисленным спином (например, p-мезоны, фотоны) описываются симметричными волновыми функ­циями и подчиняются статистике Бозе — Эйнштейна; эти частицы называются бозонами. Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спив — полуцелый), а из четно­го — бозонами (суммарный спин целый).

Зависимость характера симметрии волновых функций системы тождественных частиц от спина частиц теоретически обоснована швейцарским физиком В. Паули (1900—1958), что явилось еще одним доказательством того, что спин является фун­даментальной характеристикой микрочастиц.

§ 227. Принцип Паули. Распределение электронов в атоме по состояниям

Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметрич­ной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых ан­тисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).

Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения квантовой механики: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:

Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел п, l, m_l и т_s т. е.

где Z (п, l, m_l, т_s) — число электронов, находящихся в квантовом состоянии, описыва­емом набором четырех квантовых чисел: п, l, m_l, т_s. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Согласно формуле (223.8), данному n соответствует n ² различных состояний, от­личающихся значениями l и m_l. Квантовое число т_s может принимать лишь два значения (± ½). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно

Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n –1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке опреде­ляется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2 l +1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 6.

Таблица 6

§ 228. Периодическая система элементов Менделеева

Принцип Паули, лежащий в основе систематики заполнения электронных состояний в атомах, позволяет объяснить Периодическую систему элементов Д. И. Менделеева (1869) — фундаментального закона природы, являющегося основой современной химии, атомной и ядерной физики.

Д. И. Менделеев ввел понятие порядкового номера Z химического элемента, рав­ного числу протонов в ядре и соответственно общему числу электронов в электронной оболочке атома. Расположив химические элементы по мере возрастания порядковых номеров, он получил периодичность в изменении химических свойств элементов. Однако для известных в то время 64 химических элементов некоторые клетки таблицы оказались незаполненными, так как соответствующие им элементы (например, Ga, Se, Ос) тогда еще не были известны. Д. И. Менделеев, таким образом, не только правиль­но расположил известные элементы, но и предсказал существование новых, еще не открытых элементов и их основные свойства. Кроме того, Д. И. Менделееву удалось уточнить атомные веса некоторых элементов. Например, атомные веса Be и U, вычисленные на основе таблицы Менделеева, оказались правильными, а полученные ранее экспериментально — ошибочными.

Так как химические и некоторые физические свойства элементов объясняются внешними (валентными) электронами в атомах, то периодичность свойств химических элементов должна быть связана с определенной периодичностью в расположении электронов в атомах. Поэтому для объяснения таблицы будем считать, что каждый последующий элемент образован из предыдущего прибавлением к ядру одного прото­на и соответственно прибавлением одного электрона в электронной оболочке атома. Взаимодействием электронов пренебрегаем, внося, где это необходимо, соответст­вующие поправки. Рассмотрим атомы химических элементов, находящиеся в основном состоянии.

Единственный электрон атома водорода находится в состоянии 1 s, характеризу­емом квантовыми числами п= 1, l= 0, m_l =0 и m_s =± ½; (ориентация его спина произвольна). Оба электрона атома Не находятся в состоянии 1 s, но с антипараллельной ориентацией спина. Электронная конфигурация для атома Не записывается как 1 s ²(два 1 s -электрона). На атоме Не заканчивается заполнение K -оболочки, что соответствует завершению I периода Периодической системы элементов Менделеева (табл. 7).

Таблица 7

Третий электрон атома Li (Z =3), согласно принципу Паули, уже не может раз­меститься в целиком заполненной K -оболочке и занимает наинизшее энергетическое состояние с n =2 (L -оболочка), т.е. 2 s -состояние. Электронная конфигурация для атома Li: 1 s ²2 s. Атомом Li начинается II период Периодической системы элементов. Четвертым электроном Be (Z =4) заканчивается заполнение подоболочки 2 s. У следу­ющих шести элементов от В (Z= 5 ) до Ne (Z= 10) идет заполнение подоболочки 2 р (табл. 7). II период Периодической системы заканчивается неоном — инертным газом, для которого подоболочка 2 р целиком заполнена.

Одиннадцатый электрон Na (Z =11) размещается в М -оболочке (n =3), занимая наинизшее состояние 3 s. Электронная конфигурация имеет вид 1 s ²2 s ²2 p ⁶3 s. 3 s -Электрон (как и 2 s -электрон Li) является валентным электроном, поэтому оптические свойства Na подобны свойствам Li. С Z= 12 идет последовательное заполнение M -оболочки. Аr (Z =18) оказывается подобным Не и Ne: в его наружной оболочке все s- и p -состояния заполнены. Аr является химически инертным и завершает III период Периодической системы.

Девятнадцатый электрон К (Z =19) должен был бы занять 3 d -состоянис в M -оболочке. Однако и в оптическом, и в химическом отношениях атом К схож с атомами Li и Na, которые имеют внешний валентный электрон в s -состоянии. Поэтому 19-й валентный электрон К должен также находиться в s -состоянии, но это может быть только s -состояние новой оболочки (N -оболочки), т. е. заполнение N -обо­лочки для К начинается при незаполненной M -оболочке. Это означает, что в резуль­тате взаимодействия электронов состояние n =4, l =0 имеет меньшую энергию, чем состояние n =3, l= 2. Спектроскопические и химические свойства Са (Z =20) показыва­ют, что его 20-й электрон также находится в 4 s -состоянии N -оболочки. В последующих элементах происходит заполнение M -оболочки (от Sc (Z= 21) до Zn (Z =30)). Далее N -оболочка заполняется до Кr (Z =36), у которого опять-таки, как и в случае Ne и Аr,

s- и p -состояния наружной оболочки заполнены целиком. Криптоном заканчивается IV период Периодической системы. Подобные рассуждения применимы и к остальным элементам таблицы Менделеева, однако эти данные можно найти в справочниках. Отметим лишь, что и начальные элементы последующих периодов Rb, Cs, Fr являются щелочными металлами, а их последний электрон находится в s -состоянии. Кроме того, атомы инертных газов (Не, Ne, Ar, Кr, Хе, Rn) занимают в таблице особое положе­ние — в каждом из них s - и p- состояния наружной оболочки целиком заполнены и ими завершаются очередные периоды Периодической системы.

Каждую из двух групп элементов — лантаниды (от лантана (Z =57) до лютеция (Z =71)) и актиниды (от актиния (Z =89) до лоуренсия (Z =103)) — приходится поме­щать в одну клетку таблицы, таккак химические свойства элементов в пределах этих групп очень близки. Это объясняется тем, что для лантанидов заполнение подоболочки 4 f, которая может содержать 14 электронов, начинается лишь после того, как целиком заполнятся подоболочки 5 s, 5 p и 6 s. Поэтому для этих элементов внешняя P -оболочка (6 s ²) оказывается одинаковой. Аналогично, одинаковой для актинидов является Q -оболочка (7 s ²).

Поиск по сайту: