Тангенциальная составляющая ускорения 25 страница

Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и созда­ет внутри него поле, магнитную индукцию В' которого можно вычислить, учитывая формулу (119.2) для N = 1 (соленоид из одного витка):

(133.2)

где I' — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнит­ная проницаемость m принята равной единице.

С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока p = I'lS/l = I'V/l, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то намаг­ниченность магнетика

(133.3)

Сопоставляя (133.2) и (133.3), получим, что

или в векторной форме

Подставив выражения для В ₀ и В' в (133.1), получим

(133.4)

или

(133.5)

Как показывает опыт, в несильных полях намагниченность прямо пропорциональ­на напряженности поля, вызывающего намагничение, т. е.

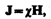(133.6)

где c — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнстихов c отрицательна (поле молекулярных токов противоположно вне­шнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).

Используя формулу (133.6), выражение (133.4) можно записать в виде

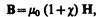(133.7)

откуда

Безразмерная величина

(133.8)

представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) В = m ₀ m Н, которое ранее постулировалось.

Так как абсолютное значение магнитной восприимчивости для диа- и парамаг­нетиков очень мало (порядка 10^–4 —10^–6), то для них m незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков c<0 и m <1, для парамагнетиков c>0 и m >1.

Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):

где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым кон­туром L. Таким образом, циркуляция вектора магнитной индукции В по произволь­ному замкнутому контуру равна алгебраической сумме токов проводимости и молеку­лярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, таким образом, характеризует результирующее поле, созданное как мак­роскопическими токами в проводниках (токами проводимости), так и микроскопичес­кими токами в магнетиках, поэтому линии вектора магнитной индукции В не имеют источников и являются замкнутыми.

Из теории известно, что циркуляция намагниченности J по произвольному замкну­тому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

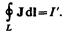
Тогда закон полного тока для магнитного поля в веществе можно записать также в виде

(133.9)

где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости.

Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор H напряженности магнитного поля. Итак, циркуляция вектора Н по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:

(133.10)

Выражение (133.10) представляет собой теорему о циркуляции вектора Н.

§ 134. Условия на границе раздела двух магнетиков

Установим связь для векторов В и Н на границе раздела двух однородных магнетиков (магнитные проницаемости m ₁ и m ₂) при отсутствии на границе тока проводимости.

Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 190). Основания D S настолько малы, что в пределах каждого из них вектор В одинаков. Согласно теореме Гаусса (120.3),

(нормали n и n' к основаниям цилиндра направлены противоположно). Поэтому

(134.1)

Заменив, согласно B = m ₀ m H, проекции вектора В проекциями вектора Н, умножен­ными на m ₀ m, получим

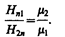(134.2)

Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDA длиной l, ориентировав его так, как показано на рис.191. Согласно теореме (133.10) о циркуляции вектора Н,

(токов проводимости на границе раздела нет), откуда

(знаки интегралов по AВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам BC и DA ничтожно малы). Поэтому

(134.3)

Заменив, согласно В = m ₀ m H, проекции вектора Н проекциями вектора В, деленными на m ₀ m, получим

(134.4)

Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора В (В_n) и тангенциальная составляющая вектора Н (Н_t) изменя­ются непрерывно (не претерпевают скачка), а тангенциальная составляющая вектора В (B_t) и нормальная составляющая вектора Н (H_n) претерпевают скачок.

Из полученных условий (134.1)—(134.4) для составляющих векторов В и Н следует, что линии этих векторов испытывают излом (преломляются). Как и в случае диэлект­риков (см. § 90), можно найти закон преломления линий В (а значит, и линий Н):

(134.5)

Из этой формулы следует, что, входя в магнетик с большей магнитной проница­емостью, линии В и Н удаляются от нормали.

§ 135. Ферромагнетики и их свойства

Помимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т. е. они намагниче­ны даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основ­ного их представителя — железа (от него и идет название «ферромагнетизм») — от­носятся, например, кобальт, никель, гадолиний, их сплавы и соединения.

Ферромагнетики помимо способности сильно намагничиваться обладают еще и другими свойствами, существенно отличающими их от диа- и парамагнетиков. Если для слабомагнитных веществ зависимость J от Н линейна (см. (133.6) и рис. 192), то для ферромагнетиков эта зависимость, впервые изученная в 1878 г. методом баллистичес­кого гальванометра для железа русским физиком А.Г. Столетовым (1839—1896), является довольно сложной. По мере возрастания Н намагниченность J сначала растет быстро, затем медленнее и, наконец, достигается так называемое магнитное насыщение J _нас, уже не зависящее от напряженности поля. Подобный характер зависимости J от Н можно объяснить тем, что по мере увеличения намагничивающего поля увеличивает­ся степень ориентации молекулярных магнитных моментов по полю, однако этот процесс начнет замедляться, когда остается все меньше и меньше неориентированных моментов, и, наконец, когда все моменты будут ориентированы по полю, дальнейшее увеличение J прекращается и наступает магнитное насыщение.

Магнитная индукция B = m ₀ (H+J) (см. (133.4)) в слабых полях растет быстро с ростом H вследствие увеличения J, а в сильных полях, поскольку второе слагаемое постоянно (J=J _нас), В растет с увеличением Н по линейному закону (рис. 193).

Существенная особенность ферромагнетиков — не только большие значения m (на­пример, для железа — 5000, для сплава супермаллоя — 800 000!), но и зависимость m от Н (рис. 194). Вначале m растет с увеличением Н, затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей к 1 (m = B /(m ₀ H) = 1 + J/H, поэтому при J = J _нас = const с ростом Н отношение J/H ® 0, m ®1).

Характерная особенность ферромагнетиков состоит также в том, что для них зависимость J от H (а следовательно, и В от Н) определяется предысторией намагниче­ния ферромагнетика. Это явление получило название магнитного гистерезиса. Если намагнитить ферромагнетик до насыщения (точка 1, рис. 195), а затем начать умень­шать напряженность Н намагничивающего поля, то, как показывает опыт, умень­шение J описывается кривой 1—2, лежащей выше кривой 1—0. При Н = 0 J отличается от нуля, т. е. в ферромагнетике наблюдается остаточное намагничение J _ос. С наличием остаточного намагничения связано существование постоянных магнитов. Намагничение обращается в нуль под действием поля Н с, имеющего направление, противоположное полю, вызвавшему намагничение. Напряженность Н с называется коэрцитивной силой.

При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3—4), и при Н = –H _нас достигается насыщение (точка 4). Затем фер­ромагнетик можно опять размагнитить (кривая 4—5— 6) и вновь перемагнитить до насыщения (кривая 6 — 7).

Таким образом, при действии на ферромагнетик переменного магнитного поля намагниченность J изменяется в соответствии с кривой 1 — 2 — 3 — 4—5—6—1, которая называется петлей гистерезиса (от греч. «запаздывание»). Гистерезис приводит к тому, что намагничение ферромагнетика не является однозначной функцией Н, т.е. одному и тому же значению Н соответствует несколько значений J.

Различные ферромагнетики дают разные гистерезисные петли. Ферромагнетики с малой (в пределах от нескольких тысячных до 1—2 А/см) коэрцитивной силой Нс (с узкой петлей гистерезиса) называются мягкими, с большой (от нескольких десятков до нескольких тысяч ампер на сантиметр) коэрцитивной силой (с широкой петлей гистерезиса) — жесткими. Величины Нс, J _ос и m _max определяют применимость фер­ромагнетиков для тех или иных практических целей. Taк, жесткие ферромагнетики (например, углеродистые и вольфрамовые стали) применяются для изготовления постоянных магнитов, а мягкие (например, мягкое железо, сплав железа с нике­лем) — для изготовления сердечников трансформаторов.

Ферромагнетики обладают еще одной существенной особенностью: для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик. Переход вещества из ферромагнитного состояния в парамагнитное, происходящий в точке Кюри, не со­провождается поглощением или выделением теплоты, т.е. в точке Кюри происходит фазовый переход II рода (см. § 75).

Наконец, процесс намагничения ферромагнетиков сопровождается изменением его линейных размеров и объема. Это явление получило название магнитострикции. Величина и знак эффекта зависят от напряженности Н намагничивающего поля, от природы ферромагнетика и ориентации кристаллографических осей по отношению к полю.

§ 136. Природа ферромагнетизма

Рассматривая магнитные свойства ферромагнетиков, мы не вскрывали физическую природу этого явления. Описательная теория ферромагнетизма была разработана французским физиком П. Вейссом (1865—1940). Последовательная количественная теория на основе квантовой механики развита Я. И. Френкелем и немецким физиком В. Гейзенбергом (1901—1976).

Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Спонтанное намагничение, однако, находится в кажущемся противоречии с тем, что многие ферромагнитные материалы даже при температурах ниже точки Кюри не намагничены. Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей — доменов, самопроизвольно намагниченных до насыщения.

При отсутствии внешнего магнитного поля магнитные моменты отдельных до­менов ориентированы хаотически и компенсируют друг друга, поэтому результиру­ющий магнитный момент ферромагнетика равен нулю и ферромагнетик не намаг­ничен. Внешнее магнитное поле ориентирует по полю магнитные моменты не отдель­ных атомов, как это имеет место в случае парамагнетиков, а целых областей спонтан­ной намагниченности. Поэтому с ростом Н намагниченность J (см. рис. 192) и магнит­ная индукции В (см. рис. 193) уже в довольно слабых полях растут очень быстро. Этим объясняется также увеличение m ферромагнетиков до максимального значения в слабых полях (см. рис. 194). Эксперименты показали, что зависимость B от H не является такой плавной, а имеет ступенчатый вид, как показано на рис. 193. Это свидетельствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком.

При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепловое движение не в состоянии быстро дезориен­тировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис. 195). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную силу; размаг­ничиванию способствуют также встряхивание и нагревание ферромагнетика. Точка Кюри оказывается той температурой, выше которой происходит разрушение доменной структуры.

Существование доменов в ферромагнетиках доказано экспериментально. Прямым экспериментальным методом их наблюдения является метод порошковых фигур. На тщательно отполированную поверхность ферромагнетика наносится водная суспензия мелкого ферромагнитного порошка (например, магнетита). Частицы оседают преиму­щественно в местах максимальной неоднородности магнитного поля, т. е. на границах между доменами. Поэтому осевший порошок очерчивает границы доменов и подобную картину можно сфотографировать под микроскопом. Линейные размеры доменов оказались равными 10^–4 — 10^–2 см.

Дальнейшее развитие теории ферромагнетизма Френкелем и Гейзенбергом, а также ряд экспериментальных фактов позволили выяснить природу элементарных носителей ферромагнетизма. В настоящее время установлено, что магнитные свойства ферромагнетиков определяются спиновыми магнитными моментами элект­ронов (прямым экспериментальным указанием этого служит опыт Эйнштейна и де Гааза, см. § 131). Установлено также, что ферромагнитными свойствами могут обладать только кристаллические вещества, в атомах которых имеются недостроен­ные внутренние электронные оболочки с нескомпенсированными спинами. В подо­бных кристаллах могут возникать силы, которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу, что и приводит к возникновению областей спонтанного намагничения. Эти силы, называемые обменными силами, имеют квантовую природу — они обусловлены волновыми свойствами электронов.

Так как ферромагнетизм наблюдается только в кристаллах, а они обладают анизотропией (см. § 70), то в монокристаллах ферромагнетиков должна иметь место анизотропия магнитных свойств (их зависимость от направления в кристалле). Дейст­вительно, опыт показывает, что в одних направлениях в кристалле его намагничен­ность при данном значении напряженности магнитного поля наибольшая (направление легчайшего намагничения), в других — наименьшая (направление трудного намагничения). Из рассмотрения магнитных свойств ферромагнетиков следует, что они похожи на сегнетоэлектрики (см. § 91).

Существуют вещества, в которых обменные силы вызывают антипараллельную ориентацию спиновых магнитных моментов электронов. Такие тела называются антиферромагнетиками. Их существование теоретически было предсказано Л.Д. Лан­дау. Антиферромагнетиками являются некоторые соединения марганца (MnO, MnF₂), железа (FeO, FeCl₂) и многих других элементов. Для них также существует антиферромагнитная точка Кюри (точка Нееля*), при которой магнитное упорядочение спиновых магнитных моментов нарушается и антиферромагнетик превращается в парамагнетик, претерпевая фазовый переход II рода (см. § 75).

* Л. Неель (род. 1904) — французский физик.

В последнее время большое значение приобрели полупроводниковые ферромаг­нетики — ферриты, химические соединения типа МeО×Fе₂О₃, где Me — ион двухва­лентного металла (Mn, Co, Ni, Сu, Mg, Zn, Cd, Fe). Они отличаются заметными ферромагнитными свойствами и большим удельным электрическим сопротивлением (в миллиарды раз большим, чем у металлов). Ферриты применяются для изготовления постоянных магнитов, ферритовых антенн, сердечников радиочастотных контуров, элементов оперативной памяти в вычислительной технике, для покрытия пленок в магнитофонах и видеомагнитофонах и т. д.

Задачи

16.1. Напряженность однородного магнитного поля в меди равна 10 А/м. Определить магнитную индукцию поля, создаваемого молекулярными токами, если диамагнитная восприимчи­вость меди |c|=8,8×10^–8. [1.11 пТл]

16.2. По круговому контуру радиусом 50 см, погруженному в жидкий кислород, течет ток 1,5 А. Определить намагниченность в центре этого контура, если магнитная восприимчивость жидкого кислорода 3,4×10^–3. [5,1 мА/м]

16.3. По обмотке соленоида индуктивностью 1 мГн, находящегося в диамагнитной среде, течет ток 2 А. Соленоид имеет длину 20 см, площадь поперечного сечения 10 см² и 400 витков. Определить внутри соленоида: 1) магнитную индукцию; 2) намагниченность. [1) 5 мТл; 2) 20 А/м]

16.4. Алюминиевый шарик радиусом 0,5 см помещен в однородное магнитное поле (B ₀ = 1 Тл). Определить магнитный момент, приобретенный шариком, если магнитная восприимчи­вость алюминия 2,1×10^–5. [8,75 мкА×м²]

Глава 17 Основы теории Максвелла для электромагнитного поля

§ 137. Вихревое электрическое поле

Из закона Фарадея (см. (123.2)) =–dФ/d t следует, что любое изменение сцепленного с контуром потока магнитной индукции приводит к возникновению электродвижущей силы индукции и вследствие этого появляется индукционный ток. Следовательно, возникновение э.д.с. электромагнитной индукции возможно и в неподвижном контуре,находящемся в переменном магнитном поле. Однако э.д.с. в любой цепи возникает только тогда, когда в ней на носители тока действуют сторонние силы — силы неэлектростатического происхождения (см. § 97). Поэтому встает вопрос о природе сторонних сил в данном случае.

Опыт показывает, что эти сторонние силы не связаны ни с тепловыми, ни с хи­мическими процессами в контуре; их возникновение также нельзя объяснить силами Лоренца, так как они на неподвижные заряды не действуют. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем простран­стве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. Согласно представлениям Максвелла, контур, в котором появляется э.д.с., играет второстепенную роль, являясь своего рода лишь «прибором», обнаружи­вающим это поле.

Итак, по Максвеллу, изменяющееся во времени магнитное поле порождает элект­рическое поле Е _B, циркуляция которого, по (123.3),

(137.1)

где Е_Bl — проекция вектора Е _B на направление d l.

Подставив в формулу (137.1) выражение (см. (120.2)), получим

Если поверхность и контур неподвижны, то операции дифференцирования и интег­рирования можно поменять местами. Следовательно,

(137.2)

где символ частной производной подчеркивает тот факт, что интеграл B d S является функцией только от времени.

Согласно (83.3), циркуляция вектора напряженности электростатического поля (обозначим его E _Q) вдоль любого замкнутого контура равна нулю:

(137.3)

Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми полями (E _B и Е _Q) имеется принципиальное различие: циркуляция вектора E _B в отличие от циркуляции вектора E _Q не равна нулю. Следовательно, электрическое поле E _B, возбуж­даемое магнитным полем, как и само магнитное поле (см. § 118), является вихревым.

§ 138. Ток смещения

Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружа­ющем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнит­ным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.

Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обклад­ками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (I) и смещения (I _см) равны: I _см =I.

Ток проводимости вблизи обкладок конденсатора

(138.1)

(поверхностная плотность заряда s на обкладках равна электрическому смещению D в конденсаторе (см. (92.1)). Подынтегральное выражение в (138.1) можно рассматривать как частный случай скалярного произведения когда и d S взаимно параллельны. Поэтому для общего случая можно записать

Сравнивая это выражение с (см. (96.2)), имеем

(138.2)

Выражение (138.2) и было названо Максвеллом плотностью тока смещения.

Рассмотрим, каково же направление векторов плотностей токов проводимости и смещения j и j _см. При зарядке конденсатора (рис. 197, а) через проводник, соединя­ющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе усиливается; следовательно, >0, т. е. вектор направлен в ту же сторону, что и D. Из рисунка видно, что направления векторов и j совпадают. При разрядке конденсатора (рис. 197, б) через проводник, соединяющий обкладки, ток течет от левой обкладки к правой; поле в конденсаторе ослабляется; следовательно, <0, т. е. вектор направлен противоположно вектору D. Однако вектор направлен опять так же, как и вектор j. Из разобранных примеров следует, что направление вектора j, а следовательно, и вектора j _см, совпадает с направлением вектора , как это и следует из формулы (138.2).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Макс­велл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 197 штриховыми линиями).

В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D =e₀ E + P, где Е – напряженность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения

(138.3)

Поиск по сайту: