Тангенциальная составляющая ускорения 19 страница

На заряд Q ₀ помимо сторонних сил действуют также силы электростатического поля F _e= Q ₀ E. Таким образом, результирующая сила, действующая в цепи на заряд Q ₀, равна

Работа, совершаемая результирующей силой над зарядом Q ₀ на участке 1 — 2, равна

Используя выражения (97.3) и (84.8), можем записать

(97.4)

Для замкнутой цепи работа электростатических сил равна нулю (см. § 83), поэтому в данном случае

Напряжением U на участке 1 — 2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторон­них сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),

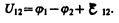
Понятие напряжения является обобщением понятия разности потенциалов: напря­жение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует Э.д.с., т. е. сторонние силы отсутствуют.

§ 98. Закон Ома. Сопротивление проводников

Немецкий физик Г. Ом (1787;—1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

(98.1)

где R — электрическое сопротивление проводника. Уравнение (98.1) выражает закон Ома для участка цепи (не содержащего источника тока): сала тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротив­лению проводника. Формула (98.1) позволяет установить единицу сопротивления — ом (Ом): 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина

называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом.

Сопротивление проводников зависит от его размеров и формы, а также от матери­ала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

(98.2)

где r — коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного элект­рического сопротивления — ом×метр (Ом×м). Наименьшим удельным сопротивлением обладают серебро (1,6×10^–8 Ом×м) и медь (1,7×10^–8 Ом×м). На практике наряду с медными применяются алюминиевые провода. Хотя алюминий и имеет большее, чем медь, удельное сопротивление (2,6×10^–8 Ом×м), но зато обладает меньшей плотностью по сравнению с медью.

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (98.2) в закон Ома (98.1), получим

(98.3)

где величина, обратная удельному сопротивлению,

называется удельной электрической проводимостью вещества проводника. Ее едини­ца — сименс на метр (См/м). Учитывая, что U / l = Е — напряженность электрического поля в проводнике, I/S = j — плотность тока, формулу (98.3) можно записать в виде

(98.4)

Так как в изотропном проводнике носители тока в каждой точке движутся в направле­нии вектора Е, то направления j и Е совпадают. Поэтому формулу (98.4) можно записать в виде

(98.5)

Выражение (98.5) — закон Ома в дифференциальном форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:

где r и r ₀, R и R ₀ — соответственно удельные сопротивления и сопротивления провод­ника при t и 0°С, a — температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К^–1. Следовательно, температур­ная зависимость сопротивления может быть представлена в виде

где Т — термодинамическая температура.

Качественный ход температурной зависимости сопротивления металла представлен на рис. 147 (кривая 1). Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах T_K (0,14—20 К), называемых критическими, характерных для каждого вещества, скачко­образно уменьшается до нуля (кривая 2), т. е. металл становится абсолютным провод­ником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов (в об­мотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуют­ся керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.

На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления, которые позволяют по градуированной взаимо­связи сопротивления от температуры измерять температуру с точностью до 0,003 К. Термометры сопротивления, в которых в качестве рабочего вещества используются полупроводники, изготовленные по специальной технологии, называются термисторами. Они позволяют измерять температуры с точностью до миллионных долей кельвин.

§ 99. Работа и мощность тока. Закон Джоуля — Ленца

Рассмотрим однородный проводник, к концам которого приложено напряжение U. За "время d t через сечение проводника переносится заряд d q=I d t. Так как ток представляет собой перемещение заряда d q под действием электрического поля, то, по формуле (84.6), работа тока

(99.1)

Если сопротивление проводника R, то, используя законОма (98.1), получим

(99.2)

Из (99.1) и (99.2) следует, что мощность тока

(99.3)

Если сила тока выражается в амперах, напряжение — в вольтах, сопротивле­ние — в омах, то работа тока выражается в джоулях, а мощность — в ваттах. На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1 Вт×ч — работа тока мощностью 1 Вт в течение 1 ч; 1 Вт×ч=3600 Bт×c=3,6×10³ Дж; 1 кВт×ч=10³ Вт×ч= 3,6×10⁶ Дж.

Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,

(99.4)

Таким образом, используя выражения (99.4), (99.1) и (99.2), получим

(99.5)

Выражение (99.5) представляет собой закон Джоуля — Ленца, экспериментально уста­новленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.*

* Э. X. Ленц (1804—1865) — русский физик.

Выделим в проводнике элементарный цилиндрический объем d V= d S d l (ось цилин­дра совпадает с направлением тока), сопротивление которого По закону Джоуля — Ленца, за время d t в этом объеме выделится теплота

Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна

(99.6)

Используя дифференциальную форму законаОма (j=gЕ) и соотношение r= 1 /g, получим

(99.7)

Формулы (99.6) и (99.7) являются обобщенным выражением закона Джоуля—Ленца в дифференциальной форме, пригодным для любого проводника.

Тепловое действие тока находит широкое применение в технике, которое началось с открытия в 1873 г. русским инженером А. Н. Лодыгиным (1847—1923) лампы накаливания. На нагревании проводников электрическим током основано действие элект­рических муфельных печей, электрической дуги (открыта русским инженером В. В. Петровым (1761—1834)), контактной электросварки, бытовых электронагрева­тельных приборов и т. д.

§ 100. Закон Ома для неоднородного участка цепи

Мы рассматривали закон Ома (см. (98.1)) для однородного участка цепи, т. е. такого, в котором не девствует э.д.с. (не действуют сторонние силы). Теперь рассмотрим неоднородный участок цепи, где действующую э.д.с. на участке 1 — 2 обозначим через а приложенную на концах участка разность потенциалов — через j ₁ —j ₂.

Если ток проходит по неподвижным проводникам, образующим участок 1—2, то работа А ₁₂ всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда Q ₀ на участке 1 — 2, согласно (97.4),

(100.1)

Э.д.с. как и сила тока I, — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если э.д.с. способствует движению положительных зарядов в выбранном направлении (в направлении 1—2), то 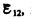> 0. Если э.д.с. препятствует движению положительных зарядов в данном направлении, то < 0. За время t в проводнике выделяется теплота (см. (99.5))

(100.2)

Из формул (100.1) и (100.2) получим

(100.3)

откуда

(100.4)

Выражение (100.3) или (100.4) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует ( =0), то из (100.4) приходим к закону Ома для однородного участка цепи (98.1):

(при отсутствии сторонних сил напряжение на концах участка равно разности потенци­алов (см. § 97)). Если же электрическая цепь замкнута, то выбранные точки 1 и 2 со­впадают, j ₁= j ₂; тогда из (100.4) получаем закон Ома для замкнутой цепи:

где 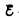- э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае R=r+R ₁, где r — внутреннее сопротивление источника тока, R ₁ — со­противление внешней цепи. Поэтому законОма для замкнутой цепи будет иметь вид

Если цепь разомкнута и, следовательно, в ней ток отсутствует (I = 0), то из закона Ома (100.4) получим, что =j ₁ —j ₂, т. е. э.д.с., действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Следовательно, для того чтобы найти э.д.с. источника тока, надо измерить разность потенциалов на егоклеммах при разомкнутой цепи.

§ 101. Правила Кирхгофа для разветвленных цепей

Обобщенный закон Ома (см. (100.3)) позволяет рассчитать практически любую слож­ную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколь­ко замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т. д.), довольно сложен. Эта задача решает­ся более просто с помощью двух правил Кирхгофа. *

*Г. Кирхгоф (1824—1887) — немецкий физик.

Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Например, для рис. 148 первое правило Кирхгофа запишется так:

Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке провод­ника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.

Второе правило Кирхгофа получается из обобщенного закона Ома для разветвлен­ных цепей. Рассмотрим контур, состоящий из трех участков (рис. 149). Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с напра­влением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома (100.3), можно записать:

Складывая почленно эти уравнения, получим

(101.1)

Уравнение (101.1) выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме э.д.с., встречающихся в этом контуре:

(101.2)

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.

2. Выбрать направление обхода контура и строго его придерживаться; произведе­ние IR положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются поло­жительными, против — отрицательными.

3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматрива­емой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных.

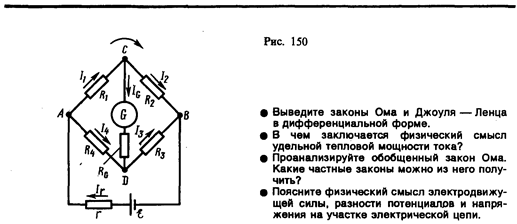
В качестве примера использования правил Кирхгофа рассмотрим схему (рис. 150) измеритель­ного моста Уитстона. * Сопротивления R ₁, R ₂, R ₃и R ₄ образуют его «плечи». Между точками А и В моста включена батарея с э.д.с. 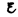и сопротивлением r, между точками С и D включен гальванометр с сопротивлением R_G. Для узлов А, В и С, применяя первое правило Кирхгофа, получим

(101.3)

Для контуров АСВA, ACDA и CBDC, согласно второму правилу Кирхгофа, можно записать:

(101.4)

* Ч. Уитстон (1802—1875) — английский физик.

Если известны все сопротивления и э.д.с., то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления R ₂, R ₃ и R ₄, можно добиться того, чтобы ток через гальванометр был равен нулю (I_G = 0). Тогда из (101.3) найдем

(101.5)

а из (101.4) получим

(101.6)

Из (101.5) и (101.6) вытекает, что

(101.7)

Таким образом, в случае равновесного моста (I_G = 0) при определении искомого сопротивления R ₁ э.д.с. батареи, сопротивления батареи и гальванометра роли не играют.

На практике обычно используется реохордный мост Уитстона (рис. 151), где сопротивле­ния R ₃и R ₄ представляют собой длинную однородную проволоку (реохорд) с большим удельным сопротивлением, так что отношение R ₃ /R ₄ можно заменить отношением l ₃/ l ₄. Тогда, используя выражение (101.7), можно записать

(101.8)

Длины l ₃ и l ₄ легко измеряются по шкале, a R ₂ всегда известно. Поэтому уравнение (101.8) позволяет определить неизвестное сопротивление R ₁.

Задачи

12.1. По медному проводнику сечением 1 мм² течет ток; сила тока 1 А. Определить среднюю скорость упорядоченного движения электронов вдоль проводника, предполагая, что на каждый атом меди приходится один свободный электрон. Плотность меди 8,9 г/см³. [74 мкм/с]

12.2. Определить, во сколько раз возрастет сила тока, проходящего через платиновую печь, если при постоянном напряжении на зажимах ее температура повышается от t ₁=20°C до t ₂=1200°С. Температурный коэффициент сопротивления платины принять равным 3,65×10^–3 К^–1. [В 5 раз]

12.3. По медному проводу сечением 0,3 мм² течет ток 0,3 А. Определить силу, действую­щую на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление меди 17 нОм×м. [2,72×10^–21 Н]

12.4. Сила тока в проводнике сопротивлением 10 Ом равномерно убывает от I ₀=3 А до I =0 за 30 с. Определить выделившееся за это время в проводнике количество теплоты. [900 Дж].

12.5. Плотность электрического тока в алюминиевом проводе равна 5 А/см². Определить удель­ную тепловую мощность тока, если удельное сопротивление алюминия 26 нОм×м. [66 Дж/(м³×с)]

12.6. Определить внутреннее сопротивление r источника тока, если во внешней цепи при силе тока I ₁=5 А выделяется мощность P ₁=10 Вт, а при силе тока I ₂=8 А — мощность P ₂=12 Вт. [0,17 Ом]

12.7. Три источника тока с э.д.с. E ₁=1,8 В, E ₂=1,4 В и E ₃=1,1 В соединены накоротко одно­именными полюсами. Внутреннее сопротивление первого источника r ₁=0,4 Ом, второ­го — r ₂=0,6 Ом. Определить внутреннее сопротивление третьего источника, если через первый источник идет ток I ₁=1,13 A. [0,2 Ом]

Глава 13 Электрические токи в металлах, вакууме и газах

§ 102. Элементарная классическая теория электропроводности металлов

Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости метал­лов, созданной немецким физиком П. Друде (1863—1906) и разработанной впоследст­вии нидерландским физиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории.

Первый из таких опытов — опыт Рикке * (1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, Аl, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (»3,5×10⁶ Кл), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856—1940) электроны.

*К. Рикке (1845—1915) — немецкий физик.

Для доказательства этого предположения необходимо было определить знак и ве­личину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед,как смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат российским физикам С. Л. Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947). Эти опы­ты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881—1948) и ранее шотландским физиком Б. Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах имеют отрицательный заряд, а их удельный заряд приблизительно одинаков для всех исследованных метал­лов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали. Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны.

Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атом­ными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электро­ны, образуя своеобразный электронный газ, обладающий, согласно электронной те­ории металлов, свойствами идеального газа.

Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По теории Друде—Лоренца, электроны обладают такой же энергией теплового движения,как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории (см. (44.3)), можно найти среднюю скорость теплового движения электронов

которая для T =300 К равна 1,1×10⁵ м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.

При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость á v ñ упорядоченного движения электронов мож­но оценить согласно формуле (96.1) для плотности тока: j = пe á v ñ. Выбрав допустимую плотность тока, например для медных проводов 10⁷ А/м², получим, что при концент­рации носителей тока n = 8×10²⁸м^–3 средняя скорость á v ñ упорядоченного движения электронов равна 7,8×10^–4 м/с. Следовательно, á v ñ<<á u ñ, т. е. даже при очень боль­ших плотностях тока средняя скорость упорядоченного движения электронов, обуслов­ливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость á v ñ + á u ñ можно заменять скоростью теплового движения á u ñ.

Казалось бы, полученный результат противоречит факту практически мгновенной передачи электрических сигналов на большие расстояния. Дело в том, что замыкание электрической цепи влечет за собой распространение электрического поля со скоро­стью с (c =3×10⁸м/с). Через время t = l / c (l — длина цепи) вдоль цепи установится стационарное электрическое поле и в ней начнется упорядоченное движение электро­нов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.

§ 103. Вывод основных законов электрического тока в классической теории электропроводности металлов

1. Закон Ома. Пусть в металлическом проводнике существует электрическое поле напряженностью E =const. Co стороны поля заряд е испытывает действие силы F = eE и приобретает ускорение a=F/m=eE/m. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость

Поиск по сайту: