 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 5. Накопление денежной единицы за период
Фактор накопления денежной единицы за период показывает какой по истечении n интервалов будет стоимость серии n известных равных сумм если каждую сумму кладут на депозит в конце интервала.
Ден.Ед
Поток известных n платежей
PMT+% Неизвестное количество
Будущей суммы
PMT
PMT
Для упрощения вывода формулы предположим, что платеж PMT = 1 денежной единице
Ден.Ед
Поток известных n платежей
PMT+% Неизвестное количество
Будущей суммы
PMT
PMT
Чтобы вывести формулу необходимо:
1) Оценить будущую стоимость каждого платежа отдельно
2) Найти сумма этих платежей.
Начнем с конца:
1-платеж = 1
2-платеж = FV=(1+i)1 =1+i
3-платеж = FV=(1+i)2
C начала:
1- платеж = FV=(1+i)i-1
2- платеж FV=(1+i)n-2
Получилась геометрическая прогрессия со знаменателем q=1+i
Сумм членов прогрессии Будущая стоимость =(an*q-a1)/(q-1)= 
Это при платеже в 1-единицу, если платеж не одна единица, то
FV=PMT* 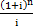
Вопрос 6: Функция фактора фонда возмещения.
Функция фактора фонда возмещения отвечает на вопрос каким должен быть периодический платеж, который происходит в конце каждого из n интервалов чтобы накопить известную сумму.
Данный случай является обратным предыдущему, то есть нам известна сумма, которую необходимо накопить, а нам нужно рассчитать платеж, который необходимо вносить на депозит в конце каждого из n периодических интервалов. Для расчета суммы платежа выражаем его из формулы: FV=PMT* 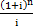
Получим, что PMT= 
Таким образом мы рассмотрели 6 функций сложного процента. Из них можно выделить три пары функций, которые являются взаимообратными по отношению друг к другу:
| Накопление | Дисконтирование |
| Взнос на амортизацию денежной единицы | Текущая стоимость аннуитета |
| Накопление денежной единицы за период | Фактор фонда возмещения |
Каждая из этих функций содержит так называемый коэффициент приращения(начисления процентов) = 
Все перечисленные функции можно рассчитать:
1) По формулам
2) По финансовым калькуляторам для фин. Расчетов.
3) По специальным таблицам. В них рассчитаны факторы сложного процента, которые не зависят от платежей, суммы кредита и т.д. Они зависят только от количества лет и ставки дохода на капитал. Они рассчитаны для величин процентов 6% - 30% и до 40-ка лет.
4) С помощью функций в экселе, которые называются << Финансовые>>
Поиск по сайту: