Наприклад, це може бути розклад гідроген йодиду

2НІ ® Н₂ + І₂

Будемо характеризувати концентрацію з допомогою N - кількості певних молекул в одиниці об’єму суміші, а швидкість реакції - кількістю молекул, що утворились або прореагували в одиниці об’єму за одиницю часу.

Скористаємось рівнянням молекулярно-кінетичної теорії газів. Число зіткнень всіх N молекул, що знаходяться в одиниці об’єму газу, за одну секунду рівна

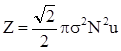, (ХІ.11.1)

де σ - ефективний діаметр молекули. Середня арифметична швидкість молекул

, (ХІ.11.2)

де М - молярна маса. Тому

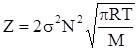(ХІ.11.3)

За законом Больцмана визначаємо число активних зіткнень, в яких енергія перевищує енергію активації:

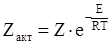(ХІ.11.4)

В результаті кожного активного зіткнення витрачається дві молекули вихідної речовини, а тому кількість прореагованих молекул в одиниці об’єму за 1 с, тобто швидкість реакції, рівна подвоєному числу активних зіткнень за цей же час і в тому ж об’ємі

. (ХІ.11.5)

Формула для швидкості одержується після підстановки загального числа зіткнень Z у вираз для числа активних зіткнень:

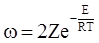, (ХІ.11.6)

або

. (ХІ.11.7)

Звідсіля видно, що швидкість реакції залежить від квадрату концентрації

, (ХІ.11.8)

де

(ХІ.11.9)

Величина k, очевидно, має зміст константи швидкості, оскільки k рівна швидкості реакції при N = 1.

Виходячи з (ХІ.11.6) і (ХІ.11.8) рівняння для константи швидкості можна записати так:

(ХІ.11.10)

Співставляючи це рівняння з рівнянням Арреніуса (ХІ.9.10), можна встановити фізичний зміст передекспоненціального множника k₀, який виявляється пропорційним загальному числу зіткнень всіх молекул в одиниці об’єму за одиницю часу. У випадку одиничної концентрації (N = 1) величина k₀ відрізняється від Z лише коефіцієнтом 2. Можна показати, що для бімолекулярних реакцій типу А + В ® Р цей коефіцієнт рівний 1. З цієї причини рівняння Арреніуса часто пишуть у вигляді:

, (ХІ.11.11)

де Z - число зіткнень молекул в одиниці об’єму за одиницю часу.

Величина Е, що входить в рівняння теорії активних зіткнень, називається істинною енергією активації на відміну від дослідної або ефективної, що визначається за рівнянням Арреніуса (ХІ.9.10).

Зв’язок між ефективною енергією активації Е _а і істинною виражається таким рівнянням

(ХІ.11.12)

Таким чином, істинна й ефективна енергія активації не цілком відповідають одна одній. Вони відрізняються на середню енергію теплового руху молекул.

Оскільки з дослідних даних слідує, що Е _а - величина стала, то передбачається, що другий член правої частини (ХІ.11.12) значно менший першого. В такому випадку зміна температури може настільки мало позначатися на зміні Е _а, що практично це не буде виявлятися. Тому вважається, що Е >> ½ RТ, а Е _а ≈ Е.

Користуючись теорією активних зіткнень, можна розрахувати числові значення константи швидкості реакції. Для деяких простих реакцій, що протікають у газах і розчинах, спостерігаються задовільні співвідношення розрахованих значень з дослідними. Гарне співвідношення, наприклад, відмічається для газової реакції розкладу гідроген йодиду, а також для реакції його синтезу. Однак, у більшості випадків спостерігається значне розходження розрахованих значень швидкостей реакцій з дослідними. Такі відхилення можна пояснити, передбачивши, що реагують лише молекули, які орієнтовані при зіткненнях певним чином. Тому з загального числа ефективних зіткнень, розрахованих за теорією, слід вважати дійсно ефективними лише деяку частину. За цією ж причиною вираз для константи швидкості записують так:

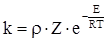, (ХІ.11.13)

де ρ - так званий стеричний фактор або фактор імовірності.

Вважається, що стеричний фактор відрізняється від одиниці не лише тому, що для здійснення реакції необхідна певна орієнтація реагуючих молекул, а і залежністю імовірності реакції від часу взаємодії цих молекул у момент зіткнення. В тих випадках, коли зіткнення відбувається занадто швидко, молекули не встигають прореагувати.

Поняття стеричного фактора, проте, не завжди достатньо добре відповідає дослідним даним. Зустрічаються реакції, для яких величина ρ більша одиниці або занадто мала (порядку 10^-8), що важко пояснити. Теорія не в змозі розрахувати величину ρ. Всі ці недоліки пов’язані з недосконалістю і формальним характером теорії активних зіткнень, що уявляє молекули реагуючих речовин у вигляді твердих кульок. З термодинамічних міркувань випливає, що стеричний фактор повинен бути пов’язаний зі зміною ентропії в ході реакції, що також не пояснюється теорією зіткнень.

Поиск по сайту: