ХІ.7.Складні реакції

Кінетика складних реакцій залежить від форми зв’язку між простими реакціями, від співвідношення їх швидкостей і базується на принципі незалежності простих реакцій. Згідно з цим принципом, якщо в системі протікають одночасно декілька реакцій, то кожна з них незалежна від інших і її швидкість визначається кінетичними рівняннями простих реакцій.

Швидкість реакції, що складається з ряду послідовних стадій, визначається в основному швидкістю стадії, що має найменшу константу швидкості. Така стадія називається визначаючою або лімітуючою. Виведення кінетичного рівняння лімітуючої стадії є однією з найбільш практичних задач кінетичного дослідження.

До складних реакцій відносять оборотні (двохсторонні), паралельні, послідовні (консекутивні), автокаталітичні, спряжені і їх поєднання. Ці реакції можуть підкоряться кінетичним закономірностям реакцій першого, другого і, в принципі, інших порядків так як і прості реакції. Обмежимось розглядом складних реакцій, що складаються з реакцій першого порядку.

1. Оборотні (двохсторонні) реакції. Оборотними називають реакції, що протікають одночасно в двох протилежних напрямках. Швидкість реакції рівна різниці швидкостей прямої і зворотної реакцій.

Розглянемо оборотну реакцію першого порядку типу

k_А

А В

k_В

Прикладом такого процесу може служити ізомеризація нормальних вуглеводнів, наприклад, н-бутана в ізобутан.

Внаслідок прямої реакції концентрація речовини В зростає, а внаслідок зворотної - падає.

Виберемо відлік часу так, щоб у початковий момент часу, при t = 0, існувала лише вихідна речовина, а концентрація продукту була рівна нулю.

Врахуємо, що в даній реакції зниження певної кількості молекул вихідної речовини викликає утворення точно такої ж кількості молекул продуктів реакції, а тому сума концентрацій обох реагентів у ході реакції не змінюється:

с_А + х = а, (ХІ.7.1)

де а - початкова концентрація вихідної речовини; х - концентрація продукту В в момент часу t.

Нехай dx = dx₁ + dx₂, де dx₁ і dx₂ - зміна концентрації продукту реакції в прямій і зворотній реакціях відповідно. У випадку рівноваги швидкості прямого і зворотного процесів рівні:

, (ХІ.7.2)

а тому

, (ХІ.7.3)

де х_р - концентрація продукту реакції в стані рівноваги.

Запишемо кінетичне рівняння прямої і зворотної стадій, використовуючи концентрацію речовини В:

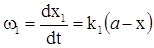; (ХІ.7.4)

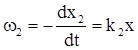(ХІ.7.5)

Знаходимо швидкість сумарної реакції

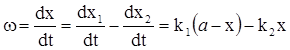(ХІ.7.6)

або

. (ХІ.7.7)

Потім

. (ХІ.7.8)

Після інтегрування отримаємо рівняння:

(ХІ.7.9)

і

. (ХІ.7.10)

Враховуючи (ХІ.7.3), маємо:

, (ХІ.7.11)

звідки

(ХІ.7.12)

і

. (ХІ.7.13)

Рівняння (ХІ.7.11) і (ХІ.7.13) показують, що двохсторонні реакції з мономолекулярними стадіями протікають за законами односторонніх мономолекулярних реакцій, у яких k = (k₁ + k₂) і а = х_р.

З умов рівноваги (ХІ.7.3), (ХІ.7.11) знаходимо

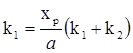(ХІ.7.14)

і

. (ХІ.7.15)

Віднімаючи від рівняння (ХІ.7.11) рівняння (ХІ.7.15) визначимо k₂

, (ХІ.7.16)

звідкіля

(ХІ.7.17)

Таким чином, основні характеристики двосторонніх реакцій можна одержати, знаючи концентрації реагентів в початковий і довільний момент часу, а також х_р, або константу рівноваги К_с = k₁/k₂. Зв’язок К_р і К_с визначають рівнянням (ХІ.7.3), з якого, після того, як розділимо обидві частини на k₂, одержуємо

К_с а = (К_с + 1)х_р, (ХІ.7.18)

звідкіля

(ХІ.7.19)

2. Паралельні реакції. Паралельними називають реакції, що протікають одночасно за декількома напрямками з утворенням різних продуктів. До таких реакцій, наприклад, відноситься реакція розкладу бертолетової солі

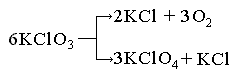
Розглянемо в загальному вигляді найбільш простий випадок паралельних реакцій

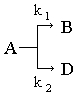
коли є дві мономолекулярні стадії, що одночасово перебігають кожна з яких перебігає за першим порядком. В більш складних випадках таких стадій може бути і більше, а їх порядок може відрізнятися від одиниці.

Позначимо через k₁ і k₂ константи швидкості цих стадій і виберемо відлік часу так, щоб при t = 0 концентрації продуктів с_В,0 = с_D,0 = 0. Покладемо с_А,0 = а, с_А = а - х, с_В = х₁, с_D = х₂.

Кінетичні рівняння окремих стадій такі:

(ХІ.7.20)

і

. (ХІ.7.21)

Швидкість сумарної реакції

. (ХІ.7.22)

З рівняння реакції витікає, що число молекул продуктів В і D рівні числу вихідних молекул А, що розпадаються, тобто х = х₁ + х₂.

Тому

(ХІ.7.23)

Значить, для паралельної реакції, стадії якої значно відрізняються за швидкістю, визначною є більш швидка стадія. Наприклад, якщо w₁ >> w₂, то w ≈ w₁.

Підставляючи w₁ і w₂ з рівнянь (ХІ.7.20) і (ХІ.7.21) в рівняння (ХІ.7.23)

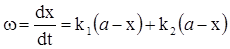, (ХІ.7.24)

звідкіля

(ХІ.7.25)

Після інтегрування одержимо

. (ХІ.7.26)

Тому

; (ХІ.7.27)

; (ХІ.7.28)

. (ХІ.7.29)

Зробивши ряд перетворень, одержуємо, що

(ХІ.7.30)

і

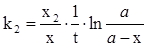(ХІ.7.31)

Таким чином, за допомогою одержаних з досліду концентрацій продуктів можна визначити константу швидкості і кінетичний закон окремих стадій паралельної реакції.

3. Послідовні реакції. Послідовними реакціями називаються реакції з проміжними стадіями. При таких реакціях проміжний продукт, що утворюється, далі витрачається на наступні стадії. Послідовною, наприклад, є реакція гідролізу трисахаридів у кислому середовищі:

С₁₈Н₃₂О₁₆ + Н₂О ® С₆Н₁₂О₆ + С₁₂Н₂₂О₁₁

Розглянемо реакцію, що складається з двох простих мономолекулярних стадій:

k₁ k₂

A → B → C

Припустимо, що в початковий момент часу t = 0 концентрація речовини А рівна а; концентрації речовин В і С рівні нулю. Нехай на момент часу t в одиниці об’єму прореагує х молей речовин А; нехай у з них перетворилися в речовину С. Таким чином, на цей момент концентрація речовини А = а -х; концентрація речовини В = х-у; концентрація речовини С = у.

Швидкість хімічної реакції за кожною з цих речовин рівна

; (ХІ.7.32)

; (ХІ.7.33)

. (ХІ.7.34)

Після інтегрування рівняння (ХІ.7.32) будемо мати:

(ХІ.7.35)

Підставимо це рівняння в рівняння (ХІ.7.33) і введемо позначення х - у = z. Тоді

(ХІ.7.36)

або

(ХІ.7.37)

Це лінійне неоднорідне диференційне рівняння. Відомо, що метод його розв’язку полягає в тому, що спочатку розв’язують відповідне однорідне рівняння, а потім, варіюючи довільну сталу, знаходять розв’язок неоднорідного рівняння. Внаслідок такого розв’язку для проміжної речовини

. (ХІ.7.38)

Збільшення концентрації продукту з часом виражатиметься рівнянням

. (ХІ.7.39)

Послідовна реакція протікає так, щоконцентрація вихідної речовини монотонно зменшується за експонціальним законом (рис. 59).

Концентрація проміжної речовини проходить через максимум. Кінцева речовина утворюється спочатку повільно, а потім швидкість зростає, що є причиною перегину кривої у на початку протікання процесу.

В загальному швидкість багатостадійної послідовної реакції буде визначатись швидкістю найбільш повільної реакції.

Точний розгляд кінетики складної реакції пов’язаний з розв’язком диференційних рівнянь. При збільшенні числа стадій і для більш високих порядків стадій математичні складності сильно зростають. Тому стають доцільними наближені методи. До їх числа відноситься метод стаціонарних концентрацій Боденштейна, що придатний для розгляду стаціонарного протікання процесів, у яких утворюються проміжні речовини, які вступають у подальшу взаємодію так швидко, що їх концентрації в ході процесу залишаються практично сталими. Ця умова дозволяє перейти до розгляду алгебраїчних рівнянь замість диференціальних, що суттєво спрощує розв’язок. Для прикладу повернемось до послідовної реакції

k₁ k₂

A → B → C

Нехай k₂>k₁, і проміжна речовина швидко розпадається. Будемо вважати, що максимум кривої (х-у) = f (t) (рис. 59) достатньо широкий і розтягнутий в часі. Тоді, нехтуючи в рівнянні (ХІ.7.38) k₁ y порівнянні з k₂ і y порівнянні з , одержуємо

(ХІ.7.40)

Для того, щоб одержати математичний вираз для концентрації проміжної речовини даної реакції методом стаціонарних концентрацій, необхідно прийняти, що число молекул проміжної речовини, які утворюються і розпадаються, однакові, а значить швидкості їх утворення і розпаду рівні.

Прирівнявши і , одержуємо

(ХІ.7.41)

Але за рівнянням (ХІ.7.35) і тому

. (ХІ.7.42)

4. Автокаталітичні реакції. Відомі випадки, коли продукти реакції впливають на її швидкість. Реакції, що прискорюються утвореними продуктами, називаються автокаталітичними або такими, що самоприскорюються. Найпростішим прикладом є необоротна автокаталітична реакція першого порядку.

(ХІ.7.43)

Функція (а -х)х проходить через симетричний максимум при х = а /2. У відповідності з цим швидкість процесу спочатку зростає, проходить через максимум при а /2 і потім спадає до нуля, коли вичерпуються вихідні речовини. Перетворюючи (ХІ.7.43), одержуємо:

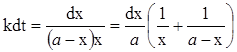(ХІ.7.44)

Проінтегруємо це рівняння:

(ХІ.7.45)

Зменшення швидкості реакції під впливом її продуктів називається гальмуванням продуктами, а реакції такого типу називаються такими, що самогальмуються:

(ХІ.7.46)

5. Спряжені реакції. Багато хімічних реакцій протікають за участю активних нестійких проміжних речовин - атомів, радикалів тощо. З цим пов’язане відкриття явища хімічної індукції, яке полягає в одночасному протіканні таких реакцій, одна з яких протікає лише в присутності другої:

А + В ® М (а)

А + С ® N (б)

Так, реакція (а) протікає лише сумісно з іншою, тобто вона індукується останньою (б). В таких випадках речовина С слугує індуктором першої реакції. Прикладом таких реакцій може служити окиснення заліза сульфату і йодидної кислоти пероксидом водню. Залізо сульфат окиснюється незалежно від того, чи присутня йодидна кислота, остання ж в чистому вигляді пероксидом водню не окиснюється, але якщо йде процес окиснення заліза сульфату, то присутня йодидна кислота теж буде окиснюватися. Речовину А, загальну для двох реакцій (пероксид водню), називають актором, речовину В - акцептором, а речовину С - індуктором.

Сутність явища хімічної індукції полягає у тому, що утворення високореакційноздатних проміжних продуктів у первинних реакціях супроводжується значним зменшенням енергії Гельмгольца (ΔА<0), забезпечує можливість протікання інших (індукованих) реакцій, у тому числі навіть таких, що супроводжуються збільшенням такої енергії (∆А>0), протікання яких стає можливим дякуючи участі активних проміжних продуктів. Спряжені реакції відіграють надзвичайно важливу роль у біології, оскільки утворення білків і нуклеїнових кислот протікає зі збільшенням енергії Гельмгольца, іде спряжено з реакцією гідролізу аденозинтрифосфорної кислоти (АТФ), що супроводжується зменшенням енергії Гельмгольца (ΔА<0) і є джерелом енергії для різноманітних хімічних процесів в клітинах.

Кінетика спряжених реакцій описується системою нелінійних рівнянь.

Поиск по сайту: