ХІ.6. Визначення порядку і константи швидкості реакції

Знаходження порядку реакції сприяє виясненню її механізму. Розрізняють частковий і загальний порядки реакції. Частковим називають порядок, що визначається за зміною концентрації однієї з речовин, яка вступає в реакцію. Сума часткових порядків дає загальний порядок реакції.

Частковий порядок знаходять декількома методами. Найбільш простий метод підстановок полягає в тому, що підставляють експериментальні дані с = f(t) у кінцеві рівняння різних порядків і знаходять, яке з них дає сталу величину константи швидкості. Наприклад, якщо провести реакції омилення ефіру лугом і підставити час і концентрації в рівняння першого порядку, то k не буде сталою величиною (0,089; 0,077; 0,060; 0,050; 0,039). Якщо ж ці дані підставити в рівняння реакції другого порядку, то значення k буде практично сталою (0,0070; 0,0067; 0,0069; 0,0066; 0,0066). Таким чином, реакція омилення ефіру лугом є реакцією другого порядку.

Методи визначення порядку, а також і константи швидкості можуть бути як інтегральними, коли в основу визначення кладеться ступінь перетворення, що досягається за даний час, так і диференціальними, коли виходять із величини швидкості реакції в різні моменти часу. Якщо одночасно невідомі як порядок, так і константи швидкості реакції, найбільш зручним є графічний метод, заснований на рівнянні (ХІ.5.11):

(ХІ.6.1)

Будуючи графік lnw ¸ lnc (рис. 57), одержуємо пряму, тангенс кута нахилу якої рівний n = tgα, а відрізок, що відтинається на вісі ординат, рівний lnk.

Цей прийом забезпечує достатньо надійне встановлення величини порядку реакції. Знайшовши величину порядку реакції, можна обчислити величину константи швидкості за рівняннями (ХІ.4.7), (ХІ.5.4), (ХІ.5.6), (ХІ.5.9), (ХІ.5.12).

Проводять також визначення константи швидкості і порядку реакції, будуючи графіки за дослідними даними в різних координатах в залежності від порядку реакції за речовиною. Так, якщо рівняння (ХІ.4.9) прологарифмувати, то воно набуде вигляду

lnc = ln c₀ - kt. (ХІ.6.2)

Рівняння (ХІ.5.1) (при умові рівності концентрацій вихідних речовин), можна привести до виду, зробивши відповідні перетворення,

, (ХІ.6.3)

а рівняння (ХІ.5.8), зробивши також відповідні перетворення, запишемо так

(ХІ.6.4)

Як видно з рівнянь (ХІ.6.2), (ХІ.6.3) і (ХІ.6.4), графіки, побудовані за дослідними даними для концентрацій вихідних речовин, що розглядаються в різні моменти часу протікання реакції, будуть задаватись прямою лінією: якщо це реакції першого порядку то в координатах lnc¸t, при n = 2 - в координатах ; а при n = 3 - в координатах .

Якщо, наприклад, графік, побудований за дослідними даними, виявиться прямолінійним на графіку в координатах , то це означає, що порядок реакції за речовиною, що розглядається складає два. Окрім цього за тангенсом кута нахилу такої прямої можна визначити константу швидкості реакції.

Зручно визначати порядок реакції за часом напівперетворення. Для цього слід провести декілька дослідів, взявши кожний раз однакову концентрацію даної речовини, і вияснити, як залежить час напіврозпаду від концентрації вихідної речовини. Як слідує з рівняння (ХІ.5.13) час напіврозпаду обернено пропорційний концентрації вихідної речовини в степені на одиницю меншій, ніж порядок реакції. Це означає, що вивчаючи експериментально залежність часу напіврозпаду від початкової концентрації вихідної речовини, можна визначити порядок реакції. Логарифмуючи вираз (ХІ.5.13), одержимо

(ХІ.6.5)

В координатах lg t = f(lg a) це рівняння описує пряму (рис. 58).

Відрізок, що відсікається цією прямою на вісі ординат, рівний 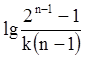, а тангенс кута φ нахилу прямої (tgφ = -n+1) визначає порядок реакції

. (ХІ.6.6)

Порядок реакції можна визначати за методом Вант-Гоффа. В перші моменти реакції можна вважати, що а -х ≈ а. Тоді кінетичне рівняння матиме вигляд 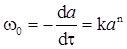, де n - порядок реакції, w₀ - початкова швидкість реакції. Проводяться два досліди, в яких початкові концентрації речовини, за якою визначається порядок реакції, рівні а ₁ і а ₂ (концентрації інших речовин у багато разів більші). Тоді швидкості реакції у першому і другому дослідах будуть:

; . (ХІ.6.7)

Поділимо ці рівняння одне на одне, прологарифмуємо і знайдемо:

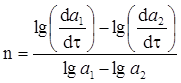(ХІ.6.8)

Початкові швидкості d a ₁/dt і d a ₂/dt визначають графічно з нахилу дотичної до початкової точки відповідної кінетичної кривої.

Поиск по сайту: