 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Образец выполнения индивидуальной домашней работы (ИДР)
1) Пользуясь свойствами определителей, доказать тождество 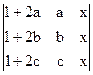 = 0
= 0
Решение. Пользуясь свойствами определителей 7), 4) и 6), получим
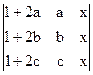 =
= 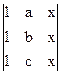 +
+  = x×
= x× 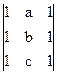 +2x×
+2x× 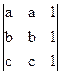 = 0 + 0 = 0.
= 0 + 0 = 0.
2) Дано: А = 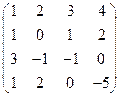 . Найти АТ; А×АТ и ½А½.
. Найти АТ; А×АТ и ½А½.
Решение.



















 1) АТ =
1) АТ = 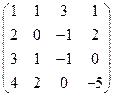 ; 2) А×АТ =
; 2) А×АТ = 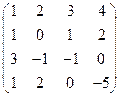 ×
× 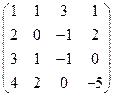 = =
= = 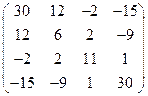 ; 3)
; 3)  ½А½=
½А½= 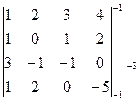 =
=  = =2×
= =2× 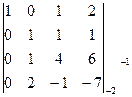 = 2×
= 2× 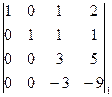 = 2×
= 2×  = 2×(-12) = -24.
= 2×(-12) = -24.
 |
3) Решить квадратную СЛАУ  .
.
а) матричным способом;
б) по формулам Крамера.
3а) Решение квадратной СЛАУ матричным способом
В этой СЛАУ А= 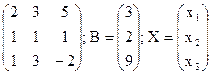 .
.
α) Методом элементарных преобразований найдем обратную матрицу А-1:




 (A|E) =
(A|E) =  ~
~  ~
~  ~
~




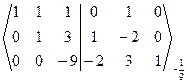 ~
~  -3 ~
-3 ~ 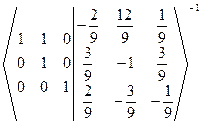 ~
~ 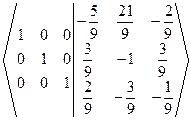 Þ А-1=
Þ А-1= 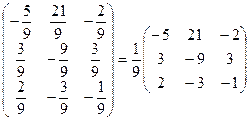
β) Проверка: А-1×А =  ×
×  =
= 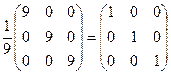 = Е
= Е
γ) По формуле (4.3) находим решение СЛАУ:
Х=А-1×В Þ 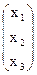 =
=  ×
× 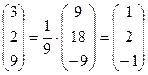 Þ х1 = 1; х2 = 2; х3 = -1
Þ х1 = 1; х2 = 2; х3 = -1
δ) Проверка. Подставляя значения х1 = 1, х2 = 2, х3 = -1 в исходную систему уравнений, получим
2×1+3×2+5×(-1)=3 Û 3º3
1+2+(-1)=2 Û 2º2
1+3×2-2×(-1)=9 Þ 9º9
Ответ: х1 = 1, х2 = 2, х3 = -1.
3б) Решение квадратной СЛАУ по формулам Крамера:
Главный определитель системы равен



 D=
D= 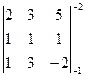 =
= 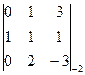 =
= 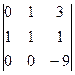 =
= 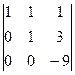 = 9 ¹ 0 Þ данная СЛАУ имеет единственное решение, определяемое формулами Крамера.
= 9 ¹ 0 Þ данная СЛАУ имеет единственное решение, определяемое формулами Крамера.









 D1 =
D1 = 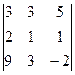 = -
= - 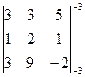 = -
= - 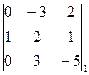 = -
= - 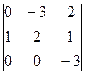 =
= 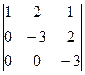 = 9 Þ
= 9 Þ
Þ х1 =  = 1.
= 1.









 D2 =
D2 = 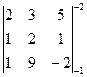 =
= 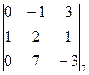 =
= 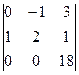 = -
= - 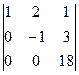 = 18 Þ х2 =
= 18 Þ х2 =  = 2.
= 2.








 D3 =
D3 = 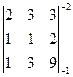 =
= 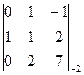 =
= 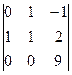 = -
= - 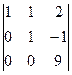 = -9 Þ х3 =
= -9 Þ х3 =  = -1.
= -1.
Ответ: х1 = 1, х2 = 2, х3 = -1.
4) Выполнить действия над матрицами: (А-1)2 + В×А, если А= 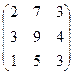 , В=
, В= 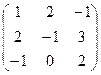 .
.
а) Методом элементарных преобразований над строками найдем обратную матрицу А-1.









 Решение: а) АЕ=(A|E)=
Решение: а) АЕ=(A|E)= 
 -1 ~
-1 ~ 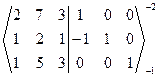 ~
~  ~
~ 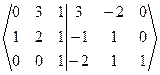 ~
~ 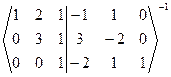 -1 ~
-1 ~


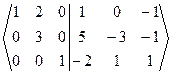 ~
~  ~
~ 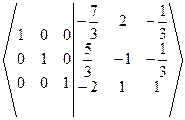 Þ ÞА-1=
Þ ÞА-1= 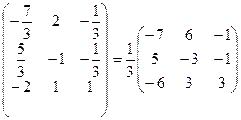 .
.
Проверка: А-1×А = 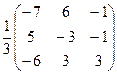 ×
× 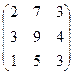 =
=  = Е;
= Е;
б) (А-1)2 = 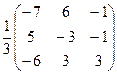 ×
× 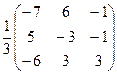 =
= 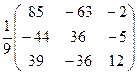 ;
;
в) В×А = 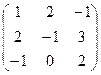 ×
× 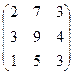 =
= 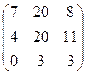 ; г) (А-1)2 + В×А =
; г) (А-1)2 + В×А = 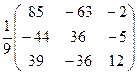 +
+ 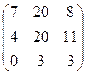 =
= 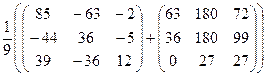 =
= 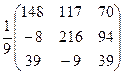 .
.
5) Найти значения l, для которых существует обратная матрица А-1, если А= 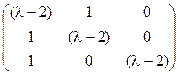 .
.
Решение. Обратная матрица А-1 существует, когда исходная матрица А является невырожденной, то есть ее определитель |А| ¹ 0. Найдем значения l, при которых определитель |А| = 0 и, исключив их, определим те значения l, при которых обратная матрица А-1 существует. Для этого разложим определитель данной матрицы по 3–му столбцу, так как он содержит только один ненулевой элемент (λ–2):


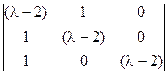 = (-1)6×(l-2)
= (-1)6×(l-2) 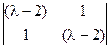 = (l-2)×((l-2)2 -1) = 0
= (l-2)×((l-2)2 -1) = 0
а) l = 2; б) (l-2)2 - –1 = 0 Þ l2 - 4l + 3 = 0 Þ 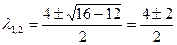 = 1; 3.
= 1; 3.
Таким образом, при l = 1; 2; 3 обратная матрица А-1 не существует. Значит, она существует во всех остальных случаях, когда l ¹ 1; 2; 3.
Ответ: Обратная матрица А-1 существует при l ¹ 1; 2; 3.
6) Найти ранг r(А) матрицы А, если А=  .
.
Решение. Элементарными преобразованиями приведем матрицу А к ступенчатому виду.








 А=
А= 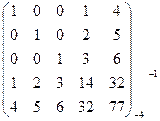 ~
~  ~
~ 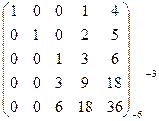 ~
~




 ~
~ 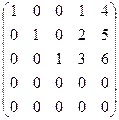 = В Þ r(A) = r(B) = 3. Ответ: r(A) = 3
= В Þ r(A) = r(B) = 3. Ответ: r(A) = 3
7(а) Исследовать СЛАУ на совместность и решить методом Гаусса.
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.
 |




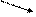


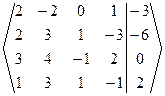 ~
~  ~
~ 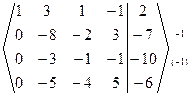 ~
~
































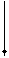



 ~
~ 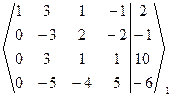 ~
~ 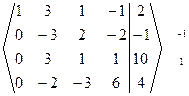
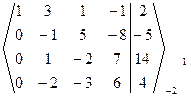 ~
~ 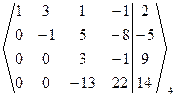 ~
~ 



 ~
~  ~
~ 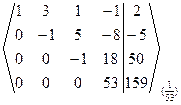 ~
~ 
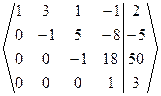 Þ Число неизвестных n = 4 = r(A) = =r(A|B), то есть ранги матрицы коэффициентов и расширенной матриц равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n = 4 = r(A) = =r(A|B), то есть ранги матрицы коэффициентов и расширенной матриц равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ 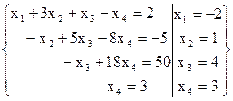
Проверка:
2×(-2)-2×1+3+3=0 Û 0º0
2×(-2)+3×1+4-3×3+6=0 Û 0º0
3×(-2)+4×1-4+2×3=0 Û 0º0
-2+3×1+4-3-2=0 Û 0º0
Ответ: х1 = -2, х2 = 1, х3 = 4, х4 = 3.
7(б) Исследовать СЛАУ на совместность и решить методом Гаусса.
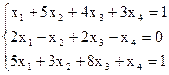
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.




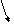

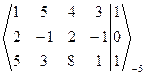 -2 ~
-2 ~  ~
~ 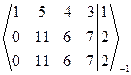 ~ ~
~ ~ 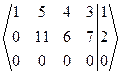 Þ Число неизвестных n = 4 > 2 = r(A) = r(A|B). По теореме Кронекера-Капелли данная система совместная и неопределенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n = 4 > 2 = r(A) = r(A|B). По теореме Кронекера-Капелли данная система совместная и неопределенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ 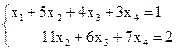
Поскольку число уравнений больше числа неизвестных, то нужно выбрать базисные неизвестные. В качестве базисных можно взять неизвестные х1, х2, так как коэффициенты при них образуют один из базисных миноров М2 =  = 11 ¹ 0.
= 11 ¹ 0.
Следовательно, остальные неизвестные х3, х4 – свободные. Зафиксируем их и, чтобы отличить от базисных неизвестных, переобозначим: пусть х3 = с3, х4 = с4. Перенесем их в правую часть соответствующих уравнений и выразим через них базисные неизвестные х1 и х2:
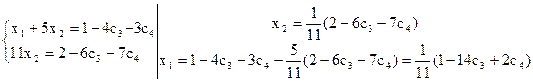
Ответ: х1 = 1/11(1-14с3+2с4); х2 = 1/11(2-6с3-7с4); х3 = с3; х4 = с4
8) Найти ненулевые решения однородной СЛАУ.

Решение. Запишем расширенную матрицу системы и элементарными преобразованиями над строками приведем ее к ступенчатому виду.






 -3 ~
-3 ~  ~
~  = B
= B
Число неизвестных n = 4 > 2 = r(A) = r(A|B), тогда, по теореме 1 (п.4.6), однородная СЛАУ помимо нулевого решения имеет и ненулевые решения. Найдем их. Полученной ступенчатой матрице В соответствует ступенчатая СЛАУ 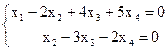
Чтобы решить ее, в качестве базисных неизвестных можно взять неизвестные х1 и х2, так как коэффициенты при них образуют один из базисных миноров М2 =  =1¹0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4, и перенесем в правую часть соответствующих уравнений.
=1¹0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4, и перенесем в правую часть соответствующих уравнений.

Ответ: х1 = 2с3-с4; х2 = 3с3+2с4; х3 = с3; х4 = с4, где с3, с4 - const.
Поиск по сайту: