Ранг матрицы. Если в прямоугольной матрице Аm´n выделить любые k строк и k столбцов (k min(m,n)), то элементы

Если в прямоугольной матрице А_m´n выделить любые k строк и k столбцов (k 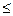min(m,n)), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу k–го порядка А_k. Определитель квадратной матрицы А_k называется минором k–го порядка исходной прямоугольной матрицы А_m´n, который обозначается символом М_k.

Опр. Минор k–го порядка М_k матрицы А называется базисным минором, если сам он не равен нулю, а все миноры более высоких порядков равны нулю.

NB. В матрице может быть несколько базисных миноров, но все они будут одного порядка.

NB. Строки и столбцы базисного минора называются базисными строками и столбцами.

Опр. Ранг матрицы есть порядок ее базисного минора. Ранг матрицы А обозначается символом r(A) или rang A.

NB.Только для нулевой матрицы О ее ранг r(O)=0.

Ранг матрицы не меняется:

1) при транспонировании матрицы;

2) если в матрице приписать или вычеркнуть нулевую строку (столбец);

3) при элементарных преобразованиях матрицы.

Опр. Матрица называется ступенчатой, если в каждой ее строке, начиная со второй, первый ненулевой элемент от начала строки расположен строго правее, чем первый ненулевой элемент предыдущей строки. Например,

A = или В =

NB. С помощью элементарных преобразований матрицу всегда можно привести к ступенчатому виду

Опр. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

NB. В ступенчатой матрице всегда можно выделить базисный минор треугольного вида с ненулевыми диагональными элементами, порядок которого равен числу ненулевых строк. Например, в матрице А можно выделить два таких базисных минора

М₄= 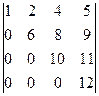и М^’₄= 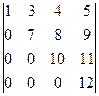, а в матрице В только один: М₄=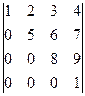

Пример. Найти ранг матрицы А=

Решение. Элементарными преобразованиями приведем матрицу А к ступенчатому виду.

А= ~ ~ ~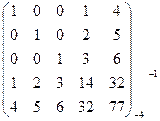

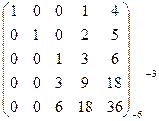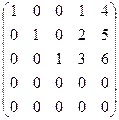~ = В Þ r(B) = 3. Так как А~В Þ r(А) = r(B) = 3.

Ответ: r(A) = 3

Поиск по сайту: