Обратная матрица. Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы

Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы А^т. Чтобы получить присоединенную матрицу , следует транспонировать матрицу А, а затем все ее элементы заменить их алгебраическими дополнениями, то есть

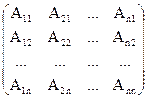= (3.1)

Опр. Квадратная матрица А называется вырожденной (особенной), если ее определитель |A|=0, и невырожденной, если ее определитель |A|¹0.

Опр. Квадратная матрица А^-1 называется обратной (инверсной) к квадратной матрице А, если выполняется условие

А^-1×А = А×А^-1= Е (3.2)

NB. Обратная матрица А^-1 возможна только для невырожденной матрицы А.

Теорема.

Для любой невырожденной квадратной матрицы А существует единственная обратная матрица А^-1, которая находится по формуле

А^-1 = 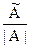(3.3)

Доказательство.

1) Из определения А^-1×А = А×А^-1 следует, что А и А^-1- это квадратные матрицы одного порядка.

Пусть матрица А – невырожденная, то есть |A|¹0. Тогда, по правилу умножения матриц, по теореме Лапласа и по свойству 9 определителей, получим

А× = × = =

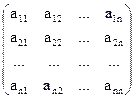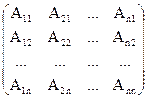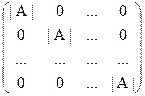= |A|× 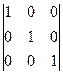= |A|×E

Следовательно, А× = |A|×E. Аналогично доказывается, что ×А = |A|×E.

Из А× = |A|×E Þ А^-1×А× 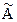= А^-1×|A|×E Þ Е× 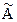=А^-1×|A| Þ 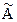=А^-1×|A| Þ А^-1 = .

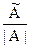2) Докажем единственность обратной матрицы. Предположим, что для матрицы А существует еще одна обратная матрица В. Тогда, согласно определению произведение А×В=Е. Обе части последнего равенства умножим слева на обратную матрицу А^-1 и получим: А^-1×А×В = А^-1×Е Þ Е×В = А^-1×Е Þ В = А^-1. Fin.

Свойства обратной матрицы:

1) |A^-1| = ;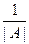

2) (A×B)^-1 = B^-1×A^-1;

3) (A^-1)^т = (А^т)^-1.

3.1.1. Вычисление обратной матрицы А^-1 с помощью присоединенной матрицы .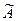

Для этого необходимо:

1) Вычислить определитель |A|. Если |A|=0, следовательно матрица А – вырожденная и для нее нет обратной матрицы А^-1. Если же |A|¹0, то следует выполнить следующие действия.

2) Вычислить алгебраические дополнения A_ij всех элементов a_ij матрицы А и построить матрицу А_А, в которой на местах элементов a_ij будут стоять их алгебраические дополнения A_ij:

А_А =

3) Транспонировать матрицу А_А, чтобы получить присоединенную матрицу :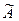

= = .

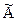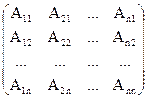4) Вычислить обратную матрицу А^-1 по формуле: А^-1 =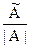

5) Выполнить проверку: А^-1×А = Е.

Пример. Дано: А= 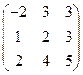, А^-1=?

Решение: 1) Вычислим определитель |A|. Для этого сначала «обнулим» первый столбец, а затем приведем определитель к треугольному виду.

|A| = 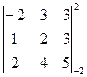= = 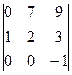– = 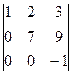-(–7) = 7 ¹ 0 Þ $ А^-1.

2) Найдем алгебраические дополнения A_ij всех элементов a_ij матрицы А:

А₁₁=(-1)² 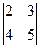= -2; А₁₂=(-1)³ 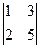= 1; А₁₃=(-1)⁴ 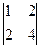= 0;

А₂₁=(-1)³ 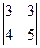= -3; А₂₂=(-1)⁴ 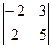= –16; А₂₃=(-1)⁵ 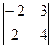= 14;

А₃₁=(-1)⁴ 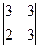= 3; А₃₂=(-1)⁵ = 9; А₃₃=(-1)⁶ = –7.

3) Составим матрицу А_А из алгебраических дополнений A_ij и транспонируем ее, чтобы получить присоединенную матрицу :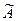

А_А= 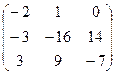Þ = = .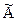

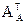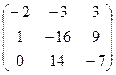4) Найдем обратную матрицу по формуле: А^-1 = = ∙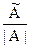

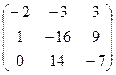
NB. В случае, когда |A| ¹ ±1, множитель 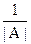лучше оставлять вне обратной матрицы А^-1 для удобства проверки.

5) Проверка: А^-1×А = ∙ ∙ 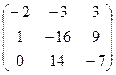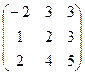= ∙ 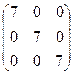= = 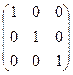Е.

Ответ: А^-1 = ∙ .

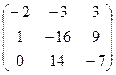3.1.2. Вычисление обратной матрицы А^-1

Поиск по сайту: