Понятие линейной зависимости и линейной независимости

В прямоугольной матрице A_m´n обозначим ее строки следующим образом:

(a₁₁ a₁₂ … a_1n) = а₁

(a₂₁ a₂₂ … a_2n) = а₂

_{……………………………..}

(a_m1 a_m2 … a_mn) = а_m

Опр. Строка а_m называется линейной комбинацией строк а₁, а₂, …, а_k (k<m), если ее можно представить в виде суммы попарных произведений этих строк на соответствующие числа l₁, l₂, …, l_k, то есть

а_m = l₁×а₁ + l₂×а₂ +…+ l_k×а_k = 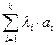(3.4)

NB. Вообще, линейной комбинацией величин а₁, а₂, …, а_k называется сумма попарных произведений этих величин на соответствующие числа l₁, l₂, …, l_k: 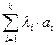, где l_i = const.

Опр. Величины а_i называются линейно независимыми, если их линейная комбинация равна нулю, то есть

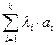= 0 (3.5)

только когда "l_i=0. В противном случае, если линейная комбинация (3.5) равна нулю хотя бы при одном l_i ¹0, то величины а_i называются линейно зависимыми.

Лемма.

Для того, чтобы величины а₁, а₂, …, а_k были линейно зависимыми, необходимо и достаточно, чтобы хотя бы одна из них была линейной комбинацией остальных.

Доказательство.

1) Необходимость. Пусть величины а₁, а₂, …, а_k линейно зависимы. Это означает, что равенство (3.5) выполняется, например, при l₁¹0. Разделив равенство (3.5) на l₁и выразив а₁ через остальные величины, получим

а₁= , (3.6)

где .

Равенство (3.6) означает, что величина а₁ является линейной комбинацией остальных величин: а₂, …, а_k.

2) Достаточность. Пусть, например, величина а₁ является линейной комбинацией величин а₂, …, а_k, то есть имеет место равенство (3.6). Перенесем а₁ в правую часть и получим:

(-1)а₁ + = 0

Так как коэффициент при а₁ отличен от нуля, а линейная комбинация величин а₁, а₂, …, а_k равна нулю, то величины а₁, а₂, …, а_k линейно зависимы. Fin.

Теорема (о базисном миноре).

1) Базисные строки (столбцы) матрицы – линейно независимы.

2) Любая небазисная строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).

Доказательство.

1) Допустим, что базисные строки (столбцы) матрицы являются линейно зависимыми. Тогда, согласно лемме, одна из них является линейной комбинацией остальных и, исходя из свойств определителя, базисный минор такой матрицы будет равен нулю, что противоречит определению базисного минора. Значит, базисные строки (столбцы) матрицы являются линейно независимыми.

2) Перестановкой строк и столбцов, то есть элементарными преобразованиями, добьемся того, чтобы базисный минор располагался в первых k строках и k столбцах матрицы A_m´n. Тогда любой минор (k + 1)-го порядка и выше будет равен нулю, то есть строки (столбцы) матрицы, начиная с номера (k + 1) будут линейно зависимыми. Поэтому каждая из этих строк (столбцов) будет представлять собой линейную комбинацию каких-то других (остальных) строк (столбцов). Следовательно, элементарными преобразованиями их можно обнулить. В результате получится матрица, у которой, начиная с (k + 1)-го номера, все строки и столбцы будут нулевыми, а ненулевыми останутся только первые k базисных строк и столбцов, поскольку они линейно независимы. Тогда в обратном порядке мы можем восстановить первоначальный вид матрицы, оперируя только ее базисными строками и столбцами (так как только они остались ненулевыми). Следовательно, любая небазисная строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов). Fin.

Теорема (о ранге матрицы).

Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) этой матрицы.

Доказательство. Пусть r(A)=k, тогда k строк матрицы А, составляющие ее базисный минор, являются линейно независимыми. По теореме о базисном миноре любая другая строка вне базисного минора является линейной комбинацией базисных строк. Поэтому число k является максимальным числом линейно независимых строк. Fin.

Следствие. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов в этой матрице.

Теорема (о линейной зависимости строк (столбцов) определителя).

Для того чтобы определитель D равнялся нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимыми.

Доказательство.

1) Необходимость. Пусть определитель D=0, тогда порядок его базисного минора меньше порядка определителя. Следовательно, хотя бы одна строка (столбец) определителя является небазисной. Тогда по теореме о базисном миноре, эта строка (столбец) является линейной комбинацией базисных строк (столбцов), и значит все строки (столбцы) определителя будут линейно зависимыми.

2) Достаточность. Если строки (столбцы) определителя D являются линейно зависимыми, то по лемме, хотя бы одна из них является линейной комбинацией базисных строк (столбцов). Следовательно, определитель D=0. Fin.

Пример 1. Являются ли указанные векторы линейно зависимыми?

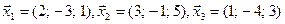
Решение. Составим определитель D из координат векторов. Если D=0, то приведенные векторы линейно зависимы, а если D¹0, то нет.

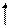
D = ^-3 = = -5 ^-11 = -5 = 5 =

= 5×7 = 35 ¹ 0 Þ указанные векторы линейно независимы.

Поиск по сайту: