Матричный способ решения квадратной СЛАУ

Для квадратной СЛАУ определитель матрицы коэффициентов (определитель матрицы А) называется главным определителем этой СЛАУ. Он обозначается одним из символов

D, |A|,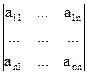

Если квадратная матрица А невырожденная, то ее определитель D¹0 и, следовательно, $А^-1.

Если обе части матричного уравнения (4.2) умножить слева на обратную матрицу А^-1, то получится решение квадратной СЛАУ в матричной форме:

А^-1×А×Х=А^-1×В Þ Е×Х= А^-1×В Þ

Þ Х= А^-1×В (4.4)

Таким образом, чтобы найти решение квадратной СЛАУ, надо матрицу А^-1, обратную матрице коэффициентов СЛАУ, умножить слева на матрицу-столбец свободных членов В.

Пример. Решить систему уравнений

Решение.

Это квадратная СЛАУ, где А= .

1) Находим обратную матрицу А^-1 методом элементарных преобразований над строками:

(A|E) = ~ ~ ~

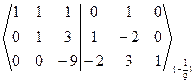~ ~ ^-3 ~ ~ 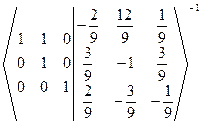~ 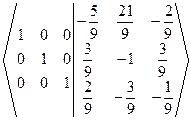Þ А^-1=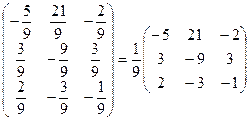

2) Проверка: А^-1×А = × = = 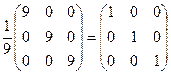Е

3) Решение СЛАУ находится по формуле (4.4):

Х = А^-1×В Þ 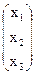= × 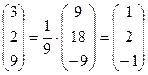Þ х₁ = 1, х₂ = 2, х₃ = -1.

4) Проверка. Подставляя значения х₁ = 1, х₂ = 2, х₃ = -1 в исходную систему уравнений, получим

2×1+3×2+5×(-1)=3 Û 3º3

1+2+(-1)=2 Û 2º2

1+3×2-2×(-1)=9 Þ 9º9.

Ответ: х₁ = 1, х₂ = 2, х₃ = -1

Поиск по сайту: