Правила вычисления определителей

Опр. Определитель 1-го порядка – это определитель квадратной матрицы 1-го порядка А₁, который равен значению элемента а₁₁, так как матрица А₁ состоит из одного этого элемента, который одновременно является ее числовой характеристикой: D=|A₁|= a₁₁.

Опр. Определитель 2-го порядка – это определитель квадратной матрицы 2-го порядка А₂, который вычисляется по формуле

D = |A₂| = 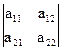= a₁₁×a₂₂ - а₁₂×а₂₁, (2.1)

то есть он равен разности произведений элементов главной и побочной диагоналей (рис.2.1).

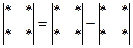
Рисунок 2.1

Пример. 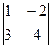=1×4 - (-2)×3 = 10

Опр. Определитель 3-го порядка – это определитель квадратной матрицы 3-го порядка А₃, который вычисляется по формуле

D = |A₃| = =

= а₁₁×а₂₂×а₃₃ + а₁₂×а₂₃×а₃₁ + а₁₃×а₂₁×а₃₂ - а₁₃×а₂₂×а₃₁ - а₁₂×а₂₁×а₃₃ - а₁₁×а₂₃×а₃₂ (2.2)

Для запоминания формулы (2.2) используют правило треугольников, которое символически изображено на рисунке 2.2.

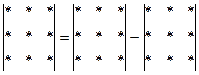
Рисунок 2.2

Со знаком (+) берутся произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих в вершинах треугольников, основания которых параллельны главной диагонали. Со знаком (-) берутся произведения элементов, стоящих на побочной диагонали, и произведения элементов, стоящих в вершинах треугольников, основания которых параллельны побочной диагонали.

Пример. D= 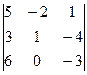= 5×1×(-3) + (-2)×(-4)×6 + 3×0×1 - 1×1×6 - (-2)×3×(-3) - (-4)×0×5 = 9

Опр. Минор M_ij элемента a_ij - это определитель, который получается из исходного определителя вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент a_ij. Например,

if D= Þ M₁₁ = , то есть М₁₁ = ; М₁₂ = ,…,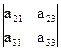

М₃₃ =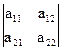

Опр. Алгебраическое дополнение A_ij элемента a_ij - это минор M_ij, взятый со знаком (-1)^i+j, то есть A_ij = (-1)^i+j×M_ij. Например,

if D= 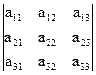Þ А₁₁=(-1)²× М₁₁ = ; А₁₂=(-1)³× М₁₂ = - 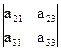,…, А₃₃=(-1)⁶× М₃₃ = .

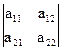Теорема Лапласа (точнее, частный случай теоремы Лапласа).

Всякий определитель равен сумме попарных произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения, то есть

D = |A_n| = 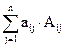= , (2.3)

где 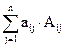есть разложение определителя по i-ой строке, а есть разложение определителя по j-му столбцу.

Доказательство.

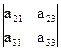Убедимся в справедливости теоремы Лапласа на примере разложения определителя 3-го порядка, например, по 1-й строке. По теореме это разложение будет иметь вид: D= = а₁₁А₁₁ + а₁₂А₁₂ + а₁₃А₁₃ = {с учетом определения A_ij получим}= =а₁₁(-1)²М₁₁ + а₁₂(-1)³М₁₂ + а₁₃(-1)⁴М₁₃ = а₁₁ - а₁₂ + а₁₃ = а₁₁(а₂₂×а₃₃ - а₂₃×а₃₂) - а₁₂(а₂₁×а₃₃ - а₂₃×а₃₁) + а₁₃(а₂₁×а₃₂ - а₂₂×а₃₁) = =а₁₁×а₂₂×а₃₃ + а₁₂×а₂₃×а₃₁ + а₁₃×а₂₁×а₃₂ - а₁₃×а₂₂×а₃₁ - а₁₂×а₂₁×а₃₃ - а₁₁×а₂₃×а₃₂ = {по правилу треугольников} = = D. Аналогичный результат получается при разложении определителя по любой строке (столбцу). Fin.

Следствие. Если в i–й строке (j-м столбце) определителя D есть только один ненулевой элемент а_ij ¹ 0, то результатом разложения определителя по этой строке (столбцу) будет выражение D = а_ij×А_ij.

Поиск по сайту: