Исследование СЛАУ. Теорема Кронекера-Капелли

Пусть дана прямоугольная СЛАУ (4.1) из m уравнений с n неизвестными. Этой СЛАУ соответствует краткая запись в виде расширенной матрицы, которая состоит из матрицы коэффициентов А и матрицы–столбца свободных членов В, разделенных вертикальной разделительной чертой, то есть в виде (A|B). В ней каждая строка соответствует алгебраическому уравнению исходной СЛАУ.

(A|B)= (4.7)

Теорема Кронекера-Капелли (критерий совместности СЛАУ).

СЛАУ совместна тогда и только тогда, когда ранг матрицы коэффициентов равен рангу расширенной матрицы r(A) = r(A|B).

Доказательство.

1) Необходимость. Пусть СЛАУ (4.1) совместна. Запишем ее в виде суммы матриц-столбцов (4.3):

+ +…+ =

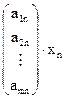Это означает, что если существует решение x₁= C₁, …, x_n = C_n, то столбец свободных членов является линейной комбинацией столбцов матрицы коэффициентов СЛАУ. Следовательно, ранг матрицы коэффициентов равен рангу расширенной матрицы: r(A) = r(A|B).

2) Достаточность. Пусть r(A) = r(A|B). Это означает, что для данной СЛАУ любой базисный минор матрицы коэффициентов А остается базисным и для расширенной матрицы A|B. Тогда по теореме о базисном миноре, столбец свободных членов расширенной матрицы A|B можно представить в виде линейной комбинации базисных столбцов матрицы А, то есть существуют числа l_i (i= ), не все равные нулю, при которых выполняется равенство

+ +…+ = Þ λ₁ = x₁; …; λ_n = x_n

Следовательно, значения коэффициентов l_i этой линейной комбинации и есть решение СЛАУ (4.1), то есть СЛАУ (4.1) является совместной при r(A) = r(A|B). Fin.

Следствие 1. Если ранги матрицы коэффициентов и расширенной матрицы СЛАУ равны числу неизвестных (r(A) = r(A|B) = n), то такая СЛАУ имеет единственное решение (то есть СЛАУ является совместной и определенной).

Следствие 2. Если ранги матрицы коэффициентов и расширенной матрицы СЛАУ равны друг другу и меньше числа неизвестных (r(A) = r(A|B) < n), то такая СЛАУ имеет бесконечное множество решений (то есть СЛАУ является совместной и неопределенной).

Следствие 3. Если ранг матрицы коэффициентов меньше ранга расширенной матрицы r(A)< r(A|B), то такая СЛАУ решений не имеет (то есть СЛАУ является несовместной).

Пример. Исследовать СЛАУ на совместность

Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду

~ ~ ~ ~

Þ r(A) = 3; r(A|B) = 4 Þ r(A) < r(A|B) Þ СЛАУ не совместна.

Действительно, последней строке ступенчатой расширенной матрицы СЛАУ соответствует уравнение, которое не имеет решений ни при каких значениях неизвестных х₁, х₂, х₃: 0×х₁ + 0×х₂ + 0×х₃ = -1.

Поиск по сайту: