Mathematical models of growth of number of a population

All processes in communities of alive objects occur in time and in space. In some cases it is possible to consider, that in all parts of the considered volume processes are synchronous. In this case the elementary dot models are described by system of the differential equations.

where х - number of i -th population (the kinetic equations).

Sizes - nonlinear functions.

As a rule, they consist of several composed. Positive members describe profit of a component, negative - its loss.

Let's consider three mathematical models, allowing to define dependence of change of number of a population on time for various conditions of functioning of system.

1. Model of natural growth of number of a population (model Maltys).

The model under the described scheme is created.

Real system: there is some population of one kind (microorganisms, hares, etc.) in which there are vital processes in all of them variety.

Statement of a problem. To find laws of change of number of a population on time.

The basic assumptions:

1. There are only processes of duplication and natural destruction, speeds of processes of duplication and natural destruction are proportional to number of individuals at present to time.

2. It is not considered biochemical, physiological processes.

3. There is no struggle between individuals for a place of dwelling, for food (infinitely big space and quantity peep).

4 It Is considered only one population, there are no predators.

Let's enter sizes:

x - number of a population during the moment t,

R -Speed of duplication,

- factor of duplication,

S-speed of natural destruction,

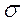- factor of natural destruction

- speed of change of number of a population

T hen .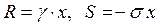

Let's write the differential equation of balance. Change of number of individuals in unit of time is defined by quantity born for this time and died:

or ,

T he entry condition: at t=0 number of individuals

Let's solve the equation: ,

fro m here

The analysis of the decision.

1. <0 (at , speed of destruction is more than speed of duplication. Number of individuals in due course will fall up to zero (fig. 2.a);

Change of number of a population for the lack of a competition between individuals at <0 (а) and at >0 (б) (fig. 2. б).

Fig. 2.

2. >0 (at , speed of duplication is more than speed of destruction. Number of individuals beyond all bounds grows in due course. (fig. 2.б);

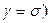3. (at , speed of destruction is equal to speed of duplication. Number of individuals does not change, remaining at an initial level.

At >0 The model is adequate to a reality up to the certain values of time. According to the given model considering reduction of number of individuals only due to natural destruction, their number should increase infinitely in due course (fig. 2.б), that will not corresponding with reality. At a plenty of individuals probably reduction of their number due to other mechanisms, for example, due to struggle for a place of dwelling, for food.

For approach of the given model a reality it is necessary to remove assumptions. Let there is a struggle between individuals, for a place of dwelling, presence of predators therefore is added an additional source of destruction.

The equations of balance between number of the born and perishing individuals passes in complex system of the differential equations.

Decisions of system of the differential equations

If we shall solve this system of the equations, we shall receive, that number of populations х and at test harmonious fluctuations concerning stationary values with identical frequency y, but displaced on a phase. Periodicity of change of number of predators and victims was observed and on experience. On fig. 3 skilled data by quantity of number of the extracted skins of hares and lynces in Canada with 1845 on 1935 are cited is visible, that in a real case of dependence more complex, than it follows from model. The sine wave decision is possible only at small deviations U and V concerning stationary values. At greater deviations the law will not be harmonious.

Dependence y from х can be presented in the form of a phase portrait. For periodic dependences the portrait looks like an ellipse (fig. 4.) which center corresponds to stationary values.

Fig. 4.

Поиск по сайту: