The equation of Hill. Power of single reduction

Dependence of speed of shortening on loading Р is the major at studying work of a muscle as allows to reveal laws of muscular reduction and its power. Hill studied it in detail at different modes of reductions and presented on fig. 8.

He has offered the equation describing this curve

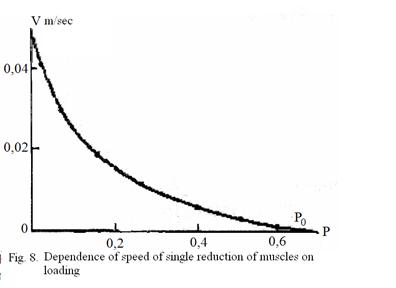
This expression refers to as the equation of Hill and is the basic equation of mechanics of muscular reduction.

Р₀ - the maximal isometric pressure developed by a muscle, or the maximal cargo which is held with a muscle without lengthening; b - a constant which has dimension of speed, and - a constant, dimensional forces.

From equation we get, that speed becomes maximal at Р = 0,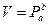

At Р = Р₀ it is received V = 0, that is shortening does not occur. Work A, made by a muscle at single shortening on size is equal to А= Р .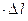

Dependence of capacity on developed force Р

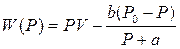
Capacity is equal to zero at Р =Р₀ and Р = 0 and reaches the maximal value at optimum size of loading

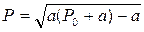
The overall performance of a muscle at reduction can be certain as the attitude of the perfect work to the spent energy : .

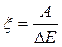Development of the greatest capacity and efficiency of reduction is reached at efforts

0,3 - 0,4 from maximal isometric loadings Р₀, for the given muscle. It is used, for example, by sportsmen-bicycle racers: at transition from plain on a mountain site loading on muscles increases also the sportsman switches speed to the lowest transfer, reducing Р, approaching it to Р_max. Practical efficiency can reach values of 40-60 % for different types of muscles. The highest efficiency is observed at muscles of the turtle, reaching 73 - 80 %.

Поиск по сайту: