АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обчислення суми членів числової послідовності

Читайте также:
  1. Блок обчислення математичних функцій Math Function
  2. Блок обчислення похідної Derivative
  3. Блок обчислення суми Sum
  4. Вивчення послідовності вивірення кулеметів та прицілу по контрольній мішені.
  5. Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання
  6. Г) обчислення й аналіз результатів.
  7. Елементи літературно-критичних суджень у творчості членів «Руської трійці» після навчання в семінарії
  8. Індивідуальні завдання з теорії многочленів
  9. Межа послідовності комплексних чисел
  10. Методика навчання учнів розв’язувати задачі на обчислення периметра та площі геометричних фігур.
  11. Методика обчислення теоретичних частот нормального розподілу
  12. Обов’язки членів дружини
Числова послідовність – це однозначне зображення множини натуральних чисел на множині дійсних чмсел. Це функція натурального аргумента, що являє собою загальний член послідовності. Загальний член послідовності (ЗЧП) – це формула, за якою за номером члена послідовності можна знаходити сам член послідовності.

 

З математики нам відомі арифметична і геометрична прогресії.

Арифметична прогресія – це послідовність чисел, кожне з яких, починаючи з другого, обчислюється із попереднього додаванням до нього постійного (для всіх членів послідовності) числа, названого різницею прогресії. Різницю прогресії позначають буквою d.

 

Формули будь-якого члена арифметичної прогресії і суми перших її n членів:

an=a1+nd, (1)

 

Геометрична прогресія – це послідовність чисел, кожне з яких, починаючи з другого, дорівнює попередньому, помноженому на деяке постійне для даної послідовності число, що називають знаменником прогресії і позначають буквою q.

Формули будь-якого члена геометричної прогресії і суми перших n членів:

(2)

Формули (1) і (2), звичайно ж, можна використовувати у роботі з цими прогресіями.

 

Ми розглянемо інший підхід до обчислення суми членів числової послідовності.

Наведемо кілька прийомів знаходження загального члена послідовності:

1.Послідовність є арифметичною прогресією. У цьому випадку знаходимо різницю прогресії, множимо її на номер поточного члена послідовності (і) і додаємо або віднімаємо таке число, щоб одержати перший член послідовності. Наприклад:

1, 5, 9, 13, … - загальний член дорівнює:

2, 8, 14, 20, … - загальний член дорівнює: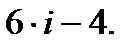

2.Послідовність є геометричною прогресією. У цьому випадку знаходимо знаменник прогресії (q) і записуємо формулу у вигляді: qi. Наприклад: 2, 4, 8, 16, … - загальний член дорівнює: 2і.

3.Послідовність не є арифметичною або геометричною прогресією, але різниці між сусідніми членами утворюють геометричну прогресію. У цьому випадку записуємо формулу загального члена для послідовності, отриманої з різниць, а потім для одержання остаточної формули додаємо або віднімаємо таке число, щоб одержати перший член вихідної послідовності. Наприклад: 1, 3, 7, 15 … Послідовність, складена з різниць сусідніх членів, має вигляд: 2, 4, 8, 16, … Її загальний член 2і, а формула загального члена вихідної послідовності: 2і – 1.

4.Елементи послідовності, що знаходяться на непарних місцях, утворюють арифметичну прогресію, аналогічно елементи, що містяться на парних місцях, теж утворюють арифметичну прогресію. Наприклад: 4+1+5+2+6+3+7+4+8+… Формулу загального члена послідовності будемо шукати в такий спосіб:

Спочатку знайдемо формулу загального члена для елементів, що стоять на непарних місцях у послідовності (для непарних індексів): 4+5+6+7+8+…

Для цього складемо систему рівнянь:

Множники 1 і 3 – порядкові номери членів послідовності, а х та у – деякі числа. Розв’язуючи систему, знаходимо, що а

Отже, формула загального члена для елементів, що містяться на непарних місцях у послідовності, має вигляд:

Міркуючи аналогічно, знайдемо формулу загального члена для елементів послідовності, що знаходяться на парних місцях у послідовності: 1+2+3+4+5+…

Знаходимо: Формула загального члена -

Отримані формули повинні працювати по черзі. Цього легко досягти за допомогою виразу:

Перетворивши його, одержимо остаточну формулу загального члена числової послідовності:

Алгоритми для обчислення суми членів числової послідовності мають той самий вигляд:

1.Уведення кількості членів послідовності.

2.Обнуління комірки для підсумування або занесення в неї члена послідовності, що не може бути отриманий із загального члена.

3.Організація циклу, всередині якого буде команда присвоювання, що має структуру:

s:=s+зчп,

де S – комірка для підсумовування.

4.Виведення результату.

 

Наведемо кілька прикладів з обчислення суми членів числової послідовності.

Приклад 1. Обчислити суму N членів послідовності:

Алгоритм має вигляд:

АЛГ Сума членів послідовності (ціл N, дійсн S)

АРГ N

РЕЗ S

ПОЧ ціл і

і:=1; S:=0

поки i<=N

пц

S:=S+i/(i+1)

і:=i+1

кц

ДРУКУВАТИ S

КІН

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)