Приклади алгоритмів

Приклад 1. Побудувати за допомогою циркуля і лінійки бісектрису кута.

Алгоритм побудови має вигляд:

1.Встановити ніжку циркуля у вершину кута А.

2.Провести коло довільного радіуса.

3.Позначити точки перетину В і С із сторонами кута.

4.Провести коло з точки В тим самим радіусом.

5.Провести коло з точки С тим самим радіусом.

6.Позначити точку D їх перетину (що не збігається з вершиною кута).

7.Провести пряму AD. Бісектрису кута побудовано.

Приклад 2. Розв’язати лінійне рівняння ax+b=0.

Пригадаємо, як ми розв’язували такі рівняння. Якщо 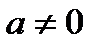, то маємо єдиний розв’язок якщо 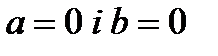, то будь-які значення х є розв’язком даного рівняння; якщо 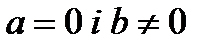тоді таке рівняння не має розв’язку.

Запишемо алгоритм у вигляді команд:

1.Перевірити, чи a дорівнює нулю. Якщо так перейти до пункту 5, якщо ні – продовжити обчислення.

2.Розділити b на а.

3.Видати результат: «х=».

4.Закінчити роботу.

5.Перевірити, чи дорівнює b нулю. Якщо так, перейти до пункту 8, якщо ні – продовжити обчислення.

6.Видати результат: «х – будь-яке число».

7.Закінчити роботу.

8.Видати результат: «Рівняння не має розв’язку».

9.Закінчити роботу.

Залежно від значень а і b в алгоритмі будуть виконуватися або команди 1, 2, 3, 4 (якщо 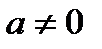), або 1, 5, 6, 7 (якщо 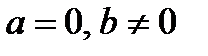), або 1, 5, 8, 9 (якщо ).

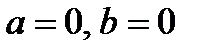У наведеному прикладі в алгоритмі передбачено випадок, коли а=0. Якщо не досліджувати чи а і b дорівнюють нулю, то алгоритм буде значно коротшим:

1.Розділити b на a.

2.Видати результат: «х=».

3.Закінчити роботу.

Але в тому випадку, коли виявиться, що а=0, виконавець перерве роботу, тому що виконувати ділення на нуль неможливе, і не буде відомо, який з двох випадків мав місце: «рівняння не має розв’язку», або «має нескінченну множину розв’язків».

У всіх випадках, коли, дотримуючись алгоритму, виконавець не може виконати певні дії (поділити на нуль, обчислити корінь з від’ємного числа, обчислити логарифм від’ємного числа тощо), робота припиняється. Такі ситуації, як правило, є наслідком помилки в алгоритмі, яку слід знайти і виправити. У цьому випадку алгоритм не має властивості масовості, тоді як у першому випадку ця властивість виконується.

Отже, під час складання алгоритмів необхідно пам’ятати про властивості алгоритмів.

Приклад 3. Виконати операцію ділення двох натуральних чисел (а:b) шляхом віднімання. Результат ділення подати у вигляді цілої частини і залишку.

Запишемо алгоритм обчислення у вигляді команд:

1.Комірку для зберігання цілої частини частки «обнулити» (k:=0).

2.Порівняти числа а і b (a=b) і якщо умова істинна, то перейти до пункту 3, інакше перейти до пункту 6.

3.Лічильник цілої частини збільшити на одиницю (k:=k+1).

4.Від а відняти b і результат помістити в комірку а (a:=a – b).

5.Перейти до пункту 2.

6.Видати результат: «у комірці k значення цілої частини числа, а в комірці а – залишок від ділення».

Отже, ми розглянули приклади лінійного, розгалуженого та циклічного алгоритмів. Обмежимося цими прикладами, а ви спробуйте самі згадати відомі вам алгоритми.

Поиск по сайту: