АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обчислення суми функціональної послідовності

Читайте также:
  1. Блок обчислення математичних функцій Math Function
  2. Блок обчислення похідної Derivative
  3. Блок обчислення суми Sum
  4. Вивчення послідовності вивірення кулеметів та прицілу по контрольній мішені.
  5. Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання
  6. Г) обчислення й аналіз результатів.
  7. Межа послідовності комплексних чисел
  8. Методика навчання учнів розв’язувати задачі на обчислення периметра та площі геометричних фігур.
  9. Методика обчислення теоретичних частот нормального розподілу
  10. Обчислення границь символічних виразів
  11. Обчислення добутку членів послідовності
  12. Обчислення економічних збитків
Функціональна послідовність – це відображення множини натуральних чисел N у множину дійсних функцій однієї змінної х, дійсної на деякому інтервалі.

 

З курсу вищої математики відомо, що всі елементарні функції можуть бути подані функціональною нескінченною послідовністю або, як кажуть, розкладені у функціональний ряд.

Наведемо кілька прикладів розкладань функцій у ряд:

1)

 

2)

 

3)

 

4)

При всіх значеннях х ряди (1 – 3) сходяться і дають відповідну функцію. Ряд (4) сходиться в інтервалі (- 1, 1). Цими рядами користуються для обчислення значень функцій. Відомі вам таблиці Брадіса створювалися саме в такий спосіб.

Обчислимо, наприклад, sin100 з точністю до 10-5. Переведемо 100 в радіани за формулою: одержимо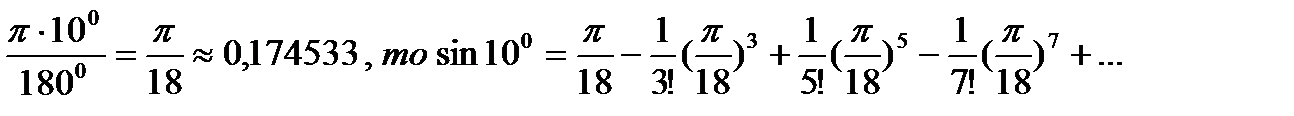

Обмежимося першими двома членами: Одержимо:

Знаходження суми членів функціональною послідовністю або рядом простіше виконувати, використовуючи рекурентну формулу. Це дає можливість уникнути обчислення факторіала при одержанні чергового члена послідовності.

Розглянемо приклад обчислення значення cosx, використовуючи її розкладання в ряд за степенями х для N членів та із заданим степенем точності

Загальний член послідовності має вигляд рекурентної формули: де k – коефіцієнт, що обчислюється за формулою: Він знаходиться шляхом ділення поточного члена послідовності на попередній, причому вони повинні бути записані у загальному вигляді. Поточний член має вигляд: а попередній – 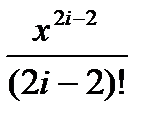, оскільки ми працюємо з парними числами, то:

Для виконання скорочень використовували рівність: (2і)!=(2і – 2)!(2і – 1)2і.

 

Алгоритм обчислення значення функції cosx має вигляд:

Обчислення заданої кількості доданків: Обчислення до досягнення заданої точності:
АЛГ Cosx (цілий N, дійсн X, S) АРГ X, N РЕЗ S ПОЧ дійсн K, U; ціл і S:=0; U:=1; i:=1 поки i<=n пц S:=S+U U:=U*K і:=i+1 кц   ДРУКУВАТИ S КІН АЛГ Cosx (дійсн X, E, S) АРГ X, E РЕЗ S ПОЧ дійсн K, U; ціл і S:=0; U:=1; i:=1 поки пц S:=S+U U:=U*K і:=i+1 кц   ДРУКУВАТИ S КІН

 

 

Алгоритм мовою Паскаль:  
Program Cosx1; var i, N: word; x, s, u, k: real; begin write(‘ Введіть кількість доданків ‘); readln(n); s:=0; u:=1; for i:=1 to N do begin s:=s+u; k:= - x*x/((2*i – 1)*2*i); u:=u*k; end; writeln(‘s=’, s:8:2); end. Program Cosx2; var i: word; x, s, Eps, k, u: real; begin write(‘ Введіть точність результату ‘); readln(Eps); s:=0; u:=1; i:=1; while abs(u)>Eps do begin s:=s+u; k:= - x*x/((2*I – 1)*2*i); u:=u*k; i:=i+1; end; writeln(‘s=’, s:8:2); end.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)