 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Транспортна задача
Виділення транспортної задачі в окремий розділ обумовлено тим, що ця задача має специфічну економіко-математичну модель і може розв’язуватися не універсальним симплекс-методом, а за допомогою так званного розподільного методу і його різноманітних модифікацій.
Найпростішими транспортними задачами є задачі перевезення деякого однорідного вантажу від постачальників до споживачів при забезпеченні мінімальних витрат на перевезення.
Початкові умови таких задач записують у вигляді таблиці. Наприклад, для m постачальників і n споживачів така таблиця має наступний вигляд:
Таблиця 1.7.1
| Споживачі та їх потреби | |||||||
| Постачальники | B1 | B2 | … | Bj | … | Bn | |
| A1 | С11 | С12 | ... | С1j | ... | С1n | |
| A2 | С21 | С22 | ... | С2j | ... | С2n | |
| … | ... | ... | ... | ... | ... | ... | |
| Ai | Сi1 | Сi2 | ... | Сij | ... | Сin | |
| … | ... | ... | ... | ... | ... | ... | |
| Am | Сm1 | Сm2 | ... | Сmj | ... | Сmn |
В таблиці представлено інформацію про потужність постачальників Ai (i = 1,m), потребу споживачів Bj (j = 1,n), а також витрати на перевезення від i - го постачальника j -му споживачу Cij.
Позначимо через xij кількость постачання вантажу від i - го постачальника j -му споживачу. Математично транспортна задача зводиться до знаходження мінімуму цільової функції, яка задає сумарні витрати на перевезення усього вантажу:
F = c11x11 + c12x12 + … + cijxij + … + cmnxmn ® min (1.7.1)
При обмеженнях
X11 + x12 + … + x1n = A1,
X21 + x22 + … + x2n = A2,
.....................
xm1 + xm2 + … + xmn = Am, (1.7.2)
x11 + x21 + … + xm1 = B1,
x12 + x22 + … + xm2 = B2,
.....................
x1n + x2n + … + xmn = Bn.
Якщо в транспортній задачі сумарна потужності всіх постачальників равна сумарній потребі всіх споживачів, то відповідну математичну модель задачі називають закритою, або моделлю з правільним балансом. В іншому випадку – відкритою, або не сбалансованою.
Економіко-математична модель транспортної задачі має наступні особливості і відрізняється від звичайних задач лінейного програмування в загальному вигляді, а саме:
- система обмежень (1.7.2) має вигляд рівнянь, тому відпадає необхідність вводити додаткові змінні;
- матриця коефіцієнтів при змінних в системі (1.7.2) складається тільки з одиниць та нулів;
- система (1.7.2) є системою n + m рівнянь з nm невідомими.
Така специфічність економіко-математичної моделі транспортної задачі привела до появи особливих методів її розв’язування.
Рішення транспортної задачі починається з пошуку початкового розподілу постачань. Найбільш розповсюджуваними методами є метод “північно-західного кута” і метод “найменших витрат”.
Пошук початкового розподілу постачань за методом “північно-західного кута”. До початку розподілу перевіряємо баланс між сумарною потужністю всіх виробників та сумарною потребою всіх споживачів. Якщо задача сбалансована починаємо виконувати розподіл у наступної послідовності.
“Північно-західний кут” це сама верхня, ліва клітинка. Визначаємо потужність першого виробника. Якщо виробник має потужність більшу, ніж потреба споживача, то в клітинку заносимо кількість вантажу, яка равна повної потреби споживача. Для розподілу залишку переходимо до наступної правої клітинки. Для цієї клітинки виконуємо аналогічний розподіл. Якщо на якому-небудь кроці не вистачє потужності виробника, в клітинку занаситься все, що є у нього і розподіл переносится до наступного виробника та розглядається клітинка, яка зв’язує цього виробника зі споживачем. Розподіл за наступною методикою виконується до останього постачальника і останього споживача. Так як задача збалансована, то розподіл буде виконано повністю.
Для перевірки вартості постачань за таким розподілом необхідно підрахувати суму добутків кількості постачань і їх вартості для всіх заповнених клітинок. Метод “північно-західного кута” найбільш дозволяє просто виконати розподіл, але він не враховує вартість постачань безпосередньо під час розподілу. Тому має низьку ефективність.
Приклад 1. Скласти оптимальний план перевезень однорідного вантажу від виробників до споживачів, якщо запаси вантажу у виробників, потреба споживачів і вартість перевезень задано наступною таблицією:
Таблиця 1.7.2
| Виробники | |||||
| Споживачі |
Рішення. Спочатку перевіряємо баланс між запасами виробників та потребою споживачів:
Запаси виробників - 18+40+12+8=78
Потреба споживачів – 20+15+35+8=78
Задача сбалансована. Будуємо нову таблицю і в її клітинки заносимо розмір партій вантажу, який треба перевезти. Формування партій починаємо з “північно-західного кута”. Перший виробник має запас 18 одиниць, а потреба споживача – 20, тобто перевішчує можливості виробника. Тому в першу клітинку заносимо – 18 і переходимо до наступного виробника. Він має запас в 40 одиниць, а незадоволеність споживача тількі 2 одиниці. Від другого виробника передаємо первому споживачу ці 2 одиниці і вважаємо, що потреба споживача задаволена повністю. Переходимо до другого споживача. Йому потрібно 15 одиниць, а виробника залишилось 38, тому повністю задовільняєм його потребу і переходимо до третього споживача. Третьому споживачу потрібно 35 одиниць, а у виробника залишилось 40-2-15=23 одиниці. Віддаємо 23 одиниці третьому споживачу. Так як його потреба залишилась не задовільненою 35-23=12 переходимо до третього виробника. Третій виробник має 12 одиниць, тому ми повністю задовольняємо потребу третього споживача. Залишилось нерозподілено 8 одиниць у четвертого виробника і 8 одиниць потрібно четвертому споживачу. Виконуємо останнє призначення.
Таблиця 1.7.3
| Виробники | |||||
| Споживачі |
Маючі таблицю вартості перевезень підрахуємо загальні витрати на перевезення за сформованим планом.
S = 18*20 + 2*15 + 15*4 + 23*22 + 12*12 + 8*12 = 1196.
В процесі виконання розподілу розглядається тільки запаси виробників і потреба споживачів. Метод “північно-західного кута” дозволяє легко створити план перевезень, але він не враховує вартість перевезень, тому його ефективність вкрай низька. Він може використовуватися тільке для побудови початкового плану перевезень і потребує подальшої оптимізації.
Пошук початкового розподілу постачань за методом “найменших витрат”. Метод “найменших витрат” є удосконаленям метода “північно-західного кута”. Перед розподілом також перевіряється баланс між постачальниками і споживачами.
Розподіл виконується за наступною схемою. Проводиться аналіз таблиці вартості транспортних витрат. Обірається постачання з мінімальною вартістю і виконуються його повне задаволення виходячі з можливостей постачальника і споживача. Далі знаходиться наступна клітинка з мінімальною вартістю і також виконується постачання. Процес завершується, якщо весь вантаж виробників буде розподілено відповідно потребам споживачів.
Приклад 1. Скласти план постачань для умов попереднього приклада методом “найменших витрат”.
Рішення. Спочатку аналізуємо таблицю вартості. Найменша вартість постачання дорівнює 4 і визначає вартість постачання від другого виробника другому споживачу. Потреба постачання 15 одиниць, а запас – 40. Після призначення цього перевезення другого споживача задоволено повністю, а у першого виробника залишилось 40-15=25 одиниць вантажу. Знаходимо наступну мінімальну вартість постачання. Вона дорівнює 5 і визначає постачання від першого виробника третьому споживачу. Так як потреба споживача (35) перевищую можливості виробника (18), то призначаємо перевезення всіх 18 одиниць від першого постачальника третьому споживачу. Наступна мінімальна вартість 5 відноситься до другого споживача, потреба якого вже задоволена. Далі вартість – 6. Це перевезення від третього виробника, який має 12 одиниць, четвертому споживачу, потреба якого 8 одиниць. Задовівльняємо цю потребу і у виробника залишається 12-8=4 одиниці вантажу. Наступна вартість 8, але перший виробник вже задовільнив повністю другого споживача. Далі – 12. Це постачання від третього виробника, до третього споживача. У третього виробника залишилось тільки 4 одиниці. Призначаємо їх. Інші 12 відносится до четвертого споживача, потреба якого вже задоволена. Наступна вартість –15 оцінює постачання від другого виробника першому споживачу. Задовільняємо його потребу. Після цього залишився не задоволеним третій споживач, тому залишки виробників надаємо йому.
Таблиця 1.7.4
| Виробники | |||||
| Споживачі |
Підрахуємо загальні витрати на перевезення за сформованим планом.
S = 15*4 +18*5 + 2*15 + 8*6+ 4*12+20*15 + 8*16 + 5*22 = 784.
Метод “найменших витрат” дозволяє отримати суттєве кращий результат, але він також не є оптимальним. Цей метод також застосовується для побудови початкового розподілу і краще наближає до оптимального плану постачань
Рішення транспортної задачі методом потенціалів. Існуєть багато методів розв’язування транспортних задач. Одним з таких методів є метод потенціалів. Сутність метода полягає у наступному.
Позначимо всіх постачальників через змінні Ui (i=1,m), а всіх споживачів через змінні Vj (j=1,n). Введемо поняття потенціалів. Потенціалами опорного рішення a будемо називати числа Ui і Vj таки, що сума Ui та Vj дорівнює вартості постачань відповідно для кожної клітинки Cij, яка заповнена за результатами початкового розподілу, тобто виконується рівнення Ui + Vj = Cij. Так як початковий розподіл має не менш одного зв’язку між постачальником і споживачем, то якщо встановити початкове значення Ui=0, то така система має рішення і всі значення Ui та Vj будуть знайдені.
По значенням Ui та Vj, які знайдені, розраховуваємо суми потенціалів для всіх не заповнених клетинок за формулою Ui та Vj. Якщо для всіх клетинок буде виконуватися співвідношення Ui + Vj £ Cij, то рішення, яке знайдено є оптимальним. В іншому випадку обіраємо клетинку в якої Ur + Vs > Crs. Якщо в транспортній таблиці провести перерозподіл призначень і включити цю клетинку, то план призначень може бути полипшено.
Для проведення перерозподілу в транспортній таблиці будуємо цикл, одно вершина якого знаходиться в клітинці i=r, j=s, а всі наступні вершини у заповнених клетинках, які є суміжними клітинці i=r, j=s. Кожній вершині присвоюємо “+”, або “-” у наступному порядку. В клетинці i=r, j=s встановлюємо “+”, суміжних клітинках “-”. При проведенні перерозподілу в клітинки зі знаком “+” переносимо повністю, або частково призначення, яке знаходиться в клітинці зі знаком “-” і так далі. Частка переноса призначення визначається можливостями виробника і потребою споживача.
Приклад 1. Скласти оптимальний план постачань для умов попередніх прикладів методом “потенціалів”.
Рішення. На підставі вихидних даних, які наведені в таблиці 1.7.5. За методом найменших витрат знаходимо початкове рішення. (Таблиця 1.7.6)
Для кожної заповненої клітинці створюємо рівняння Ui + Vj = Cij. В початковому плані постачань (Таблиця 1.7.6) заповнено 7 клітинок, тому будуємо систему з 7 рівнянь. Встановлюємо U1 = 0 і знаходимо всі значення Ui та Vj. Результати заносимо в таблицю 1.7.7. Розраховуваємо значення Ui + Vj для всіх не заповнених клітинок і також результати заносимо в таблицю.
| Таблиця 1.7.5 | Таблиця 1.7.6 | |
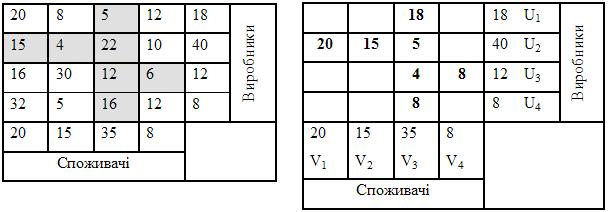
|
Таблиця 1.7.7
| Розрахунок потенціалів для заповнених клітинок | Розрахунок не заповнених клітинок | Значення Cij | Знак порівняння | |
| U1 +V3 = 5 U2 +V1 = 15 U2 +V2 = 4 U2 +V3 = 22 U3 +V3 = 12 U3 +V4 = 6 U4 +V3 = 16 | U1 = 0 U2 = 17 U3 = 7 U4 = 11 V1 = -2 V2 = -13 V3 = 5 V4 = -1 | U1 +V1 = -2 U1 +V2 = -13 U1 +V4 = -1 U2 +V4 = 16 U3 +V1 = 5 U3 +V2 = -6 U4 +V1 = 9 U4 +V2 = -2 U4 +V4 = 10 | £ £ £ > не викон. £ £ £ £ | |
Виконуємо порівнення знайдених сум зі значеннями Cij у відповідних клітинках на виконання умов Ui + Vj £ Cij. Таке співвідношення виконується практично для всіх сум за винятком U2 +V4 = 16, для якої C24 =10. Клітинка i=2, j=4 повина бути задіяна у розподілу постачань для поліпшення плану перевезень. Для перерозподілу перевезень будуємо цикл з вешиною в визначеній клітинці. Ставимо в цій клітинці “+”. Суміжними клітками які задіяни в початковому плане є клітинка i=2, j=3 та клітинка i=3, j=4. Ці клітинки є наступними вершинами циклу, тому в них ставимо “-”. Наступною суміжною клітинкою є клітинка i=3, j=3. Вона одночасно є суміжною двом попереднім клітинкам і завершує цикл. В цей клітинці ставимо знак “+”. Знаки “+” та “-” задають напрям перерозподілу призначень між клітинками, які входять до циклу. Результати визначення циклу наведені в таблиці 1.7.8.
| Таблиця 1.7.8 | Таблиця 1.7.9 | ||
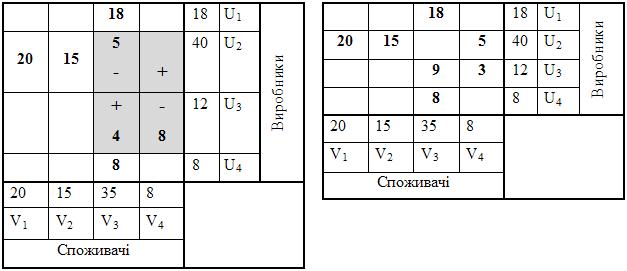
|
Виконаємо перерозподіл. Якщо перенести 8 одиниць з клітинки i=3, j=4 в клітинку i=2, j=4, тобто від виробника 3 до виробника 2, то для підтримки балансу навантаження на виробника треба 8 одиниць перенести в обратному напрямку далі по циклу. Але в клітинці i=2, j=3 є тільки 5 одиниць. Тому переносимо з клітинки i=3, j=4 в клітинку i=2, j=4 тільки 5 одиниць і відповідно з клітинки i=2, j=3 в клітинку i=3, j=3 теж 5 одиниць. За підсумками перерозподілу отримуємо новий план (таблиця 1.7.9.).
Розрахуємо і перевіримо потенціали нового плану постачань (таблиця 1.7.10).
Таблиця 1.7.10
| Розрахунок потенціалів для заповнених клітинок | Розрахунок не заповнених клітинок | Значення Cij | Знак порівняння | |
| U1 +V3 = 5 U2 +V1 = 15 U2 +V2 = 4 U2 +V4 = 10 U3 +V3 = 12 U3 +V4 = 6 U4 +V3 = 16 | U1 = 0 U2 = 11 U3 = 7 U4 = 11 V1 = 4 V2 = -7 V3 = 5 V4 = -1 | U1 +V1 = 4 U1 +V2 = -7 U1 +V4 = -1 U2 +V3 = 16 U3 +V1 = 11 U3 +V2 = 0 U4 +V1 = 15 U4 +V2 = 4 U4 +V4 = 10 | £ £ £ £ £ £ £ £ | |
За підсумками аналізу в даному розподілі немає ні жодної вільної клітинки з умовами Ur + Vs > Crs, тому даний розподіл є оптимальним. Вартість постачань за цім планом складає
S = 18*5 +20*15 + 15*4 + 5*10+ 9*12 + 3*6+ 8*16 = 754.
Методи рішення незбалансованої транспортної задачі. Якщо баланс між можливостями постачальників і потребою споживачів відсутній, то використовуваються методи доведення задачі до балансу.
Відсутність баланса може бути за рахунок залишкової або недостатньої можливості постачальників. При залишкової можливості постачальників серед них визначають тих, які дозволяють мати залишки і до початку розподілу заздалегліть їх визначають. За рахунок цього задача стає сбалансованою. Якщо немає можливості визначити постачальників, які дозволяють мати залишки, то штучно додають ще одного споживача, який сбірає всі нерозподілені надлишки. В таблиці вартості встановлюють розмір вартості складських витрат кожного постачальника. Якщо немає можливості визначити вартість складських витрат, то встановлюють вартість більшу ніж найбільша вартість постачань.
При недостатньої можливості постачальників серед споживачів обіраються ті, які дозволяють мати недопоставку у сумарному розмірі можливостей постачальників. За рахунок цього задача стає сбалансованою. Якщо немає можливості визначити споживачів, які дозволяють мати недопоставку, то штучно вводять додаткового постачальника, який буде задавільняти недопоставки. Ці недопоставки фактично задаволені не будуть, але недопоставки будуть розподіленні між споживачами оптимально. У цьому випадку до таблиці вартості постачань заносять максимально можливу вартість.
Після встановлення баланса транспортна задача вирішується звичайними методами.
Поиск по сайту: