 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Сучасні тенденції у розвитку засобів економіко-математичного моделювання
Складність економічних систем і велика кількість факторів, більшість з яких або суперечлива, або знаходиться в зоні ризику, або невизначена і потребує використання спеціальних методів моделювання світогосподарських процесів. Все більшего значення набуває необхідність використання якісних чинників, які не припускають числового вимірювання. Набуває розвитку методи врахування величин, які не мають чіткого уявлення і розглядаються як нечітки множини.
Задачі прийняття рішень. Будь-яка задача прийняття рішень характеризується наступними елементами:
Особа, що приймає рішення (ОПР) і повинна відповідати за наслідки цих рішень.
Множина змінних, значення яких вибираються ОПР. Будемо називати їх керуючими впливами або стратегіями.
Множина змінних, значення яких залежать від вибору стратегій. Їх будемо називати вихідними змінними (характеристиками прийняття рішень або исходами рішень).
Множина змінних, значення яких не регулюються ОПР. Ці змінні можуть залишатися певними при рішенні тієї або іншої задачі, і тоді їх називають параметрами задачі. В інших випадках вони можуть змінюватися незалежно від ОПР і тоді вони є збурюваннями (зовнішнім середовищем).
Задано інтервал часу Т, на якому приймається рішення в даній задачі (ситуації).
Математична модель задачі прийняття рішень, що являє собою множину співвідношень, які зв'язують стратегії (керуючий вплив) і параметри задачі з вихідними змінними.
Обмеження відображають вимоги, що накладаються ситуацією прийняття рішень на вихідні змінні й стратегії задачі.
Цільова функція (критерій оптимальності), що дає можливість оцінювати властивості обраного рішення. При цьому цільова функція може залежати від стратегій відповідно до математичної моделі задачі прийняття рішень.
Формалізація задачі прийняття рішень. Для формалізації задачі прийняття рішень введемо наступні позначення:
X - множина векторів стратегій;
P – множина векторів параметрів задачі;
W - множина векторів зовнішніх збурювань (стан зовнішнього середовища);
Y – множина векторів вихідних змінних.
Математична модель задачі прийняття рішень описується відображенням y вида:
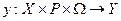 . (1.12.1)
. (1.12.1)
Залежно від виду відображення існують різні типи моделей. Так, залежно від ступеня мінливості параметрів і зовнішніх збурювань, моделі можуть бути статичними або динамічними. Якщо параметри P й зовнішні збурювання W не змінюються в часі, то математична модель буде статичною. У противному випадку, маємо динамічну модель ситуації прийняття рішень. Відображення y, що описує динамічну модель, може бути задано різними класами диференціальних і кінцево-різнисних рівнянь.
Математичні моделі різняться також видом зовнішніх збурювань, які можуть бути як детермінованими,так і випадковими.
Якщо збурювання невипадкові, то їх можна віднести до параметрів  задачі, і тоді детермінована модель буде описуватися відображенням виду
задачі, і тоді детермінована модель буде описуватися відображенням виду
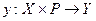 . (1.12.2)
. (1.12.2)
Якщо ж збурювання є випадковими, то маємо стохастичну модель задачі прийняття рішень, яка описується загальним відображенням (1.12.1). У цьому випадку вихідні змінні будуть також випадковими, їх розподіл при заданих параметрах P будуть визначатися розподілами зовнішніх збурювань.
Залежно від умов зовнішнього середовища й ступеня інформованості особи, яка приймає рішення, існує така класифікація завдань прийняття рішень: а) в умовах визначеності; б) в умовах ризику; в) в умовах невизначеності; г) в умовах конфліктних ситуацій або протидій (активного супротивника).
Прийняття рішень в умовах визначеності Прийняття рішень в умовах визначеності характеризується однозначним або детермінованим зв'язком між прийнятим рішенням і його результатом. Головні труднощі – це наявність багатьох критеріїв, по яких варто порівнювати результати. Тоді виникає проблема прийняття рішень при так званому векторному критерії оптимальності. Рішення багатокритеріальних задач знаходиться в кружині деякої оптимальної точки. Сукупність значінь всіх критеріїв, які складають оптимальне рішення зветься Парето множиною.
Прийняття рішень в умовах ризику. Задача виникає у тому випадку, коли з кожною стратегією xi пов’язана множина можливих результатів { y1, y2,…,yn }, кожен з яких має свою корисність { ui1, ui2,…,uin }. Для кожного результату визначена ймовірність P(yj(xi)). Формально модель задачі можна уявити у вигляді матриці:
 ,
,
де: uij – корисність результату yj при використанні стратегії xi.
| Таблиця 1.12.1 Таблиця рішень в умовах ризику | ||||||
| y1 | y2 | … | yj | … | yn | |
| x1 | u11 | u12 | … | u1j | … | u1n |
| … | … | … | … | … | … | … |
| xi | ui1 | ui2 | … | uij | … | uin |
| … | … | … | … | … | … | … |
| xm | um1 | um2 | … | umj | … | umn |
Хай апріорно визначені умовні ймовірності P (yj|xi), i = 1,m, j = 1,n. Запровадимо очікувану корисність для кожної стратегії:


Правило визначення оптимальної стратегії:
 , (1.12.3)
, (1.12.3)
Поиск по сайту: