 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Неоклассические теории экономического роста
Неоклассические модели экономического роста разрабатывались на основе использования производственных функций, т.е. функций, устанавливающих зависимость между выпуском продукции и факторами производства. Обычно исследователи исходят из предпосылки эффективною использования факторов. Например, из всего множества комбинаций труда и капитала, удовлетворяющих бюдже1-ным возможностям фирмы, анализ останавливается на
множестве комбинаций факторов, соответствующих полному использованию бюджета (граничная линия на графике бюджетных возможностей фирмы).
Производственная функция. Рассмотрим производственную функцию в общем виде Y = f (К, L) и определим свойства производственных функций. Производственная функция строится таким образом, чтобы удовлетворить следующим гипотезам (временно абстрагируемся от технического прогресса).
1. Непрерывность. Функции являются непрерывными и превращаются в нуль, когда один из производственных факторов превращается в нуль:
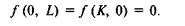
2. Аддитивность. Это означает, что объединение усилий двух групп (L1,K1) и (L2, K2) даст результаты по меньшей мере такие же хорошие, как и результаты, достигнутые при раздельном производстве этих групп; кооперация групп не может дать худшие результаты:

3. Делимость. Гипотеза делимости означает, что любой производственный процесс может осуществляться в сокращенных масштабах. Из закона падающей предельной производительности факторов производства при росте его объемов следует:
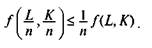
Используя указанные три гипотезы, можно вывести некоторые важные свойства производственных функций.
Свойство 1. Постоянная отдача.
Удвоение факторов производства, например, приводит к удвоению выпуска продукции:
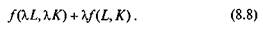
Если опустить гипотезы 2 и 3, то кроме постоянной отдачи можно было бы получить возрастающую и убывающую отдачу:
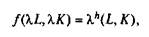
возрастающая отдача при h > 1; постоянная отдача при h = 1; убывающая отдача при h < 1.
При постоянной отдаче выражение Y = f(K, L) можно заменить следующим уравнением:
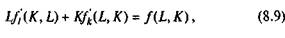
где fI' и fk' есть предельная отдача труда и капитала.
Используя свойство постоянной отдачи, можно свести функцию f(L, К) к функции с одной переменной, записав ее в виде:
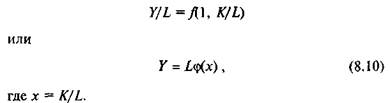
Свойство 2. Падение предельной производительности.
Это свойство известно из экономической теории: когда один фактор из двух увеличивается, то его предельная производительность снижается (свойство постоянной отдачи соблюдается при увеличении двух факторов в одинаковой пропорции).
Производственная функция Кобба-Дугласа — это производственная функция, которая учитывает совокупность двух основных факторов производства — капитала и труда — и обладает установленными выше свойствами. В соответствии с общим свойством всех производственных функций данная функция предполагает полное использование, капитала и полную занятость.
Функция Кобба-Дугласа была введена двумя американскими экономистами — Ч. Коббом и П. Дугласом — для изучения замены факторов «труд-капитал»:
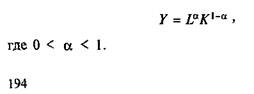
Функция может быть переписана в виде
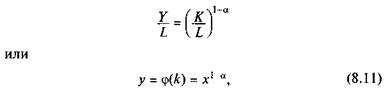
|
где у = Y/L; к = K/L.
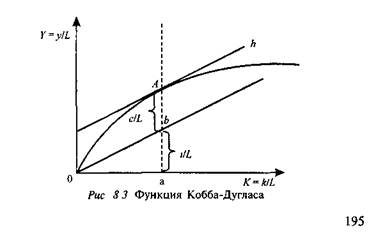
Графическое изображение функции Кобба-Дугласа в форме (8 11) представлено на рисунке 8 3
Рассмотрим произвольную точку А функции, касательную к этой точке и прямую Ob, проведенную через начало координат параллельно касательной. Тогда:

|
Поскольку прямая Ob параллельна касательной, то можно показать, что отрезок аА разбивается прямой Ob пропорционально доле труда (bА) и капитала (ab) в выпуске.
Рассмотрим эластичность замены в функции Кобба-Дугласа Поскольку изокванты (кривые, точки которых есть сочетание L и К, для которых производственная функция принимает одни и те же значения) представляют собой непрерывные кривые, замена возможна при условии
У = LaK1-a = const.
Кроме того, при замещении факторов должны сохраняться пропорции их долей в выпуске. Отсюда следует, что эласшчность замены в функции Кобба-Дугласа равна еде-нице1.
Отношение а/(1-а) в функции Кобба-Дугласа остае1-
ся постоянным. Если, например, а = 0,3, то вклад труда в Y составляет 30%
Существует еще один фактор, помимо труда и капитала, коюрый вызывает рост производства, — технический прогресс. Этот термин отражает не только технологическое обновление производства на основе использования более производительной техники или новых материалов, но и все дру1ие причины, которые влияют на отдачу труда и капитала (более совершенная организация труда, улучшение качества рабочей силы, улучшение отраслевой структуры производства, повышение эффективности государ-С1венною управления и пр).
В производственной функции технический прогресс задастся экзогенным параметром:
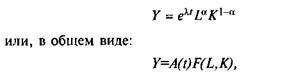
где параметр (лямда) или A(t) задает постоянный во времени темп роста выпуска, вызванный техническим прогрессом Модель экономического роста Р. Солоу. Неоклассиче ские модели роста начали разрабатываться в 50-х гг. про шлого века, когда на первый план вышла проблема достижения экономического роста не столько за счет неиспользо
Юг эластичности замены следует отличать эластичность выпуска Последняя показывает, насколько изменится значение функции при изменении используемого фактора на единицу и измеряется как производная функции по данному фактору Если бы мы взяли линейную производственную функцию с линейной изоквантои, то эластичность выпуска была бы величиной постоянной для каждой точки изокванты Но эластичность замены в этом случае была бы различной, поскольку при расчете данного показателя используются не только отношения эластичностеи выпуска, но и абсолютные значения факторов в рассматриваемой точке изокванты.
ванных мощностей, сколько за счет технического прогресса. Методологической основой их моделей осталась классическая теория факторов производства и предельной производительности.
Представители неоклассической школы критиковали кейнсианцев за игнорирование других факторов, кроме накопления капитала, за рассмотрение капиталоемкости выпуска как величины постоянной, за их недооценку способности рынка восстановить равновесие. В отличие от неокейнсианцев они считали, что только свободная рыночная экономика может обеспечить сбалансированность экономического роста. Помимо рыночного механизма, вторым условием возможности поддержания равновесного роста они считали устойчивость денежной системы. Поэтому неоклассики выступали против инфляционных государственных расходов, которые рекомендовали правительствам кейнсианцы в период кризисов, й рассматривали такие расходы, как фактор нестабильности.
В 1956-1957 гг. Р. Солоу опубликовал статьи, в которых предложил свою модель экономического роста. В 1957 г. ему было присуждена Нобелевская премия по экономике.
В модели Р. Солоу выпуск продукции - функция не только капитала, но и труда, которые являются хорошими субститутами, и сумма коэффициентов эластичности выпуска по этим факторам равна единице. Другие предпосылки модели — убывающая предельная производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия капитала, отсутствие инвестиционных лагов. Сначала модель описывает как система приходит в равновесие при отсутствии учета технического прогресса (т.е. при нейтральности технического прогресса) и постоянной отдаче от масштаба, затем в нее вводятся технологические сдвиги посредством изменения нормы накопления капитала и убывающей отдачи от масштаба.
В модели используется производственная функция Коб-ба-Дугласа в форме (8.11). Графическое представление данной функции дано на рис. 8.3. График показывает, что капиталовооруженность к определяет размер выпуска в расчете на одного работника. Тангенс угла наклона касательной h равен предельной производительности капитала: если к увеличивается на одну единицу, то у возрастает на МРК
единиц. По мере роста капиталовооруженности труда его производительность возрастает со снижающейся скоростью.
Модель описывается следующими уравнениями, выражающими зависимость между экономическими показателями в пересчете на одного работника:
y=f(k) - совокупное предложение;
у = с + i = (i — s)y + i = i/s — спрос. Здесь с и i -потребление и инвестиции, s — норма сбережения;
f(k) = i/s — равенство спроса и предложения;
i = sf(k) — инвестиции на одного работника. Они зависят от капиталовооруженности и нормы накопления. Норма накопления определяет деление продукта на инвестиции и потребление при любом значении к. Поэтому чем выше к, тем выше уровень производства и больше инвестиции, т.е. существует связь между накопленным запасом капитала и накоплением нового капитала, что иллюстрирует рисунок 8.4;
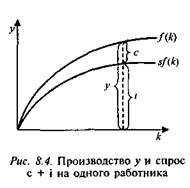
Ак = I - dk = sf(k) — dk — прирост запаса капитала на одного занятого. Запас капитала изменяется в случае, когда его выбытие dk вследствие износа капитала (d — норма амортизации) не равно инвестициям. Величина выбытия пропорциональна накопленному капиталу. На рис. 8.5 эта связь отражается прямой, выходящей из точки начала координат с угловым коэффициентом, d.
Запас капитала (к) будет расти (Ak: > 0) до уровня, при котором инвестиции будут равны величине выбытия. Затем величины выбытия и инвестиций уравновесят друг друга (Ак =0). Уровень запаса капитала, при котором
|
|
инвестиции равны выбытию, называется равновесным (устойчивым) уровнем капиталовооруженности труда (к*).
11ри достижении k* экономика находится в состоянии долгосрочного равновесия.
Независимо от первоначального накопления капитала, с которого начинает развиваться экономика, она затем приходит в состояние равновесия. Если запасы капитала (k1) ниже устойчивого уровня, валовые инвестиции превышают выбытие (dk), запас капитала будет расти на величину чистых
инвестиций и приблизится к к*. Если запасы капитала (к2) выше к*, то произойдет обратный процесс. В точке равновесия валовые инвестиции станут равными выбытию, а чистые инвестиции Л к будут равны нулю.
На равновесный уровень капиталовооруженности влияет норма накопления (сбережения). Рост нормы сбережения с s1 до s2 сдвигает кривую инвестиций вверх из положения s1f(k) до S2f(k) (см. рис. 8.6). При этом экономика переходит в новое состояние долгосрочного равновесия. Более высокая норма сбережения обеспечивает больший запас капитала и более высокий уровень производства. Страны с более высокой долей инвестиций в ВВП имеют и более высокий уровень жизни.
По процесс накопления в результате повышения нормы сбережения не объясняет механизм непрерывного экономического роста, а лишь показывает переход экономи-
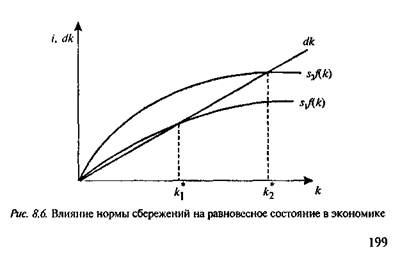
ки из одного равновесного состояния в другое. Поэтому Р Солоу развивает модель и вводит в нее факторы технического прогресса и роста численности населения.
Равновесный уровень капиталовооруженности при росте населения. Пусть население растет с постоянным темпом п Гели при этом другие условия не изменяются, то рост населения будет всс1и к снижению капиталовооруженности труда Теперь уравнение, показывающее изменение запасов капитала на одного работника, будет выглядеть.

Па поддержание капиталовооруженности при росте численности населения необходим такой объем инвестиции, коюрый не только покрывал бы выбытие капитала, но и обеспечивал бы капиталом новых работники. Произведение пк показывает, сколько требуется дополнительного капитала в расчете на одного занятого, чтобы капиталовооруженность увеличившегося количества работников не отличалась от уровня до повышения численности занятых
Уравнение, формализующее условие сохранения устойчивою равновесия в экономике при росте занятости, выглядит как

Это означает, что инвестиции sf{k) должны компенсировать и выбытие капитала, и рост населения. Но из постоянства капиталовооруженности при росте населения следует, что капитал должен возрастать с тем же темпом, что и население, т.е. AY /Y= AL/L= АК/К
Отсюда следует, что рост населения вызывает эконо мический рост в условиях устойчивого состояния экономики Но если рост населения не сопровождается увеличс нием инвестиции, то это ведет к уменьшению капитало емкости и уменьшению душевого дохода (рис. 8 6)
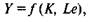
|
| 1де е — эффективность труда; Le — численность условных единиц труда с постоянной эффективностью. |
Учет в модели Р Солоу технического прогресса. 1 ретьи м исючником экономического роста после инвестиций и роста занятых является технический прогресс Включение технического прогресса в производственную функцию при водит ее к следующему виду:
Технический прогресс проявляется в приросте эффективности труда с постоянным темпом g. Такая форма технического прогресса называется трудосберегающей, a g — темпом грудосберегающего технического прогресса. Если, например, g = 0,02, то отдача от каждой единицы труда увеличится на 2% в год. Эго равносильно росту численности занятых на 2%. Например, в текущем году 100 рабочих могут произвести столько продукции, сколько в предыдущем году производили 102 рабочих. Или, по другому, можно считать, что в базовом году Le = 100, а в следующем году, когда наблюдался технический прогресс, Le = 102 ра-6oiпикам, производительность которых осталась на уровне базовот юда.
Таким образом, технический прогресс может быть отражен в модели аналогично росту населения, но без снижения уровня капиталовооруженности. Уравнение, выражающее в равновесной точке равенство между объемом инвеешций и выбытием части ранее накопленного капитала, выглядит теперь следующим образом:
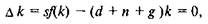
где g — темп технического прогресса, который как будто приводит к более быстрому обесцениванию действующего оборудования.
В новом устойчивом состоянии (к1*) общий объем ка-
пшала К и выпуска Y будет расти с темпом (п + g). Но в отличие от случая роста населения теперь с темпом g будут расти капиталовооруженность (K/L) и выпуск (Y/L) в расчете на одного занятого. Это означает, что технический прогресс в модели Р. Солоу является единственным условием непрерывного экономического роста и роста уровня жизни, поскольку лишь при его наличии происходит устойчивый рост выпуска на душу населения.
В модели Р Солоу норма сбережения s является экзогенным фактором При любом заданном s экономическая система приходит со временем в некоторое состояние равновесия, которое характеризуется своим уровнем выбы-шя капитала и, следовательно, уровнем потребляемого дохода. Модель Солоу помогает найти тот уровень сбережений, который позволяет максимизировать потребляемый доход. Условие, при котором достигается максимальный
уровень потребления, американский экономист Э. Фелпс в работе «Басня для тех, кто занимается ростом» (1961) назвал «золотым правилом» накопления. В устойчивом состоянии
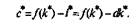
где с* - потребление в устойчивом состоянии.
В соответствии с «золотым правилом» уровень потребления будет самым высоким при достижении наибольшей
разницы между объемом выпуска f(k*)и объемом выбытия dk* в условиях устойчивого уровня капиталовооруженности, когда dk* = I*. Потребление в этом случае называется устойчивым уровнем потребления:
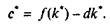
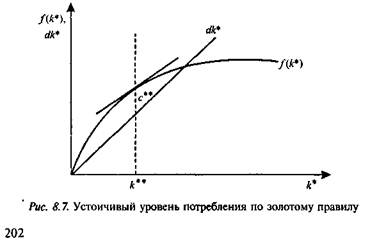
Запас капитала, который обеспечивает устойчивое состояние при таком потреблении, называется «золотым уровнем» накопления капитала (к**)- На рис. 8.7 показано, как можно найти с** и к** графическим способом. При уровне
капиталовооруженности к**, соответствующем «золотому правилу», выполняется условие МРК = d (предельный продукт капитала, равный норме выбытия), а с учетом роста населения и технического прогресса
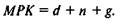
|
|
На основании результатов, полученных из анализа модели Солоу, неоклассики дали несколько рекомендаций для разработчиков экономической политики. Норму сбережения следует увеличивать или уменьшать в зависимости от отношения фактического запаса капитала по отношению к запасу капитала, рекомендуемого в соответствии с «золотым правилом».
Если, например, экономика начинает развиваться с меньшей капиталовооруженностью, чем при устойчивом состоянии по «золотому правилу», то необходимо увеличить норму сбережений. В этом случае повысятся инвестиции и снизится потребление, но по мере накопления капитала с некоторого момента потребление начнет снова расти. Экономика достигнет нового равновесного состояния, при котором в соответствии с «золотым правилом» потребление будет иметь более высокий уровень.
Поскольку единственным фактором долгосрочного экономического роста, как следует из модели Р. Солоу, является технический прогресс, правительства многих стран мира проводят государственную политику по его стимулированию, используя различные инструменты.
Рассмотренная модель не лишена недостатков. Как любое формальное описание, она содержит много упрощающих предпосылок; некоторые экзогенные переменные следовало бы не задавать до исследования, а находить в процессе исследований, т.е. делать эндогенными; не учитываются некоторые важные ограничители роста, например, экологические и т.д. Эти и другие недостатки пытаются преодолеть современные теории экономического роста.
ЛИТЕРАТУРА
1. Ивашковский С. Н. Макроэкономика. — М., 2002.
2. Аукционек СП. Современные буржуазные теории и модели цикла (критический анализ). — М, 1984.
3. Столеров Р. Равновесие и экономический рост. — М., 1974.
4. Агапова Г. А., Серегина С. Ф. Макроэкономика. - 4-е изд. — М., 2001.
5. Экономическая теория / Под ред. И.В. Новиковой. — Мн., 2006.
Поиск по сайту: