Розв 'язания

Крок 1. Нормалізація змінних.

Позначимо вектори незалежних змінних — продуктивності праці, фондомісткості, коефіцієнтів плинності робочої сили — через x₁, x₂, x₃. Елементи стандартизованих векторів обчислимо за формулою:

,

де n — кількість спостережень, n =10; m — число незалежних змінних, m =3; — середнє арифметичне значення вектора x_k; 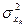— дисперсія змінної x_k.

Із формули бачимо, що спочатку потрібно обчислити середні арифметичні для кожної пояснювальної змінної:

; ;

.

Усі розрахункові дані для стандартизації змінних x₁, x₂, x₃ згід­но з поданими співвідношеннями наведено в табл. 2.

2.Розрахунок нормалізованих змінних

№п/п
	3,3 0,3 1,3 2,3 -3,7 5,3 0,3 -4,7 -8,7 4,3	0,274 -0,186 0,084 -0,006 -0,106 -0,106 0,034 -0,186 -0,106 0,304	4,69 0,79 -1,31 -5,31 8,69 -2,31 2,69 -0,31 -0,31 -7,31	10,89 0,09 1,69 5,29 13,69 28,09 0,09 22,09 75,69 18,49	0,075076 0,034596 0,007056 0,000036 0,011236 0,011236 0,001156 0,034596 0,011236 0,092416	11,56 2,56 0,16 19,36 92,16 1,96 12,96 0,36 0,36 40,96	0,2487 0,0226 0,0980 0,1733 -0,2788 0,3994 0,0226 -0,3541 -0,6556 0,3240	0,0091 -0,3531 0,2580 0,0543 -0,1720 -0,1720 0,1448 -0,3531 -0,1720 0,7559	-0,2518 0,1185 -0,0296 -0,3258 0,7108 -0,1037 0,2666 0,0444 0,0444 -0,4739
Σ				176,1	0,278640	182,4

Дисперсії кожної незалежної змінної мають такі значення:

; ;

.

Тоді знаменник для стандартизації кожної незалежної змінної буде такий:

;

;

.

Матриця стандартизованих змінних подається у вигляді:

Крок 2. Знаходження кореляційної матриці:

,

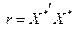де X^* — матриця нормалізованих пояснювальних змінних; — матриця, транспонована до матриці X^*.

Ця матриця симетрична і має розмір 3x3.

Для даної задачі

Кожний елемент цієї матриці характеризує тісноту зв'язку однієї незалежної змінної з іншою. Оскільки діагональні елементи харак­теризують тісноту зв'язку кожної незалежної з цією самою змінною, то вони дорівнюють одиниці. Зауважимо, що при знаходженні добу­тку матриць і X^* за рахунок зміщеності коефіцієнтів парної ко­реляції числові значення діагональних елементів можуть наближа­тись до одиниці. Якщо це так, то вони заміняються одиницями, а інші значення матриці r збільшуються на величину, що визначається як різниця між одиницею і діагональним елементом.

Інші елементи матриці r дорівнюють:

;

;

,

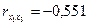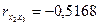тобто вони є парними коефіцієнтами кореляції між пояснювальними змінними. Користуючись цими коефіцієнтами, можна зробити ви­сновок, що між змінними x₁, x₂, x₃ існує зв'язок. Але чи можна стверджувати, що цей зв'язок є виявленням мультиколінеарності, а через це негативно впливатиме на оцінку економетричної моделі?

Щоб відповісти на це запитання, потрібно ще раз звернутися до алгоритму Фаррара—Глобера і знайти статистичні критерії оцінки мультиколінеарності.

Крок 3. Обчислимо детермінант кореляційної матриці r і кри­терій χ ²:

а) ;

б) .

При ступені вільності =3 і рівні значущості α=0,01 критерій χ²_табл.=11,34. Оскільки χ²_факт <χ²_табл., робимо висновок, що в масиві пояснювальних змінних не існує мультиколінеарності.

Крок 4. Знайдемо матрицю, обернену до матриці r:

;

.

Крок 5. Використовуючи діагональні елементи матриці С, обчи­слимо F -критерії:

;

;

.

Для рівня значущості α = 0,05 і ступенів вільності γ₁ = 7 і γ₂ = 2 критичне (табличне) значення критерію F = 4,74.

Оскільки

F _1факт< F _табл;

F _2факт< F _табл;

F _3факт< F _табл,

то кожна з пояснювальних змінних немультиколінеарна з двома іншими.

Щоб визначити наявність попарної мультиколінеарності, про­довжимо дослідження і перейдемо до кроку 6.

Крок 6. Обчислимо частинні коефіцієнти кореляції, скористав­шись елементами матриці С:

Частинні коефіцієнти кореляції характеризують тісноту зв'язку між двома змінними за умови, що третя не впливає на цей зв'язок.

Порівнявши частинні коефіцієнти кореляції з парними, які було наведено раніше, можна помітити, що частинні коефіцієнти значно менші за парні. Це ще раз показує, що на підставі парних коефіцієнтів кореляції не можна зробити висновків про наявність мультиколінеар­ності чи її відсутність.

Крок 7. Визначимо t -критерій на основі частинних коефіцієнтів кореляції.

;

;

.

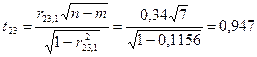Табличне значення t -критерію при n-m = 7 ступенях вільності і рівні значущості α = 0,05 дорівнює 1,69. Усі числові значення t -критеріїв, знайдених для кожної пари змінних, менші за їх таблич­ні значення. Звідси робимо висновок, що всі пари незалежних змін­них не є мультиколінеарними.

Отже, усі пояснювальні змінні досліджуваної моделі не мультиколінеарні.

Якщо F -критерій більший за табличне значення, тобто коли k-та змінна залежить від усіх інших у масиві, то необхідно вирішувати питання про її вилучення з переліку змінних.

Якщо t_kj — критерій більший за табличний, то ці дві змінні (k і j) тісно пов'язані одна з одною. Звідси, аналізуючи рівень обох видів критеріїв F і t, можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.

Найпростіше позбутися мультиколінеарності в економетричній моделі можна, відкинувши одну зі змінних мультиколінеарної пари. Але на практиці вилучення якогось чинника часто суперечить логіці економічних зв'язків. Тоді можна перетворити певним чином пояс­нювальні змінні моделі:

а) узяти відхилення від середньої;

б) замість абсолютних значень узяти відносні;

в) стандартизувати пояснювальні змінні тощо.

За наявності мультиколінеарності змінних потрібно звертати увагу й на специфікацію моделі. Іноді заміна однієї функції іншою, якщо це не суперечить апріорній інформації, дає змогу уникнути явища мультиколінеарності.

Коли жодний з розглянутих способів не дає змоги позбутися мультиколінеарності, то параметри моделі слід оцінювати за мето­дом головних компонентів.

Поиск по сайту: