Перевірка моделі на адекватність за критерієм Фішера

1. Сучасні методи управління економічними системами та процесами базуються на широкому використанні математичних методів та ЕОМ.

На сучасному етапі економічна наука сягнула високих рубежів у своєму розвитку і розглядає задачі, для розв’язування яких недостатньо використовувати традиційні економічні методи, тому математика займає в економіці одне з провідних місць. Сформувався напрям – економіко-математичне моделювання. Математичне моделювання є вираженням процесу математизації наукового економічного знання. Основним поняттям є математична модель.

Математична модель об’єкта містить у собі 3 групи елементів:

1) характеристику об’єкта, яку потрібно визначити (невідомі величини) – вектор Y=(y_j);

2) характеристики зовнішніх щодо модельованого об’єкта умов, які змінюються – вектор Х=(х_j);

3) сукупність внутрішніх параметрів об’єкта − А.

Множини умов Х і параметрів А розглядаються як екзогенні величини (такі, що визначаються поза рамками моделі), а величини, що належать вектору У – ендогенні (такі, що визначаються за допомогою моделі).

Математичну модель можна розуміти як перетворювач зовнішніх умов об’єкта У (виходу), які мають бути знайдені.

Математичні моделі поділяють на дві групи:

- структурні;

- функціональні.

Вивчення структурних моделей дає одночасно цінну інформацію про поводження об’єкта. Структурні моделі розкривають внутрішню організацію об’єкта: його складові частини, внутрішні параметри, їх зв’язок з входом і виходом. Є три види структурних моделей:

1) y_j = f_j(A,X) – явні функції від зовнішніх умов Х і внутрішніх параметрів А;

2) ψ_і (А,Х,Y)=0 – неявні функції, всі невідомі визначаються одночасно із системи рівнянь;

3) імітаційні моделі – конкретний вигляд співвідношень невідомий.

Моделі типу (1) і (2) можна розв’язати за допомогою чисельних алгоритмів.

Імітаційні моделі не зводяться до чітко визначених математичних задач і тому їм належить проміжне місце між структурними і функціональними моделями.

Основна ідея функціональних моделей – пізнання суті об’єкта через його поведінку, діяльність, функціонування.

Функціональна модель описує поводження об’єкта так, що задаючи значення входу Х можна отримати значення виходу Y без участі інформації про параметри:

Y = A(X),

де A – оператор, який пов’язує Х і Y.

При вивченні функціональних моделей необхідно сформулювати гіпотезу про внутрішню структуру об’єкта.

Економетричні моделі належать до функціональних моделей. Вони кількісно описують зв’язок між вхідними показниками економічної системи (Х) та результативним показником (Y).

У загальному вигляді економетричну модель можна записати так:

y=f(x;u),

де x – вхідні економічні показники; u – випадкова або стохастична складова.

Показники Х найчастіше бувають детермінованими, тобто не залежать від впливу випадкових факторів.

Складова u – випадкова змінна, але оскільки залежна змінна Y залежить від u, то вона є теж стохастичною, описує кореляційно- регресійний зв’язок між економічними величинами.

Отже, для побудови економетричної моделі необхідно:

1) мати досить велику сукупність спостережень даних;

2) забезпечити однорідність сукупності спостережень;

3) забезпечити точність вхідних даних.

2.Сукупність спостереження розглянута в теорії статистики. Слід розрізняти джерело даних – одиницю спостереження та одиницю сукупності. Під час перепису: одиниця спостереження − сім’я, а одиниця сукупності – окрема людина. Ці поняття часто збігаються. Тому в економетрії здебільшого йдеться про одиницю сукупності.

Нехай Х – певна ознака спостеження, то Х_ij^t або Х_ijt означає j ознаку і – го спостереження в період t, (i=1;m), (j=1;n), (t=1;T):

n – число одиниць сукупності;

m – число ознак, які описують кожну одиницю;

T – проміжок часу, за який вивчається ознака певного спостереження.

За одиницю сукупності часто беруть певний економічний об’єкт, що функціонує – технологічний агрегат, цех, підприємство, галузь, людину, тварину.

Існує три способи формування вибірки:

- часова, коли розглядається функціонування окремого об’єкта в динаміці;

- просторова, коли сукупність спостережень вивчається у статиці;

- просторово-часова – комбінація просторової і часової вибірки.

3. Економічні сукупності як правило неоднорідні. Поняття однорідності сукупності спостережень охоплює якісну і кількісну однорідність. Під якісною розуміють однотипність економічних об’єктів, їх однакову якість та призначення, а під кількісною – однорідність групи одиниць спостережень, що визначається на основі кількісних оцінок.

Кількісна однорідність можлива лише за наявності одноякісності явищ та процесів, що утворюють сукупність спостережень, тобто ці поняття однорідності діалектично взаємопов’язані.

Дані вхідної сукупності спостережень повинні мати:

- однаковий ступінь агрегування;

- однорідну структуру одиниць сукупності;

- однакові методи розрахунку показників у часі;

- однакову періодичність обліку окремих змінних;

- порівнянні ціни та однакові інші зовнішні економічні умови.

4. При економічних розрахунках постає питання про точність (помилки) економічних показників. Помилки показників виникають при побудові алгоритму розрахунку, формуванні даних, у процесі обчислення. Усі помилки поділяють на систематичні і випадкові.

Систематичні помилки мають або постійну величину або змінюються за певною функціональною залежністю. Вони є однонапрямленими і можуть бути істотними за величиною.

Випадкові помилки зумовлюються впливом випадкових чинників при формуванні показників. При формуванні сукупності спостережень для економетричних моделей слід звертати увагу на можливість існування помилок саме у вхідних даних.

5.При економетричному моделюванні треба добре знати об’єкт дослідження, а саме:

- визначити набір змінних, що описують процес функціонування досліджуваних об’єктів;

- проаналізувати взаємозв’язки між окремими змінними;

- вибрати раціональний тип економетричної моделі.

Вибір результативних ознак вирішується, виходячи з мети дослідження. Вибір незалежних змінних є процесом уточнення початкової гіпотези. У цьому процесі можна вирізнити такі етапи:

- формування початкової гіпотези про набір незалежних змінних;

- експертна оцінка цього набору;

- аналіз взаємозв’язків;

- добір і звуження кола істотних для моделювання змінних.

6. Розглянемо економетричну модель з двома змінними у загальному вигляді:

y = f(x) + u,

де у – залежна змінна; x – незалежна змінна; u – випадкова складова. Це проста економетрична модель.

Одні і ті самі економічні процеси можна описати різними функціями, але за допомогою статистичного аналізу потрібно вибрати одну.

Найпростіша форма зв’язку між двома змінними лінійна:

y = a₀ + a₁x,

де a_0, a₁ – невідомі параметри.

Можливі й інші форми залежностей між двома змінними. Як правило нелінійні функції зводять до лінійних шляхом логарифмування або заміни:

y = a₀e^a1x, lny = ln a₀ + a₁x;

y = a₀x^a1, lny = ln a₀ + a₁lnx, ln x = z;

y = a₀ + a_1/x, 1/x = z,y = a₀ + a₁z;

y = α(1-r)^x, lny = lnα + xln(1-r);

y = e ^{a0 + a1x}, lny = a₀ + a₁x;

y = 10 ^{a0 + a1x}, lgy = a₀ + a₁x.

Нехай ми вибрали якусь із цих залежностей, визначили невідомі параметри і одержали рівняння регресії.

Як відомо певна частина фактичних спостережень над змінною лежатиме вище або нижче від значень, обчислених згідно з вибраною функцією. А це свідчить про те, що вибрана функція не адекватна реальному процесу взаємозв’язків у економіці. Щоб розв’язати цю задачу, до економетричної моделі вводять стохастичну (випадкову) складову, яка акумулює в собі всі відхилення фактичних спостережень змінної у від обчислених згідно з моделлю:

y = a₀ + a₁x +u.

Стохастичну складову u економетричної моделі називають похибкою (залишком, збуренням, відхиленням).

У класичній лінійній економетричній моделі змінна u інтерпретується як випадкова змінна, що має розподіл з середньою величиною, яка дорівнює нулю і сталою дисперсією Ơ_u². Оскільки u охоплює вплив багатьох факторів, які є незалежними, то згідно з центральною граничною теоремою теорії ймовірності можна зробити висновок, що стохастична (випадкова) складова економетричної моделі розподілена за нормальним законом.

Щоб оцінити параметри моделі, потрібно сформувати сукупність спостережень, кожна одиниця якої характеризується відповідними значеннями (х;у).

Нехай побудували кореляційне поле точок (х;у), через які можна провести безліч прямих ліній y = a₀ + a₁x (рис. 1).

у

· · · · · · · · · ·

· · · · · · · · ·

· · · ·.· · · · · · · ·

.· · ·

· · · ·· ·· · · ···

· · · · · ·

· · · ·

0х

Рис. 1.Кореляційне поле точок

Вони різняться між собою параметрами a₀ і a₁. Треба вибрати ту лінію, для якої б відхилення фактичних у від розрахункових ŷ було б найменшим.

Принцип найменших квадратів відхилень полягає в знаходженні таких â₀ і â₁, для якої Σu_i² була б найменшою (ŷ= â₀ + â₁х −для розрахункових).

S = Σu_i² = Σ (y_i - ŷ_i) ² = Σ (y_i - â₀ - â₁х)² → min.

∂S nâ₀ + â₁∑х_i =Σ y_i;

∂a₀ = -2∑(y_i - â₀ - â₁х) = 0;

∂S â₀ ∑х_i + â₁∑х_i ²= Σ y_iх_i;

∂a₁ = -2∑(y_i - â₀ - â₁х) x_i=0;

.

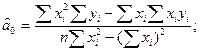
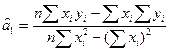Оцінки параметрів â₀ і â₁ за методом найменших квадратів такі, що лінія регресії обов’язково проходить через точку (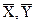), тобто = â₀ + â_{1 .}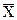

Є ще інший альтернативний спосіб обчислення параметрів â₀ і â₁ :

â₁ =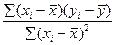

де â₀ знаходиться з рівняння:

â₀ = - â₁ .

За нашим прикладом = 1008/10=100,8, = 542/10=54,2.

Приклад. Побудувати економетричну модель залежності витрат ресурсів на одиницю продукції (у) від рівня фондомісткості продукції (х) (дані в умовних одиницях). Розрахунки проводимо в табл.1.

Запишемо систему нормальних рівнянь:

nâ₀ + â₁∑х_i =Σ y_i; 10â₀ + â₁1008 = 542;

â₀ ∑х_i + â₁∑х_i ²= Σ y_i x_i; 1008â₀ + â₁104784= 56221;

â₀ = = = =3,84;

â₁= = = 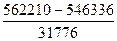=0,4993≈0,5.

Економетрична модель має вигляд (для фактичних значень незалежної змінної)

Y = 3,8 + 0,5 x + u.

Скориставшись альтернативним способом обчислення за допомогою відхилень середніх арифметичних, одержимо:

â₁ = = =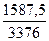0,4702≈0,5,

де â₀ знаходиться з рівняння:

â₀ = 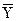- â₁ х = 54,2 – 50,4 = 3,8.

1. Вихідні і розрахункові дані для побудови економетричної моделі

№ п∕п	хі	уі	хі²	уі²	хіуі	хі - х	уі - у	(хі - х)²	(хі – х) (уі – у)	ŷі	ui	ui²	(уі - y)²	(ŷі – y)²
						-10,8	-4,2	116,64	45,36	48,8	1,2	1,44	17,64	29,16
						-25,8	-14,2	665,64	336,36	41,3	-1,3	1,69	201,64	166,41
						19,2	10,8	368,64	207,36	63,8	1,2	1,44	116,64	92,16
						-0,8	0,8	0,64	-0,64	53,8	1,2	1,44	0,64	0,16
						-20,8	-9,2	432,64	181,36	43,8	1,2	1,44	84,64	108,16
						-22,8	-12,2	519,64	278,16	42,8	-0,8	0,64	148,84	129,96
						9,2	1,8	84,64	16,56	58,8	-2,8	7,84	3,24	21,16
						14,2	5,8	201,64	82,36	61,3	-1,3	1,69	33,64	50,41
						14,2	9,8	201,64	139,16	61,3	2,7	7,29	96,04	50,41
						24,2	10,8	585,64	261,26	66,3	-1,3	1,69	116,64	146,41
∑									1587,5			26,6	819,6	794,4

Оскільки вільний член моделі â₀ ≠ 0 то рівень витрат на одиницю продукції не є строго пропорційним до рівня фондомісткості, â₁ = 0,5 показує, що граничне збільшення витрат при зростанні фондомісткості продукції на 1 ум. од. становить 0,5 ум. од.

Еластичність витрат щодо фондомісткості продукції визначається коефіцієнтом еластичності:

Е = / ;

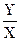Е = 0,5 · 1,8519 = 0,93.

Значення цього коефіцієнта слід тлумачити так: при збільшенні фондомісткості продукції на 1 % витрати на одиницю продукції зростуть на 0,93 %.

Залишки обчислюються згідно з рівністю:

u_i = y_i – ŷ_i.

Оцінка дисперсії залишків подається так:

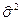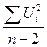= = =3,325.

Для залишків u_i можна задати певну функцію закону розподілу, наприклад функцію нормального розподілу.

Оцінкою коефіцієнта кореляції є вибірковий коефіцієнт кореляції, який можна обчислити за формулою:

r = ;

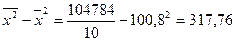= ; = 17,8258;

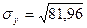= ; =9,0532;

r = = =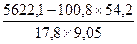0,98.

Вибірковий коефіцієнт кореляції є точковою оцінкою коефіцієнта кореляції і тому потребує перевірки. Вона базується на критерії Стьюдента за формулою:

t= ,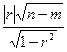

де r −вибірковий коефіцієнт кореляції; n-m− число ступенів вільності.

Якщо t › t_{табл. α}, де t_{табл. α} − відповідне табличне значення t розподілу з (n –m) ступенями вільності, то можна зробити висновок про значущість коефіцієнта кореляції між залежною і незалежною змінними моделі. Для нашого прикладу:

t= 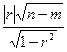= = 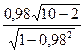=13,9291.

Табличне значення t − критерія для рівня значущості α =0,05 і n−m=8 ступенів вільності дорівнює 2,306. Оскільки t › t_{табл. α} робимо висновок, що коефіцієнт кореляції є значущим і зв’язок між x та y існує.

Для аналізу якості опису існуючої залежності між двома ознаками часто використовують індекс кореляції. Він розраховується за формулою:

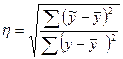= =0,9845≈0,98.

Поиск по сайту: