АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Розв’язання. Запишемо умову ідентифікованості структурних рівнянь:

Читайте также:
  1. Методичні вказівки для розв’язання задач про рівновагу
  2. Органи виконавчої влади, залежно від порядку розв’язання підвідомчих питань, поділяють на єдиноначальні та колегіальні.
  3. Приклад створення та розв’язання системи диференційних рівнянь
  4. Проблема зовнішньої трудової міграції в Україні та шляхи їх розв’язання.
  5. Розв’язання
  6. Розв’язання
  7. Розв’язання
  8. Розв’язання
  9. Розв’язання
  10. Розв’язання
  11. Розв’язання завдань морального виховання відбувається двома основними шляхами:

 

Запишемо умову ідентифікованості структурних рівнянь:

,

де 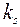— кількість ендогенних змінних, які входять в 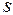-те рівняння;

–– кількість екзогенних змінних, які входять в 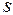-те рівняння;

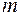— загальна кількість екзогенних змінних.

Для першого рівняння:

;

;

.

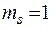Звідси 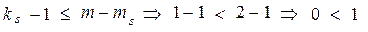, тобто рівняння системи є надідентифікованим.

 

Для другого рівняння:

;

;

.

Звідси тобто друге рівняння системи є точно ідентифікованим.

 

Для третього рівняння:

;

;

.

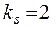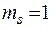Звідси тобто це рівняння системи є також точно ідентифікованим.

Зважаючи на те, що перше рівняння моделі є надідентифікованим, для оцінки його параметрів можна використати метод 2МНК.

Друге та третє рівняння моделі є точно ідентифікованими, тому для оцінки параметрів цих рівнянь можна використати як метод 2МНК, так і НМНК. Обидва методи дають однакові оцінки параметрів моделі.

 

Приклад 9.2. На основі даних, які наведені у табл. 9.1, треба побудувати економетричну модель попиту й пропозиції. Дати аналіз побудованої моделі.

9.1 Вихідні та розрахункові дані для побудови економетричної моделі

Номер спостереження Рівноважна кількість споживання продукту (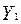) Ціна продукту, млн грн. () Дохід на душу населення, млн грн. (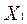) Витрати на виробництво одиниці продукції, млн грн. ()
    0,35   0,10
    0,40   0,15
    0,41   0,16
    0,39   0,12
    0,52   0,18
    0,38   0,12
    0,56   0,20
    0,40   0,16

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)