 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тренд часового ряду та його виявлення
Для моделювання тренду передусім необхідно провести попередній аналіз.
Попередній аналіз часових рядів економічних показників полягає насамперед у перевірці однорідності ряду, тобто у виявленні й усуненні аномальних значень рівнів ряду, а також визначенні повноти даних, можливості їх зіставлення і стійкості.
Під аномальним рівнем розуміють окремі значення рівнів часового ряду, які суттєво впливають на основні часові характеристики ряду динаміки: середній рівень, середній приріст, середній темп зростання, середній темп приросту тощо, а також на відповідну трендову модель. Причинами аномальних спостережень можуть бути помилки технічного характеру, або помилки першого роду, що виникають при агрегуванні або дезагрегуванні показників чи при передаванні інформації та ін. Помилки першого роду мають бути виявлені й усунуті.
Крім того, аномальні рівні в часових рядах можуть виникати через впливи факторів, що мають об'єктивний характер, але можуть діяти рідко, епізодично. Такі помилки мають назву помилки другого роду і не можуть бути усунутими.
Для виявлення аномальних явищ використовується ряд статистичних методів. Наведемо один з них: метод Ірвіна.
Метод Ірвіна припускає використання такої формули:
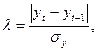
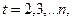 де
де 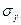 - середнє квадратне відхилення часового ряду,
- середнє квадратне відхилення часового ряду, 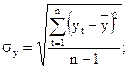
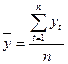 .
.
Розраховані значення 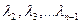 порівнюються з критичним значенням критерію Ірвіна
порівнюються з критичним значенням критерію Ірвіна 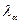 , і, якщо вони будуть більші за таб-
, і, якщо вони будуть більші за таб-
личні, відповідне значення ряду yt вважається аномальним. Рівень значущості α, як правило, береться 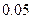
Після виявлення аномальних явищ необхідно з'ясувати причини їх виникнення. Якщо усунути ці причини немає можливості, то їхній рівень, як правило, замінюється середнім значенням ряду або арифметичною середньою двох сусідніх з ними рівнів тощо.
Злами в тенденції ряду говорять про зміну закономірності розвитку процесу або про зміну методики обчислення значень показників. Якщо значення в кінці ряду «випадає» із загальної тенденції, то без додаткової інформації про причини «викиду» на кінці ряду не можна визначити, що це — аномальне спостереження або свідчення зміни тенденції. У такому разі важливо провести якісний аналіз цих змін або дочекатись надходження нового спостереження. Якщо злам тенденції зумовлюється зміною методики розрахунку показника, то рівні ряду, які наводились попереду зламу, можуть бути використані в оцінках характеристик динаміки і для побудови моделі тільки після їх перерахунку за новою методикою. Якщо ж злам тенденції відображає зміну закономірностей розвитку процесу, то за інформаційну базу для статистичного аналізу потрібно взяти рівень останнього зламу тенденції.
Продовжуючи попередній аналіз часового ряду в напрямі виявлення тренду, необхідно провести статистичну перевірку наявності його в динамічному ряду. Для цього розроблено цілу низку методів. Наведемо кілька з них, що найчастіше застосовується.
1. Метод перевірки різниць середніх рівнів. Реалізація цього методу складається з чотирьох етапів.
1-й етап. Початковий часовий ряд 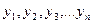 розбивається на дві частини приблизно однієї довжини:
розбивається на дві частини приблизно однієї довжини: 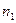 і
і 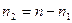
2-й етап. Для кожної частини ряду розраховується середнє значення і дисперсії:
 ;
; 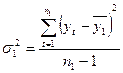 ;
;
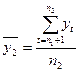 ;
; 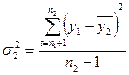 .
.
3-й етап. Перевіряється однорідність дисперсій обох частин за допомогою критерію Фішера Fa:
 якщо
якщо 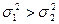 ;
;
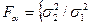 , якщо
, якщо 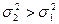
Рівень значущості а беруть таким, що дорівнює 0,1; 0,01 або 0,05. Якщо розраховане значення 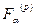 менше за табличне
менше за табличне 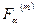 , то гіпотеза про рівність дисперсій приймається і переходимо до четвертого етапу. Якщо
, то гіпотеза про рівність дисперсій приймається і переходимо до четвертого етапу. Якщо 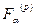 більше або дорівнює
більше або дорівнює 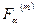 — гіпотеза про рівність дисперсій відхиляється і робиться висновок, що даний метод про визначення наявності тренду відповіді не дає.
— гіпотеза про рівність дисперсій відхиляється і робиться висновок, що даний метод про визначення наявності тренду відповіді не дає.
4-й етап. Перевіряється гіпотеза про відсутність тренду з використанням /-критерію Стьюдента. Для цього визначається розрахункове значення критерію Стьюдента за формулою:
 , (1)
, (1)
де σ— середньоквадратичне відхилення різниці середніх, що визначається так:
 (2).
(2).
Якщо розрахункове значення tp менше або дорівнює табличному значенню 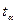 (із рівнем значущості α), то гіпотеза про відсутність тренду приймається у протилежному випадку, тобто коли
(із рівнем значущості α), то гіпотеза про відсутність тренду приймається у протилежному випадку, тобто коли 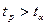 , то з імовірністю 1-α приймається гіпотеза про існування тренду.
, то з імовірністю 1-α приймається гіпотеза про існування тренду.
2. Метод Фостера — Стюарта. Основні показники методу Фостера—Стьюарта такі:
 і
і 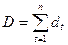 ,
,
де 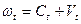 ,
, 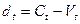 , причому параметри
, причому параметри 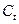 і
і 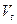 мають наведені далі значення:
мають наведені далі значення:
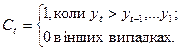
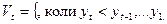 (3).
(3).
З наведених співвідношень випливає, що 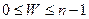 .
.
Якщо всі рівні ряду однакові, тобто  то W= 0.
то W= 0.
Якщо 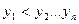 , то
, то 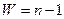 .
.
Аналогічно знаходять: 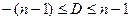
Показники D і W застосовуються для визначення тенденції зміни в часі відповідного середнього значення 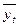 і дисперсії
і дисперсії 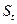 .
.
Після визначення для ряду значень D і W за критерієм Стьюдента перевіряються гіпотези про відсутність тенденції в середньому значенні D і W:
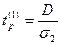 ;
;  , (4),
, (4),
де 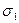 і
і  - середні квадратичні відхилення для W і D,
- середні квадратичні відхилення для W і D,
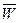 - середнє значення параметра W.
- середнє значення параметра W.
Значення 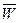 ,
, 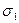 і
і  знаходяться за табл. 11. 1.
знаходяться за табл. 11. 1.
11. 1 Визначення основних показників методу Фостера–Стюарта
| n | 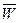
| 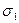
| 
| n | 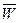
| 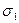
| 
|
| 3,86 | 1,29 | 1,96 | 7,36 | 2,20 | 2,71 | ||
| 3,64 | 1,52 | 2,15 | 7,52 | 2,37 | 2,74 | ||
| 5,19 | 1,68 | 2,28 | 7,67 | 2,67 | 2,77 | ||
| 5,65 | 1,79 | 2,37 | 7,80 | 2,30 | 2,79 | ||
| 5,99 | 1,88 | 2,45 | 7,93 | 2,32 | 2,82 | ||
| 6,29 | 1,96 | 2,51 | 8,05 | 2,35 | 2,84 | ||
| 6,56 | 2,02 | 2,56 | 8,16 | 2,37 | 2,86 | ||
| 6,79 | 2,07 | 2,61 | 8,27 | 2,40 | 2,88 | ||
| 7,00 | 2,12 | 2,64 | 8,37 | 2,42 | 2,89 | ||
| 7,19 | 2,16 | 2,68 | — | — | — | — |
Теоретичне значення t-критерію визначається з табл. 11.1 за 5 %-го рівня значущості. Якщо tp(1) > tтеор і tp(2) > tтеор, то гіпотеза про відсутність тренду з імовірністю 0,95 відхиляється. Якщо ж tp(1) і tp(2) < tтеор, то приймається гіпотеза про відсутність тренду.
Методи визначення тренду.. Метод простої ковзної середньої. Рівні економічних часових рядів коливаються, тому тенденція розвитку економічних явищ у часі явно не може бути визначена через випадкові відхилення рівнів у той чи в інший бік. Щоб якнайчіткіше визначити основну тенденцію ряду (тренд) для подальшого прогнозування процесу, використовуючи ту чи іншу трендову модель, розроблені методи згладжування (вирівнювання) часових рядів, які називають механічним методом визначення тренду.
Отже, статистичні методи згладжування часових рядів поділяють на дві групи: методи механічного методу згладжування ряду та аналітичне вирівнювання, базоване на кривих зростання.
Суть методів механічного згладжування полягає в такому. Береться кілька перших рівнів часового ряду (три, чотири, п'ять чи сім), кількість яких утворює інтервал згладжування. Для них добирається поліном, степінь якого має бути меншим за кількість рівнів, що входять в інтервал згладжування; за допомогою полінома розраховуються нові, вирівняні значення рівнів до середини інтервалу. Далі інтервал згладжування зрушується на один рівень праворуч (або вниз), обчислюється наступне згладжуване значення тощо.
Найпростішим методом механічного згладжування є метод простої ковзної середньої. Спочатку для часового ряду 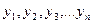 визначається інтервал згладжування т(т < п). Якщо потрібно згладити дрібні безпорадні коливання, то інтервал згладжування беруть за можливістю більшим; інтервал згладжування зменшують, якщо потрібно зберегти дрібніші коливання. За інших однакових умов інтервал згладжування рекомендується брати непарним. Для перших т рівнів часового ряду обчислюється їхнє середнє арифметичне; це буде згладжуване значення рівня ряду, яке відповідає середині інтервалу згладжування. Далі інтервал згладжування зсувається на один рівень праворуч (або вниз), повторюється обчислення середньої арифметичної і т. д. Для обчислення згладжених рівнів ряду yt застосовуємо формулу:
визначається інтервал згладжування т(т < п). Якщо потрібно згладити дрібні безпорадні коливання, то інтервал згладжування беруть за можливістю більшим; інтервал згладжування зменшують, якщо потрібно зберегти дрібніші коливання. За інших однакових умов інтервал згладжування рекомендується брати непарним. Для перших т рівнів часового ряду обчислюється їхнє середнє арифметичне; це буде згладжуване значення рівня ряду, яке відповідає середині інтервалу згладжування. Далі інтервал згладжування зсувається на один рівень праворуч (або вниз), повторюється обчислення середньої арифметичної і т. д. Для обчислення згладжених рівнів ряду yt застосовуємо формулу:

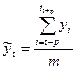 , t > p, (5)
, t > p, (5)
де i – порядковий номер рівня ряду;
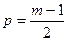 – (для непарних m; для парних m формула ускладнюється).
– (для непарних m; для парних m формула ускладнюється).
Отже, послідовно проводячи такі обчислення, одержимо n-m+1згладжених значень рівнів ряду; згідно з цим перші й останні p рівнів ряду не губляться – це є першим недоліком цього методу.
Другим недоліком є те, що він застосовується лише для рядів, що мають лінійну тенденцію.
Метод експоненціального згладжування. Його особливість полягає в тому, що у процедурі відшукання загладжуваного рівня застосовуються значення тільки попередніх рівнів ряду, які беруться з певною вагою. Вага рівня ряду зменшується залежно від того, на скільки віддалений рівень від моменту часу, для якого визначається згладжуване значення. Вага рівнів знижується експоненціально, що залежить від зазначеної величини параметра згладжування а, значення якого міститься в інтервалі 0 < α < 1.
Якщо для вихідного часового ряду 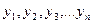 відповідні згладжені значення рівнів ряду позначити через
відповідні згладжені значення рівнів ряду позначити через 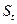 ,t=1,2…n,то експоненціальне згладжування розраховується за формулою:
,t=1,2…n,то експоненціальне згладжування розраховується за формулою:
 (6)
(6)
де α — параметр для згладжування; 1-α має назву коефіцієнта дисконтування.
Використовуючи наведені щойно рекурентні співвідношення для всіх рівнів ряду, починаючи з першого, можна одержати таке співвідношення:
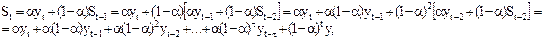
тобто згладжене значення 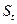 є зваженою середньою всіх попередніх рівнів.
є зваженою середньою всіх попередніх рівнів.
У загальному вигляді маємо:
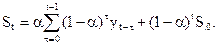 (7)
(7)
У практичних задачах обробки економічних часових рядів рекомендують вибирати параметри згладжування в інтервалі від 0,1 до 0,3. Більш обґрунтованих рекомендацій для α поки що немає.
Зміст
Поиск по сайту: