Тема 8. Моделі розподіленого лага

Для багатьох економічних процесів типовим є те, що ефект від впливу деякого фактора на показник, який характеризує процес, виявляється не одразу, а поступово, через деякий період часу. Таке явище називається лагом.

Потреба враховувати лаг при побудові економетричних моделей постає дуже часто. Наприклад, при визначенні кількісного взаємозв’язку між капітальними вкладеннями і введенням основних фондів, між витратами виробничих ресурсів і обсягом виробництва.

При цьому вплив деяких пояснювальних змінних на залежну може проявлятися не лише через певний період часу, а й протягом певного часу, тобто лаг може складатись з кількох часових періодів.У цьому разі будемо мати справу з економетричною моделлю розподіленого лагу.

Економетричні модель розподіленого лага визначається так:

Y_t = Σa_jx_t-τ + u_t, (8.1)

де a_j − параметри моделі при лагових змінних; x_t-τ − пояснювальна лагова змінна; τ − період зрушення; u_t − залишки, що нормально розподілені.

Модель (8.1) називається загальною моделлю нескінченого розподіленого лага, якщо для неї справджуються такі умови:

1. a_ka_j ≥ 0, для будь-яких k j; (8.2)

2. a_j ≥ 0, j=1,2,3…; k = 1,2,3…; (8.3)

3. , − певне число (8.4)

4. _j = ; (8.5)

5. , 0 ≤ 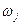≤1. (8.6)

Коефіцієнти a_j, j=0,1,2,3... називаються коефіцієнтами лага, а послідовність a = {a_j, j=0,1,2,3...} − структурою лага.

Якщо економетрична модель включає не тільки лагові змінні, а й змінні, що характеризують поточні умови функціонування економічних систем, то така модель називається узагальненою моделлю розподіленого лага і записується у вигляді:

Y_t = a_τx _t-τ + 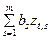+ u_t (8.7).

Труднощі оцінювання параметрів такої моделі пов’язані з необхідністю враховувати обмеження на параметри a_τ. На практиці реалізація такої моделі стикається з труднощами через велику кількість факторів, істотною обмеженістю часових рядів і складністю їх внутрішньої структури.

До економетричних моделей належать такі змінні x _t-τ, для яких лаги обґрунтовані теоретично і перевірені емпірично. Для обґрунтування лага чи лагів доцільно використовувати взаємну кореляційну функцію. Ця функція характеризує тісноту зв’язку кожного елемента вектора залежної змінної Y_t з елементом вектора незалежної змінної х_t, зсунутим один відносно одного на часовий лаг τ.

(8.8).

Для різних значень τ на основі взаємної кореляційної функції можна одержати n+1 значення r_(τ). Значення r_(τ) містяться на множині r_(τ) 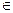]-1,1[. Якщо τ=0, то маємо парний коефіцієнт кореляції. Найбільше значення r_(τ) за модулем (найближче до одиниці) визначає зрушення, або часовий лаг. Якщо серед множини значень r_(τ) є кілька, величини яких наближаються до одиниці, то це означає, що запізнення впливу змінної x_t відбувається протягом певного проміжку часу і в результаті маємо кілька часових лагів для двох взаємопов’язаних часових рядів. Під часовим лагом розуміють зрушення, якому відповідає найбільший коефіцієнт взаємної кореляції. Знайшовши часові лаги для визначення взаємозв’язку між економічними показниками, можна побудувати економетричну модель розподіленого лага. Графік нормованої кореляційної функції називається корелограмою.

Наявність мультиколінеарності між лаговими змінними ускладнює побудову економетричної моделі Щоб позбутися мультиколінеарності необхідно ввести коефіцієнти при лагових змінних. Вони повинні мати однаковий знак і можна знайти їх сумму. Тоді економетрична модель запишеться:

Y_t= (8.9).

Для зображення вагових коефіцієнтів Л. Койк запропонував форму спадної геометричної прогресії, тобто

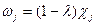, 0≤ ≤1 (8.10).

Тоді економетрична модель запишеться у вигляді

(8.11).

Наявність в економетричній моделі лагової змінної та прийняття гіпотези відносно залишків зумовлюють особливості оцінки параметрів моделі. Це такі гіпотези.

Гіпотеза 1. Залишки є випадковими величинами і розподіляються нормально, тобто .

Гіпотеза 2. Залишки виражені через параметр λ, тобто:

0≤ ≤1;

а) ;

б) .

Гіпотеза 3. Залишки описуються авторегресійною схемою першого порядку:

де , .

Якщо відносно залишків приймається перша гіпотеза, то для оцінки параметрів моделі можна застосувати метод найменших квадратів.

Якщо відносно залишків приймається друга гіпотеза, то застосовується метод Ейткена. В операторі â= (X′V^-1X)^-1X′V^-1Y матриця має вигляд:

1+λ² -λ 0 0 … 0

V= -λ 1+λ² -λ 0 … 0

0 -λ 1+λ² -λ … 0

………………………..

0 0 0 0 … 1+λ²

Коли модель y_t = a₀ +a₁x_t +λy_t-1 +u_t для другої гіпотези можна записати

y_t – λy_t-1 =a₀ +a₂x_t + υ_t (8.12),

та також застосувати метод найменших квадратів для перетворених даних залежної змінної y_t на основі параметра λ. Параметр λ пропонується вибирати довільно на інтервалі 0 <λ<1 так, щоб мінімізувати суму квадратів залишків uV^-1u.

Якщо відносно залишків приймається третя гіпотеза, то для оцінки параметрів моделі можна використовувати:

1) метод найменших квадратів, коли вихідні дані перетворені на основі параметрів λ і ρ;

2) метод Ейткена;

3) ітеративний метод;

4) двокрокову процедуру:

а) метод найменших квадратів для вихідних даних, коли ;

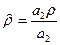б) метод найменших квадратів для перетворених даних на основі ρ = ;

5) метод інструментальних змінних;

6) алгоритм Уолліса.

Щоб застосувати для оцінки параметрів метод найменших квадратів, матриця вихідних даних X(ρ) буде мати вигляд:

λ 1 x₁(ρ)

λ² 1+λ x₂(ρ) + λx₁(ρ)

λ³ 1+λ +λ² x₃ (ρ) +λ x₂(ρ) + λ² x₁(ρ)

. …. …….

λⁿ 1+λ +λ²+…+ λ^n-1 x_n (ρ) + λ x _n-1(ρ) + … +λ^n-1 x ₁(ρ)

Параметри λ і ρ вибираються довільно на множині ]0,1[. Для кожної пари λ і ρ послідовно обчислюються залишки; λ і ρ вибираються доти, поки не буде мінімізована сума відхилень.

Оператор оцінювання методом Ейткена

Â=(X’V^-1X)^-1X^’V^-1Y (8.13)

базується на матриці

1 ρ ρ ² … ρ ^n-1

S = ρ 1 ρ … ρ^n-2

… … … … …

ρ ^n-1 ρ^n-2 ρ ^n-3 … 1,

а матриця Х дорівнює:

1 y₀ x₁

1 y₁ x₂

X = 1 y₂ x₃

… … …

1 y_n-1 x_n

Ітеративний метод є альтернативою методу Ейткена. Його алгоритм має чотири кроки:

Крок 1. Вибирається початкове значення ρ = і підставляється в модель y_t=a₀(1-ρ)+(a₁+ρ)y_t-1-a₁ρy_t-2+a₂x_t-a₂ρx_t-1+ε_t.

Крок 2. Застосовується метод найменших квадратів для оцінки параметрів â₀, â₁, â₂.

Крок 3. У модель (8.13)підставляються параметри â₀, â₁, â₂ і на основі методу найменших квадратів обчислюється параметр .

Крок 4. Задається на основі методу найменших квадратів і розраховуються параметри і тощо.

Метод інструментальних змінних для оцінки параметрів моделі застосовують тоді, коли залишки не автокорельовані, але існує залежність пояснювальних змінних із залишками. Якщо модель має вигляд:

Y_t= a₀ + a₁x_t + a₂x_t-1 + a₃y_t-1 + u_t,

то можна замість змінної y_t-1 використати як інструментальну змінну ŷ_t-1, що розраховується як функція ŷ_t-1 = f(x_t).

Оцінка параметрів моделі з лаговою змінною на основі алгоритму Поліса складається з трьох етапів.

На першому етапі оцінка параметрів моделі виконується на основі методу інструментальних змінних, де x_t-1 використовується як інструментальна змінна для y_t-1 .

На другому етапі обчислюють коефіцієнт автокореляції першого порядку з врахуванням поправки на зміщення і формують матрицю S.

На третьому кроці виконують оцінку параметрів моделі на основі методу Ейткена.

Тема 9. Побудова економетричної моделі на основі системи одночасних структурних рівнянь

Поиск по сайту: