Основні положення теми

Наявність прямих та зворотних зв’язків між економічними показниками в багатьох випадках вимагає використання системи одночасових рівнянь. Вони, як правило, містять лінійні рівняння. Нелінійність зв’язків апроксимується лінійними співвідношеннями. Динаміка економічних зв’язків ураховується за допомогою часових лагів або лагових змінних.

Система одночасових структурних рівнянь у матричній формі має такий вигляд:

.

Якщо кожне рівняння системи розв’язати відносно 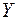, то одержимо приведену форму моделі, яка має вигляд:

,

де залишки є лінійною комбінацією залишків .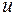

Зв’язок між коефіцієнтами структурної і приведеної форми моделі визначиться:

;

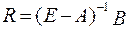або ;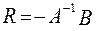

або .

Оцінка параметрів моделі на основі одночасових рівнянь методом 1МНК буде давати зміщення, яке буде дорівнювати:

,

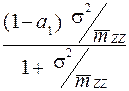де 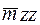— момент другого порядку залежної змінної, який прямує до деякої константи.

Чисельна оцінка параметрів моделі на основі одночасових структурних рівнянь пов’язана з проблемою ідентифікації.

Необхідна умова ідентифікації системи — справедливість нерівності для кожного рівняння:

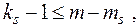
де 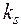— кількість ендогенних змінних, які входять в 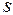-те рівняння структурної форми;

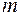— загальна кількість екзогенних змінних моделі;

— кількість екзогенних змінних, які не входять в 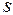-те рівняння структурної форми моделі.

Якщо записане вище співвідношення виконується як рівність, то відповідне рівняння є строгоідентифікованим, а коли — як нерівність, то відповідне рівняння є надідентифікованим.

Якщо в структурній формі моделі 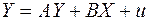матриця є трикутною, а залишки характеризуються діагональною матрицею виду:

,

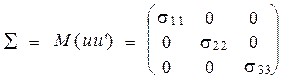то така система рівнянь називається рекурсивною і для оцінки параметрів такої моделі можна застосувати 1МНК.

Якщо кожне рівняння моделі є строгоідентифікованим, то для оцінки параметрів моделі можна застосувати непрямий метод найменших квадратів (НМНК). Алгоритм цього методу складається з чотирьох кроків:

Крок 1. Перевіряється умова ідентифікованості для кожного рівняння. Якщо кожне рівняння точноідентифіковане, то виконується перехід до кроку 2.

Крок 2. Перехід від структурної форми моделі до приведеної.

Крок 3. Оцінка параметрів кожного рівняння приведеної форми моделі 1МНК.

Крок 4. Розрахунок оцінок параметрів рівнянь структурної форми на основі співвідношення:

,

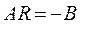де і 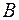— параметри структурних рівнянь, а 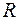— матриця оцінок параметрів приведеної форми моделі.

Якщо рівняння структурної форми моделі надідентифіковані, то для оцінки параметрів моделі застосовується двокроковий метод найменших квадратів (2МНК). Система рівнянь для обчислення оцінок двокроковим методом найменших квадратів запишеться так:

де 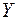— вектор залежної або ендогенної змінної;

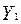— матриця поточних ендогенних змінних, які входять у праву частину рівняння;

Х — матриця всіх пояснювальних або екзогенних змінних;

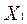— матриця пояснювальних або екзогенних змінних даного рівняння;

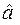— вектор структурних параметрів, які належать до змінних матриці ;

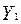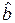— вектор структурних параметрів, які належать до змінних матриці .

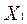Oператор оцінювання 2МНК:

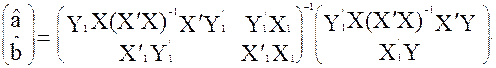
Дисперсія залишків для кожного рівняння:

.

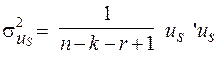Матриця коваріацій параметрів кожного рівняння визначається на основі співвідношення:

Трикроковий метод найменших квадратів (3МНК), на відміну від попередніх, призначений для одночасної оцінки параметрів всіх рівнянь моделі. Оператор оцінювання 3МНК матиме вигляд:

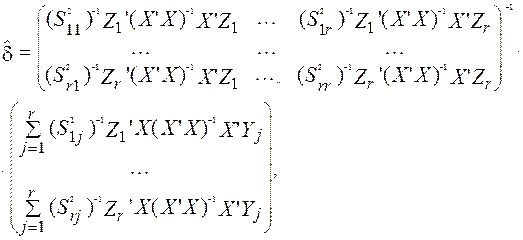
де 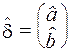— оцінки параметрів моделі;

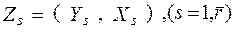, де 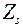— змінні моделі, які знахо­дяться у правій частині 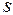-го рівняння;

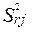— дисперсії залишків для кожного рівняння, які є наближеною оцінкою .

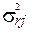Щоб застосувати 3МНК на практиці, необхідно дотримання таких вимог:

1) приступаючи до оцінки параметрів моделі, необхідно виключити всі тотожності;

2) виключити із системи кожне неідентифіковане рівняння;

3) за наявності серед рівнянь системи точноідентифікованих та надідентифікованих, 3МНК доцільно застосувати до кожної з груп рівнянь окремо;

4) якщо група надідентифікованих рівнянь має тільки одне рівняння, то 3МНК перетворюється в 2МНК.

Якщо матриця коваріацій для структурних залишків є блочно-діагональною, то вся процедура оцінювання на основі 3МНК може бути застосована окремо для кожної групи рівнянь, які відповідають одному блоку.

Точковий прогноз залежних змінних визначається на основі приведеної форми економетричної моделі:

,

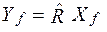де 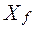— вектор прогнозних екзогенних змінних.

Визначення довірчих інтервалів для цього прогнозу залежить від методу, за допомогою якого була одержана матриця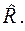

Довірчі інтервали для кожної ендогенної змінної задаються сіввідношенням:

,

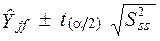де 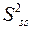— дисперсія залишків 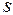- го рівняння моделі;

.

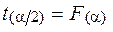Довірчі інтервали для всіх ендогенних змінних визначаються так:

,

де 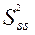— незміщена дисперсія залишків всіх рівнянь моделі.

Ці інтервали будуть ширшими, ніж у випадку, коли їх задавати для кожної ендогенної змінної окремо.

9.2. Економетрична модель на основі системи рівнянь:

Поиск по сайту: