Тема 11. Економетричні моделі динаміки

Показники багатьох явищ і процесів в економіці змінюються в часі. Цей розвиток має назву економічної динаміки. Характер­ним для економічної динаміки є те, що рівень показників у на­ступному часовому періоді значною мірою залежить від їхнього рівня в минулому. Крім того, чим довший часовий інтервал між двома явищами, тим суттєвіша різниця як у кількісному, так і в якісному їхньому стані.

Початковою інформацією математико-статистичного вивчен­ня процесу в розвитку є ряд числових даних, що являє собою зміни деякого економічного показника в часі, який має назву одновимірного ряду.

Отже, дамо визначення одновимірного ряду динаміки.

Послідовність спостережень одного показника (ознаки), упорядкована залежно від послідовно зростаючих або спадних значень другого показника (ознаки) є одновимірним рядом ди­наміки.

Якщо ознакою, за якою відбувається впорядкування ряду, є час, то такий динамічний ряд має назву часового ряду.

Упорядкування економічних показників найчастіше відбува­ється саме за часом, тому в цьому розділі розглянемо принципово нові методи аналізу динамічних рядів на відміну від розділу, де розглядалися сукупності, що утворюють випадкову вибірку.

Одним з основних завдань аналізу рядів у соціально-економічних системах є вивчення структури і класифікації основ­них факторів, під впливом яких формуються складові елементи часового ряду, та його розкладання на ці складові.

Динаміка рядів економічних явищ і процесів у загальному випадку формується під впливом чотирьох груп факторів. До них належать:

· довготривалі, що формують загальну тенденцію. Кожен із цих факторів окремо може діяти на процес, що досліджується, у протилежному напрямі один щодо одного. Проте в сукупності вони формують зростаючу чи спадну тенденцію цього процесу, описувану невипадковою функцією , яку називають функцією тренду, або просто – трендом;

· сезонні, що формують періодичну повторювані за певний час року коливання того чи іншого показника. Це теж є не випадкова функція ;

· циклічні, що формують зміни динаміки ряду, зумовлені дією тривалих циклів економічної, демографічної природи. Результат дії циклічних факторів позначимо за допомогою не випадкової функції ;

· випадкові, які не піддаються реєстрацій й обліку. Їхня дія на формування рівнів часового ряду саме і зумовлює їхню стохастичність. Позначимо цю випадкову функцію

Отже, в найзагальнішому випадку часовий ряд 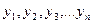економічної динаміки можна розкласти на чотири структурних елементи:

* тренд ;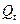

• сезонний компонент ;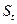

• циклічну складову ;

* випадкову складову .

Таким чином, під трендом розумітимемо стійку систематич­ну зміну процесу протягом довготривалого періоду, тобто тренд визначає зміни, які зумовлюються тривалими постійно діючими факторами, що визначають основну тенденцію часових рядів.

Іноді під трендом розуміють лише зміну показника в серед­ньому за весь період спостереження. Говорять, що тренд відсутній, якщо такої зміни (зростання чи спадання) у середньому немає.

У зв'язку з цим економіко-математична динамічна модель, де розвиток економічної системи моделюється через тренд, має на­зву трендової моделі.

У наведених раніше прикладах показано, що в часових рядах економічних процесів можуть відбуватися також більш або менш регулярні коливання. Якщо вони мають строго періодичний або близький до нього характер і завершуються протягом одного ча­сового періоду, то вони мають назву сезонних коливань.

У тих випадках, коли період коливання становить кілька часо­вих періодів (наприклад, років), говорять, що в часовому ряді є довготривалий циклічний компонент. Тренд, сезонний і циклі­чний компоненти мають назву регулярних, або систематичних компонентів часового ряду. Складову часового ряду, що залиша­ється після вилучення з нього регулярних компонентів, раніше названо випадковою, або нерегулярною.

Вона є обов'язковою складовою часового ряду в економіці, бо випадкові фактори неминуче притаманні будь-якому економіч­ному явищу.

Якщо систематичні регулярні компоненти часового ряду ви­значені правильно, то після їх вилучення залишковий компонент має бути випадковим компонентом часового ряду, тобто повинен мати такі властивості:

• характеризуватись випадковістю коливань рівнів залишкової послідовності (або простіше — залишків);

• відповідністю розподілу ймовірностей рівнів випадкового компонента нормальному закону розподілу;

• рівністю нулю математичного сподівання;

• незалежністю значень рівнів залишків, тобто відсутністю суттєвої між ними автокореляції.

Перевірка адекватності трендових моделей ґрунтується саме на перевірці виконання в залишках наведених вище чотирьох властивостей.

Якщо не виконується хоча б одна з них, модель визначається як неадекватна; навпаки, у разі виконання всіх чотирьох власти­востей — модель є адекватною. Ця перевірка відбувається з ви­користанням певних статистичних критеріїв, які докладніше буде розглянуто далі.

У більшості випадків фактичний рівень часового ряду наво­диться як сума або добуток трендового, сезонного, циклічного й випадкового компонентів:

або

Модель, де часовий ряд наводиться як сума перелічених ком­понентів, має назву адитивної моделі. Модель, де часовий ряд подається через добуток складових компонентів, тобто має назву мультиплікативної моделі.

У цьому розділі розглядатимемо адитивні моделі, які найчас­тіше трапляються у практичному застосуванні.

Отже, виходячи з адитивної природи динамічних рядів, сфор­мулюємо основні цілі їх аналізу:

• визначити, які з наведених щойно складових фор­мують рівні ряду ;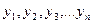

• розрахувати кількісні оцінки параметрів для тих регулярних функцій що є складовими ряду ;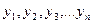

• перевірити адекватне поводження нерегулярної функції ;

• розрахувати ефективну прогнозну модель, виходячи з базо­вого періоду часового ряду .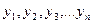

Поиск по сайту: