 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
С распределенным лагом
|
Читайте также: |
Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:
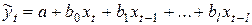 .
.
Данная модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной x, то это изменение будет влиять на значения переменной y в течение l следующих моментов времени.
Коэффициент регрессии 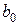 при перемеренной
при перемеренной 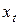 характеризует среднее абсолютное изменение
характеризует среднее абсолютное изменение 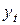 при изменении
при изменении 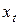 на 1 единицу своего измерения в некоторый фиксированный момент времени
на 1 единицу своего измерения в некоторый фиксированный момент времени  , без учета воздействия лаговых значений фактора
, без учета воздействия лаговых значений фактора 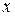 . Этот коэффициент называют краткосрочным мультипликатором.
. Этот коэффициент называют краткосрочным мультипликатором.
В момент 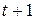 совокупное воздействие факторной переменной
совокупное воздействие факторной переменной 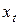 на результат
на результат 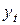 составит
составит 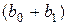 условных единиц, в момент
условных единиц, в момент 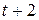 это воздействие можно охарактеризовать суммой
это воздействие можно охарактеризовать суммой 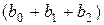 и т. д. Полученные таким образом суммы называют промежуточным мультипликаторами.
и т. д. Полученные таким образом суммы называют промежуточным мультипликаторами.
С учетом конечной величины лага можно сказать, что изменение переменной 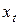 в момент
в момент  на 1 у.е. приведет к общему изменению результата через
на 1 у.е. приведет к общему изменению результата через 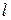 моментов времени на
моментов времени на  абсолютных единиц.
абсолютных единиц.
Введем следующее обозначение:
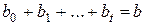
Величину 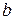 называют долгосрочным мультипликатором, который показывает абсолютное изменение в долгосрочном периоде
называют долгосрочным мультипликатором, который показывает абсолютное изменение в долгосрочном периоде 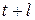 результата
результата 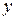 под влиянием изменения на 1 ед. фактора
под влиянием изменения на 1 ед. фактора 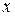 .
.
Предположим, 
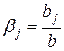 .
.
Назовем полученные величины относительными коэффициентами модели с распределенным лагом. Если все коэффициенты 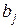 имеют одинаковые знаки, то выполняются условия
имеют одинаковые знаки, то выполняются условия 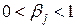 и
и 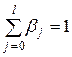 . Каждый из коэффициентов
. Каждый из коэффициентов 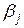 измеряет долю от общего изменения результативного признака в момент времени
измеряет долю от общего изменения результативного признака в момент времени  .
.
Зная величины 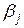 , можно определить еще две важные характеристики: величину среднего и медианного лагов.
, можно определить еще две важные характеристики: величину среднего и медианного лагов.
Средний лаг вычисляется по формуле
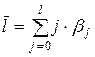
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.
Медианный лаг – это величина лага, для которого 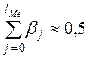 . Это период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.
. Это период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.
Лаги, структуру которых можно описать с помощью полиномов, называют лагами Алмон.
Формально модель зависимости коэффициентов 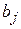 от величины лага j в форме полинома можно записать так:
от величины лага j в форме полинома можно записать так:
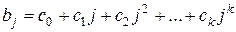 .
.
Тогда каждый из коэффициентов 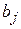 модели
модели 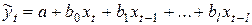 можно выразить следующим образом:
можно выразить следующим образом:
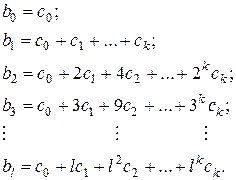 (*)
(*)
Подставив данные соотношения в модель, и перегруппировав слагаемые, получим
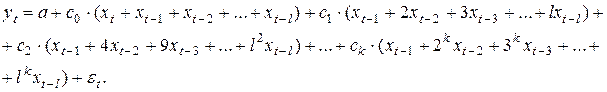
Введем новые обозначения
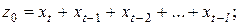
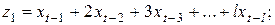
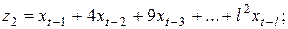
……………………………………………..
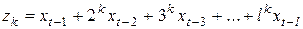 .
.
Тогда модель с распределенным лагом будет выглядеть следующим образом:
 .
.
Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выполняется следующим образом:
1. Определяется максимальная величина лага l.
2. Определяется степень полинома k, описывающего структуру лага.
3. Рассчитываются значения переменных 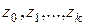 .
.
4. Определяются параметры уравнения линейной регрессии  по данным значениям
по данным значениям 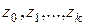 и
и 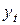 .
.
5. С помощью соотношений (*) рассчитываются параметры 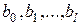 исходной модели с распределенным лагом
исходной модели с распределенным лагом  .
.
Пример.
В таблице представлены данные по региону о месячном доходе на душу населения (x) и денежных расходах населения (y) по месяцам за 2 года.
| y | ||||||||||||
| x | ||||||||||||
| y | ||||||||||||
| x |
Задание.
I. Построить модель с распределенным лагом используя лаги от одного до трех месяцев
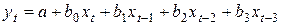
При этом необходимо:
1. Применить обычный МНК.
2. Применить метод Алмон, исходя из предположения, что лаг имеет линейную структуру 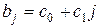 .
.
3. Рассчитать средний и медианный лаги.
II. Построить модель с распределенным лагом используя лаги от одного до четырех месяцев
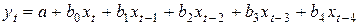 .
.
При этом необходимо:
1. Применить обычный МНК.
2. Применить метод Алмон, исходя из предположения, что структура лага описывается полиномом второй степени 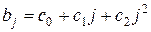 , где
, где 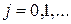
3. Рассчитать средний и медианный лаги.
I. Выполняем расчет для регрессии 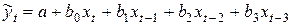 через Анализ данных/Регрессия. Для этого строим вспомогательную таблицу
через Анализ данных/Регрессия. Для этого строим вспомогательную таблицу
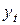
| 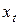
| 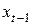
| 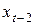
| 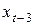
|
Протокол расчета:
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,997244635 | ||||
| R-квадрат | 0,994496863 | ||||
| Нормированный R-квадрат | 0,993121078 | ||||
| Стандартная ошибка | 5,802269075 | ||||
| Наблюдения | |||||
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 97343,91021 | 24335,97755 | 722,85812 | 7,53348E-18 | |
| Остаток | 538,6612227 | 33,66632642 | |||
| Итого | 97882,57143 | ||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | ||
| Y-пересечение | -8,212350419 | 4,986282848 | -1,646988482 | 0,1190561 | |
| Переменная X 1 | 0,618169232 | 0,149223144 | 4,142582811 | 0,0007651 | |
| Переменная X 2 | -0,056537753 | 0,206740199 | -0,273472472 | 0,787987 | |
| Переменная X 3 | 0,323694928 | 0,20619296 | 1,569864111 | 0,136009 | |
| Переменная X 4 | 0,066599661 | 0,154758466 | 0,430345831 | 0,672684 |
То есть модель имеет вид
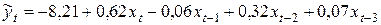 .
.
Удовлетворительным результат назвать нельзя, поскольку
· вычисленные коэффициенты не являются статистически значимыми (вероятность ошибки их расчета значительно превышают допустимый уровень в 0,05);
· коэффициенты имеют разные знаки, что противоречит здравому смыслу: влияние признака x в разные периоды не может быть разнонаправленным.
2) Применяем метод Алмон для расчета параметров модели
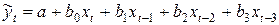 .
.
а) Структура лага линейная, т.е. 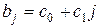
Необходимо преобразовать исходные данные в новые переменные 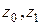 . Это преобразование выглядит следующим образом:
. Это преобразование выглядит следующим образом:
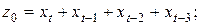
 .
.
| y | x | ||
| z0 | z1 | ||
Строим регрессию 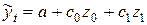
Протокол расчета
| Регрессионная статистика | |||||
| Множественный R | 0,99673 | ||||
| R-квадрат | 0,993471 | ||||
| Нормированный R-квадрат | 0,992745 | ||||
| Стандартная ошибка | 5,958766 | ||||
| Наблюдения | |||||
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 97243,44739 | 48621,72369 | 1369,360199 | 2,15734E-20 | |
| Остаток | 639,1240428 | 35,50689127 | |||
| Итого | 97882,57143 | ||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | ||
| а | -7,81343 | 5,112546309 | -1,528284687 | 0,143824277 | |
| с0 | 0,413363 | 0,083158004 | 4,970810164 | 9,88999E-05 | |
| с1 | -0,11675 | 0,056121391 | -2,080299087 | 0,052057898 |
По найденным коэффициентам 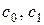 находим параметры
находим параметры 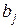 , а именно
, а именно
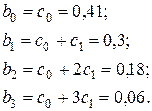
Получили модель с распределенным лагом
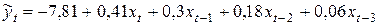 .
.
Эта регрессия лишена недостатков предыдущей:
· вычисленные коэффициенты являются статистически значимыми (вероятность ошибки их расчета почти не превышают допустимый уровень в 0,05);
· коэффициенты имеют одинаковые знаки.
Сравним исходные данные и результаты регрессии:
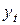
| 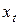
| 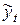
| 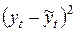
| 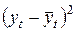
| |
| 116,1747 | 1,380007 | 12736,73469 | |||
| 127,7237 | 39,39197 | 8809,163265 | |||
| 138,3324 | 40,09969 | 9188,591837 | |||
| 148,9222 | 15,38369 | 6865,306122 | |||
| 156,4765 | 0,22705 | 5163,44898 | |||
| 164,28 | 7,398396 | 3703,591837 | |||
| 174,8603 | 9,857755 | 2485,734694 | |||
| 192,9347 | 82,17878 | 668,5918367 | |||
| 214,4897 | 0,239842 | 192,0204082 | |||
| 223,8711 | 1,274391 | 8,163265306 | |||
| 234,7261 | 5,170752 | 83,59183673 | |||
| 245,7482 | 22,5451 | 172,7346939 | |||
| 257,1173 | 172,0626 | 260,5918367 | |||
| 266,5144 | 110,5516 | 792,0204082 | |||
| 273,223 | 4,941541 | 1861,306122 | |||
| 278,5463 | 89,37272 | 3617,163265 | |||
| 285,8544 | 9,895109 | 3738,44898 | |||
| 296,9458 | 0,002938 | 4780,734694 | |||
| 310,1861 | 3,290132 | 7080,020408 | |||
| 330,1949 | 23,08866 | 11479,59184 | |||
| 347,8782 | 0,771296 | 14195,02041 | |||
| Среднее | 227,8571 | ||||
| Сумма | 639,124 | 97882,57143 |
Для оценки качества построения модели сравниваем остаточную и общую дисперсии. Отношение суммы квадратов остатков регрессии к общей сумме квадратов отклонений уровней ряда от его среднего значения равно
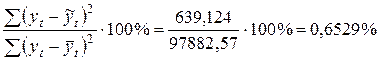 .
.
Построенная модель достоверна на больше, чем на 99%.
Рассчитаем средний и медианный лаг по построенной модели временного ряда. Для удобства данные сводим в таблицу
| Лаг, j | Коэффициенты модели 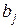
| Относительные коэффициенты
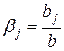 , ,
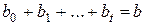
| Средний лаг
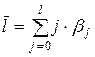
| Медианный лаг –величина лага, для которого 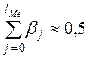 . .
|
| 0,41 | 0,43 | 
| 
| |
| 0,3 | 0,31 | |||
| 0,18 | 0,19 | |||
| 0,06 | 0,07 | |||
| Выводы: Такая величина среднего и медианного лагов свидетельствует об относительно быстром реагировании результата на изменение фактора, в основном в текущем и следующем за текущим периоде. |
II. Строим модель с распределенным лагом в четыре временных периода, исходя из гипотезы о квадратичной структуре лага 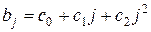 .
.
Тогда
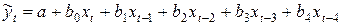 .
.
Преобразование для вспомогательных переменных выглядит следующим образом:
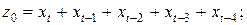
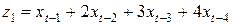 ;
;
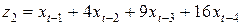 .
.
Строим регрессию 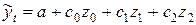 .
.
| y | x | |||
| z0 | z1 | z2 | ||
Протокол расчета
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,996328351 | ||||
| R-квадрат | 0,992670183 | ||||
| Нормированный R-квадрат | 0,991295843 | ||||
| Стандартная ошибка | 6,222115169 | ||||
| Наблюдения | |||||
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 83889,56453 | 27963,18818 | 722,28832 | 2,77251E-17 | |
| Остаток | 619,4354747 | 38,71471717 | |||
| Итого | |||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | ||
| a | -6,683191872 | 6,247481362 | -1,069741786 | 0,3006088 | |
| с0 | 0,457847985 | 0,116502829 | 3,929930209 | 0,0011959 | |
| с1 | -0,239601907 | 0,191844893 | -1,248935549 | 0,2296532 | |
| с2 | 0,035280787 | 0,047693437 | 0,739740933 | 0,4701727 |
По найденным коэффициентам 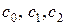 находим параметры
находим параметры 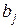 , а именно
, а именно
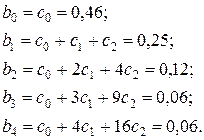
Получили модель с распределенным лагом в четыре периода:
 .
.
Сравним исходные данные и результаты регрессии:
| 
| 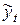
| 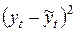
| 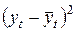
| |
| 128,6768 | 28,33637171 | 8809,163265 | |||
| 138,3068 | 39,77582876 | 9188,591837 | |||
| 148,7868 | 14,3399158 | 6865,306122 | |||
| 155,7168 | 0,080197636 | 5163,44898 | |||
| 164,2568 | 7,525101647 | 3703,591837 | |||
| 175,2768 | 7,415773972 | 2485,734694 | |||
| 194,0068 | 63,8911163 | 668,5918367 | |||
| 214,6868 | 0,471705405 | 192,0204082 | |||
| 221,4068 | 12,91102783 | 8,163265306 | |||
| 232,8968 | 16,83618354 | 83,59183673 | |||
| 245,8768 | 23,78325752 | 172,7346939 | |||
| 257,4968 | 182,1638296 | 260,5918367 | |||
| 265,2268 | 85,13398823 | 792,0204082 | |||
| 272,2668 | 1,604802833 | 1861,306122 | |||
| 278,0368 | 99,26519228 | 3617,163265 | |||
| 285,9668 | 9,200252932 | 3738,44898 | |||
| 297,3368 | 0,113439715 | 4780,734694 | |||
| 310,1568 | 3,397356277 | 7080,020408 | |||
| 330,1268 | 23,74799902 | 11479,59184 | |||
| 346,7768 | 0,049814612 | 14195,02041 | |||
| Среднее | 227,8571 | ||||
| Сумма | 620,0431557 | 85145,83673 |
Для оценки качества построения модели сравниваем остаточную и общую дисперсии. Отношение суммы квадратов остатков регрессии к общей сумме квадратов отклонений уровней ряда от его среднего значения равно
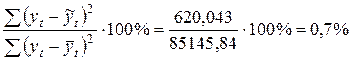 .
.
Построенная модель также как и предыдущая достоверна больше, чем на 99%.
Задание для самостоятельной работы
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | |||||
| x | y | y | x | y | x | x | y | x | y |
| 3,5 | 1,51 | 70,8 | 101,7 | ||||||
| 6,5 | 3,6 | 1,5 | 98,7 | 101,1 | 101,6 | 76,8 | 6,5 | ||
| 6,8 | 3,7 | 1,53 | 97,9 | 100,4 | 107,2 | 79,9 | 6,8 | ||
| 3,7 | 1,53 | 99,6 | 100,1 | 111,1 | 80,5 | ||||
| 7,4 | 3,8 | 1,55 | 96,1 | 115,1 | 71,3 | 7,4 | |||
| 3,9 | 1,58 | 103,4 | 100,1 | 120,9 | 115,4 | ||||
| 8,2 | 4,1 | 1,62 | 95,5 | 127,4 | 150,8 | 8,2 | |||
| 8,7 | 4,2 | 1,65 | 102,9 | 105,8 | 134,4 | 8,7 | |||
| 4,3 | 1,63 | 77,6 | 138,8 | 174,6 | |||||
| 4,4 | 1,65 | 102,3 | 99,8 | 143,7 | 264,4 | ||||
| 10,5 | 4,5 | 1,67 | 102,9 | 102,7 | 328,8 | 10,5 | |||
| 4,5 | 1,64 | 123,1 | 109,4 | 294,33 | |||||
| 4,6 | 1,69 | 74,3 | 116,84 | ||||||
| 12,8 | 4,7 | 1,74 | 92,9 | 106,4 | 94,22 | 12,8 | |||
| 4,9 | 1,8 | 103,2 | 44,18 | ||||||
| 4,8 | 1,75 | 99,8 | 103,2 | 59,82 | |||||
| 4,8 | 1,65 | 105,2 | 102,9 | 48,67 | |||||
| 1,73 | 99,7 | 100,8 | 28,45 | ||||||
| 5,1 | 1,81 | 99,7 | 101,6 | 20,28 | |||||
| 23,1 | 5,3 | 1,87 | 107,9 | 101,5 | 17,9 | 23,1 | |||
| 5,4 | 1,88 | 98,8 | 101,4 | 18,5 | |||||
| 5,4 | 1,8 | 104,6 | 101,7 | 46,81 | 16,89 | ||||
| 5,4 | 1,84 | 106,4 | 101,7 | 43,25 | 10,89 | ||||
| 122,7 | 101,2 |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 | |||||
| y | x | x | y | y | x | y | x | x | y |
| 98,7 | 101,1 | 70,8 | 101,7 | 3,5 | 1,51 | 6,8 | |||
| 97,9 | 100,4 | 98,7 | 101,1 | 3,6 | 1,5 | ||||
| 99,6 | 100,1 | 97,9 | 100,4 | 3,7 | 1,53 | 7,4 | |||
| 96,1 | 99,6 | 100,1 | 3,7 | 1,53 | |||||
| 103,4 | 100,1 | 96,1 | 3,8 | 1,55 | 8,2 | ||||
| 95,5 | 103,4 | 100,1 | 3,9 | 1,58 | 8,7 | ||||
| 102,9 | 105,8 | 95,5 | 4,1 | 1,62 | |||||
| 77,6 | 102,9 | 105,8 | 4,2 | 1,65 | |||||
| 102,3 | 99,8 | 77,6 | 4,3 | 1,63 | 10,5 | ||||
| 102,9 | 102,7 | 102,3 | 99,8 | 4,4 | 1,65 | ||||
| 123,1 | 109,4 | 102,9 | 102,7 | 4,5 | 1,67 | ||||
| 74,3 | 123,1 | 109,4 | 4,5 | 1,64 | 12,8 | ||||
| 92,9 | 106,4 | 74,3 | 4,6 | 1,69 | |||||
| 103,2 | 92,9 | 106,4 | 4,7 | 1,74 | |||||
| 99,8 | 103,2 | 103,2 | 4,9 | 1,8 | |||||
| 105,2 | 102,9 | 99,8 | 103,2 | 4,8 | 1,75 | ||||
| 99,7 | 100,8 | 105,2 | 102,9 | 4,8 | 1,65 | ||||
| 99,7 | 101,6 | 99,7 | 100,8 | 1,73 | 23,1 | ||||
| 107,9 | 101,5 | 99,7 | 101,6 | 5,1 | 1,81 | ||||
| 98,8 | 101,4 | 107,9 | 101,5 | 5,3 | 1,87 | ||||
| 98,8 | 101,4 | 5,4 | 1,88 | ||||||
Лабораторная работа №10
Поиск по сайту: