По особенностям остаточных величин

Практические рекомендации по выполнению расчетов

с помощью табличного редактора MS Excel

Представлены данные о доходах по акциям x и балансовой прибыли y по 11 предприятиям одной отрасли, ден. ед.

Необходимо:

Проверить выполнение следующих требований:

1. Уровни 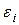ряда остатков имеют случайный характер.

2. Математическое ожидание уровней ряда остатков равно нулю.

3. Значения 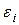независимы друг от друга, т.е. отсутствует автокорреляция.

1. Для проверки случайности ряда остатков можно использовать критерий поворотных точек (пиков). Предварительно составляют таблицу данных:

		…
		…

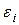
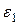
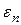
Точка 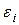считается поворотной, если выполняются следующие условия

или 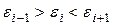. (5.1)

Далее подсчитывается число поворотных точек p. Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение равенства

, (5.2)

где – целая часть числа. Если неравенство выполняется, то модель считается адекватной.

Пусть расчет регрессии дал следующие результаты

,

	x	y		Остатки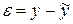
			9,165277	2,834723
			12,39552	0,604484
			15,62576	4,374245
			22,08623	-3,086233
			25,31647	5,683528
			31,77695	-7,77695
			35,00719	5,992811
			38,23743	-10,237428
			47,92815	4,071855
			64,07934	-9,07934
			96,38173	6,61827
Среднее				-3,18182E-06

Жирным шрифтом выделены поворотные точки. Их всего 9, в этом легко убедиться, если просмотреть пики графика (значения фактора x должны быть отсортированы по возрастанию).

.

Неравенство верное, остатки признаем случайными.

2. Для проверки равенства математического ожидания остаточной последовательности нулю вычисляется среднее значение ряда остатков

.

Если , то считается, что модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего. Если , то проверяется гипотеза о равенстве нулю математического ожидания. Для этого вычисляют t -критерий Стъюдента по формуле

,

где – среднее квадратическое отклонение ряда остатков, , m – число параметров при переменной x.

Значение t -критерия сравнивают с критическим при заданном уровне значимости. Если выполняется неравенство , то модель неадекватна по данному критерию.

По расчетам 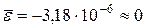, то есть по данному пункту модель признаем адекватной.

3. Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществляют с помощью d -критерия Дарбина-Уотсона. Расчетное значение критерия определяется по формуле

(5.6)

и сравнивается с нижним и верхним 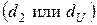критическими значениями статистики Дарбина-Уотсона.

Возможны следующие случаи:

1) Если 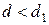, то гипотеза о независимости остатков отвергается, и модель признается неадекватной по критерию независимости остатков.

2) Если , включая сами эти значения, то считается, что нет достаточных оснований делать тот или иной вывод.

3) Если 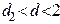, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию.

4) Если , то это свидетельствует об отрицательной автокорреляции остатков. В этом случае расчетное значение критерия необходимо преобразовать по формуле и сравнивать с критическим значением не d, а .

Составляем вспомогательную таблицу:

	x	y		Остатки ε
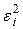
			9,165277	2,834723		8,035654
			12,39552	0,604484	4,973965997	0,365400906
			15,62576	4,374245	14,211098	19,13401932
			22,08623	-3,086233	55,65873199	9,52483413
			25,31647	5,683528	76,908708	32,30249053
			31,77695	-7,77695	181,184468	60,4809513
			35,00719	5,992811	189,606318	35,91378368
			38,23743	-10,237428	263,420658	104,8049321
			47,92815	4,071855	204,75558	16,58000314
			64,07934	-9,07934	172,9539299	82,43441484
			96,38173	6,61827	246,4149597	43,80149779
Сумма					1410,088418	413,3779817

Определяем значение 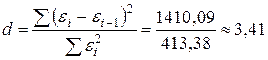. Критические значения критерия Дарбина-Уотсона находят по специальным таблицам для заданных объема наблюдений n и числа независимых переменных модели (см. приложение).

В нашем случае 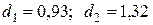. Имеем отрицательную автокорреляцию остатков. Переходим к , .

Так как , модель признается неадекватной, остатки регрессии взаимозависимы. Уравнение регрессии не может быть использовано для прогнозирования. Автокорреляция в остатках может иметь разные причины. Возможно, форма связи неточна, или в уравнение не включен какой-либо существенный фактор.

Задание для самостоятельной работы

1. Провести проверку адекватности линейной регрессии, построенной в лабораторной работе №1

2. Провести проверку адекватности множественной регрессии, построенной в лабораторной работе №3

Поиск по сайту: