Проблема идентификации

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формой модели. В зависимости от условий определения структурных коэффициентов модели по приведенным коэффициентам любая структурная модель может быть отнесена к одному из трех классов: идентифицируемая, неидентифицируемая и сверхидентифицируемая.

Модель идентифицируема, если все структурные коэффициенты однозначно определяются через приведенные коэффициенты.

Модель неидентифицируема, если структурные коэффициенты невозможно найти по приведенным коэффициентам.

Модель сверхидентифицируема, если структурные коэффициенты, выраженные через приведенные коэффициенты, имеют два и более числовых значений.

В идентифицируемой модели количество структурных и приведенных коэффициентов одинаково. Если структурных коэффициентов больше (меньше), чем приведенных, то модель соответственно неидентифицируема (сверх идентифицируема).

Проверка структурной модели на идентифицируемость позволяет установить степень возможности оценивания коэффициентов структурных уравнений по коэффициентам приведенных уравнений.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Рассмотрим необходимое условие идентификации.

Если обозначить число эндогенных переменных уравнения через H, а число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение, – через D, то необходимое условие идентифицируемости модели может быть записано в виде следующего счетного правила:

– уравнение идентифицируемо;

– уравнение неидентифицируемо;

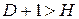– уравнение сверхидентифицируемо.

Предположим, рассматривается следующая система одновременных уравнений:

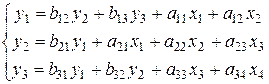
1) Для 1-го уравнения 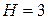, 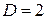. Уравнение идентифицируемо.

2) Для 2-го уравнения 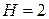, . Уравнение идентифицируемо.

3) Для 3-го уравнения 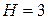, 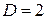. Уравнение идентифицируемо.

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Более точным (достаточным) условием идентификации является следующее:

Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем в число эндогенных переменных в системе без одного.

Для решения идентифицируемых уравнений применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных - двухшаговый метод наименьших квадратов.

Косвенный МНК состоит в следующем:

1) составляют приведенную форму модели и определяют численные значения параметров для каждого ее уравнения в отдельности с помощью обычного МНК;

2) путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.

Двухшаговый МНК заключается в следующем:

1) составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения в отдельности с помощью обычного МНК;

2) выявляют эндогенные переменные, находящиеся в правой части структурного уравнения (параметры которого определяют двухшаговым МНК) и находят расчетные значения по полученным на первом этапе соответствующим уравнениям приведенной формы модели;

3) с помощью обычного МНК определяют параметры каждого структурного уравнения в отдельности, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения, полученные на втором этапе.

Пример1.

Рассмотрим следующую структурную модель:

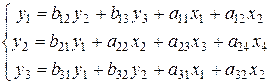
Проверим каждое уравнение системы на необходимое и достаточное условие идентификации.

1) Для первого уравнения 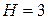(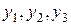), отсутствуют, т.е. , необходимое условие идентификации выдержано. Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при отсутствующих в первом уравнении переменных.

Уравнение	Переменные

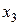
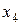
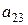
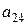
Определитель матрицы 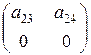равен нулю. Достаточное условие идентифицируемости не выполняется, и первое уравнение нельзя считать идентифицируемым.

2) Для второго уравнения 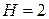(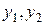), , 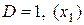т.е. , необходимое условие идентификации выдержано. Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при отсутствующих в втором уравнении переменных.

Уравнение	Переменные
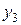
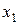
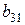
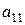
	-1

Определитель матрицы не равен нулю, следовательно, ранг матрицы равен 2, что не меньше числа эндогенных переменных в системе минус 1. Достаточное условие идентифицируемости выполняется, и второе уравнение точно идентифицируемо.

3) В третьем уравнении системы 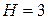и 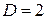. Необходимое условие выполняется. Рассматривая матрицу

Уравнение	Переменные

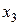
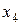
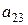
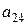
делаем вывод о невыполнении достаточного условия идентифицируемости. Уравнение неидентифицируемо.

Вывод: структурная модель неидентифицируема.

Пример 2.

Требуется:

Предположим, что следующая структурная модель признана идентифицируемой:

Исходя из приведенной формы (уравнения которой найдены через Анализ данных/Регрессия)

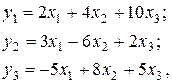
найти структурные коэффициенты модели.

1) Из третьего уравнения приведенной формы выразим 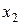(так как его нет в первом уравнении структурной формы)

.

Данное выражение содержит переменные 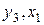и 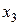, которые входят в правую часть первого уравнения структурной формы модели (СФМ). Подставим полученное выражение 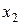в первое уравнение приведенной формы модели (ПФМ):

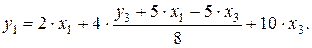
Откуда получим первое уравнение СФМ в виде

2) во втором уравнении СФМ нет переменных 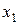и 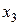. Структурные параметры второго уравнения СФМ можно определить в два этапа.

Первый этап: выразим 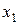в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения

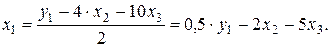
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует 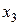, которого нет в СФМ.

Выразим 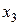из третьего уравнения ПФМ

.

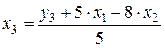Подставим его в выражение для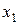

Второй этап: аналогично, чтобы выразить 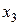через искомые 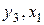и 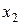, заменим в выражении 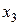значение 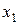на полученное из первого уравнения ПФМ

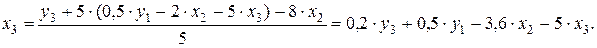
Следовательно,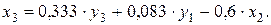

Подставим полученные 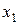и 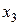во второе уравнение ПФМ

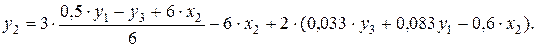
В результате получаем второе уравнение СФМ

3) из второго уравнения ПФМ выразим 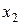, так как его нет в третьем уравнении СФМ

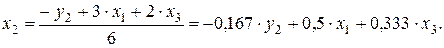
Подставим полученное выражение в третьем уравнении ПФМ

В результате получаем третье уравнение СФМ

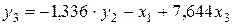
Таким образом, СФМ примет вид

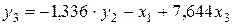
Пример 3.

Изучается модель вида

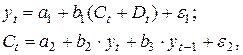
где 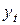- валовой национальный доход;

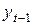- валовой национальный доход предшествующего года;

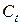- личное потребление;

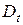- конечный спрос (помимо личного потребления);

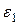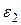и - случайные составляющие.

Информация за девять лет о приростах всех показателей дана в таблице.

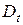
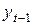
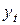
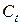
Год					Год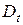
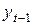
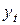
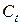
	-6,8	46,7	3,1	7,4		44,7	17,8	37,2	8,6
	22,4	3,1	22,8	30,4		23,1	37,2	35,7	30,0
	-17,3	22,8	7,8	1,3		51,2	35,7	46,6	31,4
	12,0	7,8	21,4	8,7		32,3	46,6	56,0	39,1
	5,9	21,4	17,8	25,8		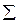167,5	239,1	248,4	182,7

Для данной модели была получена система приведенных уравнений

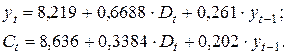
Необходимо:

1. Провести идентификацию модели.

2. Рассчитать параметры первого уравнения структурной модели.

1. В данной модели две эндогенные переменные (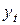 и 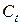) и две экзогенные переменные ( 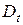и 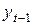). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1+1.

Первое уравнение сверхидентифицировано, так как в нем параметры пр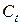и и 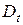наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная 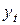. Переменная 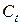в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной 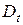. В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: 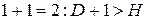. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверхидентифицирована.

2. Для определения параметров сверхидентифицированой модели используется двухшаговый метод наименьших квадратов.

Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 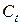. Для этого в приведенное уравнение

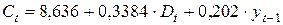
подставим значения 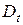и 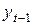, имеющиеся в условии задачи. Полученные значения обозначим .

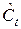Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 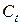на теоретические 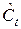и рассчитываем новую переменную .

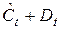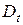
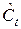
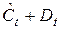
Год				Год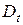
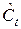
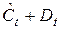
	-6,8	15,8	9,0		44,7	27,4	72,1
	22,4	16,8	39,2		23,1	24,0	47,1
	-17,3	7,4	-9,9		51,2	33,2	84,4
	12,0	14,3	26,3		32,3	29,0	61,3
	5,9	15,0	20,9		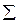167,5	182,9	350,4

Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 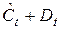через . Решаем уравнение . С помощью МНК получим 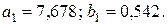Запишем первое уравнение структурной модели как

.

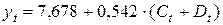Пример 3.

Рассматривается следующая модель:

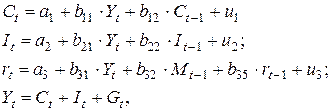
где 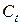- расходы на потребление в период ; 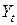- совокупный доход в период ; 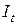- инвестиции в период ; 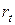- процентная ставка в период ; 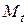- денежная масса в период ; 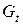- государственные расходы в период ; 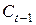- расходы на потребление в период 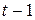; 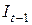- инвестиции в период 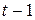; - случайные ошибки.

Решение:

В этой системе все уравнения сверхидентифицированы. Для оценки параметров каждого уравнения применяем двухшаговый МНК.

Шаг 1. Запишем приведенную форму модели в общем виде

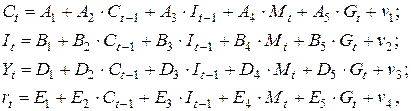
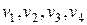- случайные ошибки.

Определим параметры каждого уравнения отдельно обычным МНК (Сервис/Анализ данных/Регрессия).

Затем по созданным уравнениям регрессии найдем расчетные значения эндогенных переменных 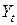и 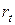. Обозначим их соответственно 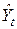и .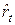

Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в роли факторных признаков, их расчетными значениями:

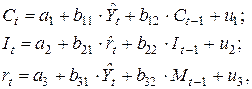
Применяем к каждому из полученных уравнений обычный МНК, заканчиваем процедуру параметризации.

Задания для самостоятельной работы

Необходимо:

1. Выделить эндогенные и экзогенные переменные.

2. Применив необходимое и достаточное условия идентификации, определить, идентифицировано ли каждое из уравнений системы.

3. Если система идентифицируется, записать приведенную форму модели.

4. Определить коэффициенты приведенной формы модели.

5. Определить коэффициенты структурной формы модели.

Примечание. Исходные статистические данные для факторов, используемых в моделях, брать из таблицы:

Поиск по сайту: