АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение регрессии по первым разностям

Читайте также:
  1. XI. Метод регрессии
  2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  3. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  4. В соответствии с первым критерием (субъектом) правосознание бывает общественным, групповым и индивидуальным.
  5. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  6. Волна вероятности. Уравнение Шредингера
  7. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  8. Временное и стационарное уравнение Шредингера. Решения.
  9. Вычисление и интерпретация параметров парной линейной регрессии
  10. Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля
  11. Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.
  12. Гипербола. Каноническое уравнение гиперболы и его свойства.

Ежегодные абсолютные приросты (первые разности) определяются по формулам , .

yt xt Δy Δx
       
       
       
       
       
       

Если ряды динамики характеризуются линейной тенденцией, то модель можно построить в виде . Для подтверждения линейной тенденции найдем по каждому ряду коэффициенты автокорреляции первого порядка.

r1 для у r1 для x
0,989571476 0,973773

Эти коэффициенты близки к единице, поэтому целесообразно моделировать взаимосвязь рядов по первым разностям. Если бы при невысоких значениях , достаточно высокими окажутся коэффициенты , есть смысл моделировать по вторым разностям .

Строим уравнение .

ВЫВОД ИТОГОВ          
           
Регрессионная статистика        
Множественный R 0,751809412        
R-квадрат 0,565217391        
Нормированный R-квадрат 0,420289855        
Стандартная ошибка 0,868114732        
Наблюдения          
           
Дисперсионный анализ        
  df SS MS F Значимость F
Регрессия   2,93913 2,93913 3,9 0,142772
Остаток   2,26087 0,753623    
Итого   5,2      
           
  Коэффициенты Стандартная ошибка t-статистика P-Значение  
a 2,565217391 1,101068 2,329754 0,102171  
b 0,565217391 0,286209 1,974842 0,142772  
           
           
           
ВЫВОД ОСТАТКА          
           
Наблюдение Предсказанное Y Остатки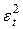  
  4,260869565 0,73913 0,546314    
  3,695652174 0,304348 0,092628 0,189036  
  4,826086957 0,173913 0,030246 0,017013  
  5,956521739 0,043478 0,00189 0,017013  
  4,260869565 -1,26087 1,589792 1,701323  
      2,26087 1,924386  

 

Выводы:

Ø Уравнение достоверно на 56,52%.

Ø Статистика критерия Фишера – 3,9; значимость F – 0,14, что превышает допустимый уровень значимости 0,05. Уравнение в целом признаем незначимым.

Ø Из коэффициентов регрессии ни один нельзя признать значимым. Уровень ошибки везде превышает 0,05.

Ø Статистика Дарбина-Уотсона 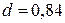. Критические значения критерия 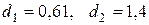. Поскольку выполняется неравенство , гипотеза о независимости остатков отклоняется, и модель признается неадекватной по данному критерию.

Вывод: таким образом, на данном этапе наиболее пригодным для прогнозирования считаем уравнение с включенным фактором времени.

 

Вариант 1     Вариант 2     Вариант 3     Вариант 4  
                             
Месяц x y   Месяц x y   Месяц x y   Месяц x y
  9,8 197,8     12,8 197,8     9,8 197,8     9,8 199,8
  13,0 188,9     14,0 188,9     12,0 189,9     13,0 188,9
  16,2 181,0     17,2 182,0     15,2 180,0     15,2 180,0
  19,4 172,1     18,4 171,1     16,4 172,1     18,4 173,1
  21,6 162,2     20,6 162,2     21,6 163,2     21,6 162,2
  20,7 155,4     21,7 154,4     20,7 155,4     23,7 155,4
  22,9 144,5     25,9 146,5     24,9 144,5     25,9 144,5
  27,1 135,6     25,1 137,6     26,1 135,6     26,1 135,6
  29,3 126,7     29,3 127,7     27,3 127,7     29,3 126,7
  29,5 117,8     32,5 119,8     30,5 119,8     32,5 119,8
  34,7 110,9     34,7 109,9     34,7 110,9     34,7 109,9
  33,8 100,1     36,8 102,1     36,8 100,1     35,8 100,1
  37,0 92,2     38,0 91,2     37,0 93,2     37,0 91,2
  40,2 83,3     39,2 83,3     38,2 82,3     39,2 82,3
  41,4 75,4     43,4 75,4             42,4 73,4
  43,6 65,5     45,6 66,5             43,6 66,5
          44,7 55,6             47,7 57,6
          46,9 47,7             49,9 47,7
          52,1 37,9             51,1 39,9
          53,3 30,0             53,3 30,0
                          55,5 21,1
                          56,7 12,2
                          60,8 4,3
                          63,0 -4,6
                             
                             
Вариант 5     Вариант 6     Вариант 7     Вариант 8  
                             
Месяц x y   Месяц x y   Месяц x y   Месяц x y
  11,8 199,8     9,8 197,8     12,8 198,8     9,8 197,8
  12,0 189,9     13,0 190,9     13,0 190,9     14,0 190,9
  16,2 182,0     16,2 182,0     17,2 181,0     14,2 181,0
  16,4 173,1     16,4 173,1     18,4 173,1     18,4 172,1
  21,6 164,2     21,6 162,2     20,6 163,2     20,6 162,2
  20,7 153,4     21,7 153,4     22,7 153,4     22,7 153,4
  22,9 146,5     25,9 146,5     23,9 144,5     24,9 146,5
  25,1 136,6     25,1 135,6     26,1 135,6     28,1 136,6
  28,3 127,7     27,3 128,7     29,3 128,7     29,3 128,7
  30,5 118,8     30,5 118,8     29,5 117,8     29,5 119,8
  31,7 110,9     31,7 110,9     31,7 110,9     32,7 108,9
  35,8 100,1     36,8 101,1     33,8 101,1     34,8 101,1
  38,0 92,2     39,0 91,2     36,0 92,2     36,0 92,2
  41,2 84,3     41,2 84,3     39,2 82,3     38,2 82,3
  43,4 73,4     42,4 75,4     42,4 75,4     42,4 73,4
  45,6 64,5     45,6 66,5     44,6 66,5     43,6 66,5
  47,7 55,6     47,7 55,6     47,7 56,6        
  47,9 48,7     47,9 46,7     46,9 47,7        
  50,1 38,9             51,1 37,9        
  53,3 29,0             53,3 30,0        
  55,5 22,1                        
  56,7 13,2                        
                             
                             
                             
Вариант 9     Вариант 10                  
                             
Месяц x y   Месяц x y                
  12,8 199,8     12,8 197,8                
  14,0 189,9     12,0 190,9                
  14,2 180,0     14,2 181,0                
  17,4 173,1     18,4 172,1                
  19,6 162,2     19,6 164,2                
  23,7 155,4     21,7 154,4                
  23,9 146,5     25,9 144,5                
  26,1 136,6     28,1 137,6                
  28,3 126,7     27,3 126,7                
  31,5 118,8     31,5 118,8                
  31,7 108,9     32,7 108,9                
  36,8 101,1     36,8 102,1                
  39,0 91,2     37,0 91,2                
  41,2 83,3     41,2 83,3                
          42,4 74,4                
          43,6 64,5                
          45,7 55,6                
          49,9 48,7                

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)