Нелинейные модели парной регрессии

Полином 2-го порядка: .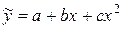

Параметры a, b и c находят, решая методом определителей систему уравнений:

Гипербола: .

Параметры a и b находят, решая систему уравнений

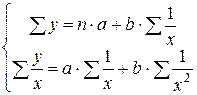
Регрессия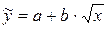

Система нормальных уравнений имеет вид:

.

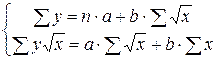Степенная функция: .

Пусть , , . Тогда уравнение примет вид

.

Параметры модели определяются по следующим формулам:

, .

Показательная функция: .

Пусть , , . Тогда уравнение регрессии примет вид 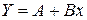. Параметры модели определяются по следующим формулам:

, .

Полулогарифмическая функция: .

Оценка параметров может быть найдена по формулам:

.

Логистическая функция: .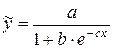

Обратная модель вида: .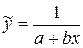

Оценка параметров может быть найдена по формулам:

.

Оценка тесноты связи в нелинейной регрессии:

а) индекс корреляции R,

,

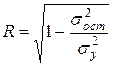где 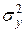– общая дисперсия результативного признака, 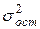– остаточная дисперсия.

Кроме того,

;

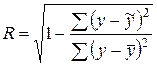Величина данного показателя находится в границах 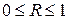, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

б) индекс детерминации 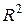имеет тот же смысл, что и коэффициент детерминации в линейных регрессионных моделях;

в) коэффициент средней эластичности 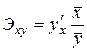, где 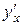– производная функции

Функция	Коэффициент средней эластичности
Парабола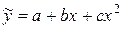
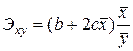
Гипербола
Показательная
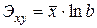
Степенная
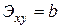
Экспоненциальная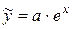
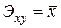
Полулогарифмическая
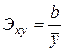
Логистическая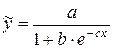
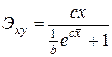
Обратная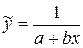

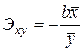
Поиск по сайту: