 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Обоснования возможности замены нелинейной регрессии линейной функцией
1) если величина 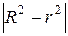 не превышает 0,1, то предположение о линейной форме связи считается оправданным;
не превышает 0,1, то предположение о линейной форме связи считается оправданным;
2) если  , то вычисляют ошибку разности между
, то вычисляют ошибку разности между 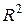 и
и 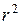
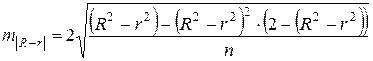
и t -критерий Стъюдента
 .
.
Если  , то различие между
, то различие между 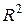 и
и 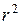 существенно, и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина
существенно, и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина 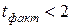 , то различие между
, то различие между 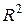 и
и 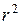 не существенно, и имеет смысл перейти к линейной регрессии.
не существенно, и имеет смысл перейти к линейной регрессии.
Практические рекомендации по выполнению расчетов
с помощью табличного редактора MS Excel
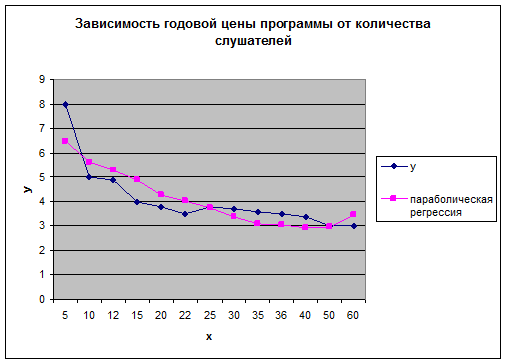
Имеются данные о годовой цене программы «Мастер делового администрирования» и числе слушателей в образовательном учреждении.
| Цена программы, тыс. долл., y | 4,9 | 3,8 | 3,5 | 3,8 | 3,7 | 3,6 | 3,5 | 3,4 | |||||
| Число слушателей, чел., x |
Необходимо:
1. Построить поле корреляции и сформулировать гипотезу о форме связи.
2. Рассчитать параметры параболической, степенной, показательной, полулогарифмической, обратной и гиперболической регрессий.
3. Постройте на одной диаграмме с полем корреляции линию регрессии.
4. В каждом случае оцените тесноту связи с помощью показателей корреляции и детерминации.
5. Оценить с помощью средней ошибки аппроксимации качество модели.
6. Оценить с помощью F -критерия Фишера статистическую надежность результатов регрессионного моделирования.
7. Выберите лучшее уравнение регрессии.
8. Дайте по выбранному уравнению оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности.
9. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его максимального в исходных данных значения. Определите доверительный интервал прогноза для уровня значимости 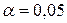 .
.
Полином 2-го порядка (парабола): 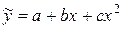 .
.
Параметры a, b и c находят, решая методом определителей систему уравнений:

Необходима вспомогательная таблица расчетов:
| y | x | 
| 
| 
| 
| 
| |
| 4,9 | 58,8 | 705,6 | |||||
| 3,8 | |||||||
| 3,5 | |||||||
| 3,8 | |||||||
| 3,7 | |||||||
| 3,6 | |||||||
| 3,5 | |||||||
| 3,4 | |||||||
| Сумма | 53,2 | 1285,8 | 43910,6 |
Получаем систему уравнений
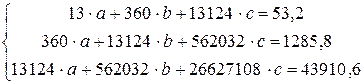
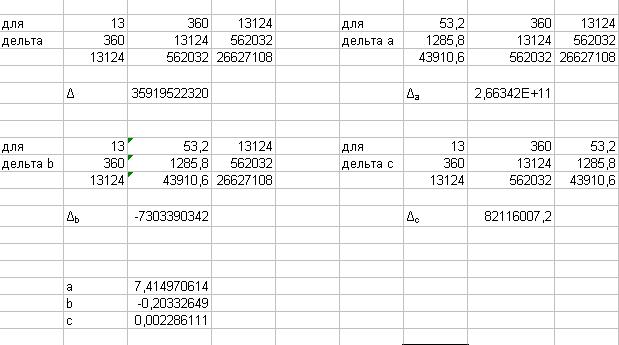
Ø Составим главный определитель системы, состоящий из коэффициентов при переменных a, b и c,
 .
.
Вычислить этот определитель можно в Excel, воспользовавшись математической функцией МОПРЕД.
Ø Далее составляем и вычисляем три вспомогательных определителя системы,  ;
;
 ,
,  ,
,
 .
.
Ø Находим параметры a, b и c соответственно по формулам  ,
, 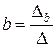 ,
,  .
.
Таким образом, уравнение параболической регрессии признаков x и y имеет вид:  .
.
Показателем тесноты связи выступает индекс корреляции 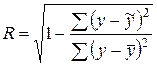 , коэффициент детерминации
, коэффициент детерминации 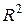 . Для расчета этих характеристик, а также для расчета средней ошибки аппроксимации необходимо составить в Excel расчетную таблицу следующего вида:
. Для расчета этих характеристик, а также для расчета средней ошибки аппроксимации необходимо составить в Excel расчетную таблицу следующего вида:
| y | x | 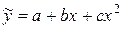
| 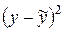
| 
| 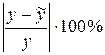
| |
| 6,455490941 | 2,38550823 | 15,27006 | 19,30636324 | |||
| 5,610316807 | 0,3724866 | 0,823905 | 12,20633613 | |||
| 4,9 | 5,304252704 | 0,16342025 | 0,652367 | 8,250055184 | ||
| 4,879448212 | 0,77342916 | 0,008521 | 21,98620529 | |||
| 3,8 | 4,262885156 | 0,21426267 | 0,085444 | 12,18118831 | ||
| 3,5 | 4,048265484 | 0,30059504 | 0,350828 | 15,66472813 | ||
| 3,8 | 3,760627639 | 0,00155018 | 0,085444 | 1,036114765 | ||
| 3,7 | 3,372675661 | 0,10714122 | 0,153905 | 8,846603755 | ||
| 3,6 | 3,099029222 | 0,25097172 | 0,242367 | 13,91585494 | ||
| 3,5 | 3,058016599 | 0,19534933 | 0,350828 | 12,62809717 | ||
| 3,4 | 2,939688322 | 0,21188684 | 0,47929 | 13,53857875 | ||
| 2,96392314 | 0,00130154 | 1,193136 | 1,202562007 | |||
| 3,445380113 | 0,19836345 | 1,193136 | 14,84600377 | |||
| Среднее | 4,092308 | 11,96989934 | ||||
| Сумма | 5,17626623 | 20,88923 |
Тогда  ,
,  ,
,  .
.
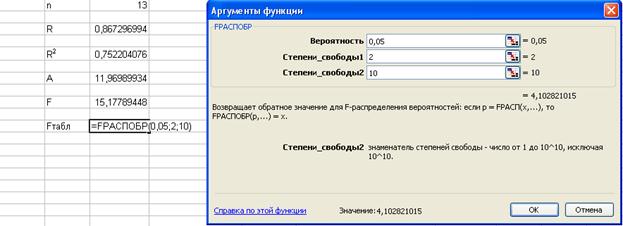
Расчетное значение критерия Фишера равно  , где n – число наблюдений, m – число параметров при переменной x. Для параболы
, где n – число наблюдений, m – число параметров при переменной x. Для параболы  , в данном примере
, в данном примере  .
.
Выводы:
Ø 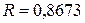 , что говорит о тесной прямой связи между признаками x и y.
, что говорит о тесной прямой связи между признаками x и y.
Ø  , т.е. 75,22% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
, т.е. 75,22% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 15,18, оно превышает соответствующее табличное (критическое) значение (4,1). Найденное уравнение параболической регрессии статистически надежно.
Графическая иллюстрация приведена ниже
Степенная функция:  .
.
Пусть  ,
,  ,
,  . Тогда уравнение примет вид
. Тогда уравнение примет вид
 .
.
Параметры модели определяются по следующим формулам:
 ,
,  .
.
Составим вспомогательную таблицу.
| y | x | 
| 
| 
| 
| |
| 2,079441542 | 1,60943791 | 2,59029 | 3,3467321 | |||
| 1,609437912 | 2,30258509 | 5,301898 | 3,7058677 | |||
| 4,9 | 1,589235205 | 2,48490665 | 6,174761 | 3,9491011 | ||
| 1,386294361 | 2,7080502 | 7,333536 | 3,7541547 | |||
| 3,8 | 1,335001067 | 2,99573227 | 8,974412 | 3,9993058 | ||
| 3,5 | 1,252762968 | 3,09104245 | 9,554543 | 3,8723435 | ||
| 3,8 | 1,335001067 | 3,21887582 | 10,36116 | 4,2972027 | ||
| 3,7 | 1,30833282 | 3,40119738 | 11,56814 | 4,4498982 | ||
| 3,6 | 1,280933845 | 3,55534806 | 12,6405 | 4,5541657 | ||
| 3,5 | 1,252762968 | 3,58351894 | 12,84161 | 4,4892998 | ||
| 3,4 | 1,223775432 | 3,68887945 | 13,60783 | 4,51436 | ||
| 1,098612289 | 3,91202301 | 15,30392 | 4,2977965 | |||
| 1,098612289 | 4,09434456 | 16,76366 | 4,4980973 | |||
| Среднее | 4,092308 | 27,69230769 | 1,373092597 | 3,12661091 | 10,23202 | 4,1329481 |
  
| ||||||
| b | -0,35101802 | |||||
| A | 2,470589356 | |||||
| a | 11,82941654 | |||||
Степенная регрессия имеет вид:  . Для оценки тесноты связи и надежности моделирования составим расчетную таблицу
. Для оценки тесноты связи и надежности моделирования составим расчетную таблицу
| y | x | 
| 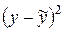
| 
| 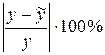
| |
| 6,72376088 | 1,62878629 | 15,27006 | 15,952989 | |||
| 5,271634701 | 0,07378541 | 0,823905 | 5,432694022 | |||
| 4,9 | 4,944828847 | 0,00200963 | 0,652367 | 0,914874437 | ||
| 4,572293534 | 0,32751989 | 0,008521 | 14,30733836 | |||
| 3,8 | 4,13312325 | 0,1109711 | 0,085444 | 8,766401326 | ||
| 3,5 | 3,997134646 | 0,24714286 | 0,350828 | 14,20384702 | ||
| 3,8 | 3,821740509 | 0,00047265 | 0,085444 | 0,572118651 | ||
| 3,7 | 3,584818332 | 0,01326682 | 0,153905 | 3,11301806 | ||
| 3,6 | 3,395999538 | 0,04161619 | 0,242367 | 5,666679501 | ||
| 3,5 | 3,362583734 | 0,01888323 | 0,350828 | 3,926179017 | ||
| 3,4 | 3,240495363 | 0,02544173 | 0,47929 | 4,691312861 | ||
| 2,996361745 | 1,3237E-05 | 1,193136 | 0,121275157 | |||
| 2,810607494 | 0,03586952 | 1,193136 | 6,31308354 | |||
| Среднее | 4,092308 | 6,460139305 | ||||
| Сумма | 2,52577855 | 20,88923 |
Пользуясь формулами для расчета, получим
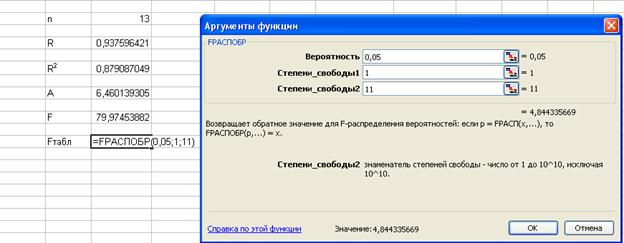
Примечание. При вычислении статистики Фишера для степенной функции параметр m =1.
Выводы:
Ø  , что говорит о тесной прямой связи между признаками x и y.
, что говорит о тесной прямой связи между признаками x и y.
Ø 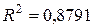 , т.е. 87,91% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
, т.е. 87,91% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 79,97, оно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение степенной регрессии статистически надежно.
Графическая иллюстрация приведена ниже
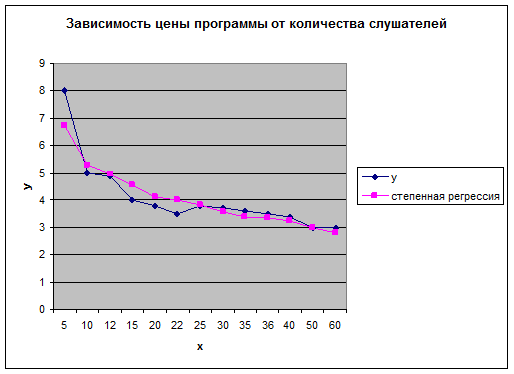
Показательная функция:  .
.
Пусть  ,
,  ,
,  . Тогда уравнение регрессии примет вид
. Тогда уравнение регрессии примет вид 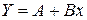 . Параметры модели определяются по следующим формулам:
. Параметры модели определяются по следующим формулам:
 ,
,  .
.
Составим вспомогательную таблицу.
| y | x | 
| 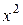
| 
| |
| 2,079441542 | 10,39721 | ||||
| 1,609437912 | 16,09438 | ||||
| 4,9 | 1,589235205 | 19,07082 | |||
| 1,386294361 | 20,79442 | ||||
| 3,8 | 1,335001067 | 26,70002 | |||
| 3,5 | 1,252762968 | 27,56079 | |||
| 3,8 | 1,335001067 | 33,37503 | |||
| 3,7 | 1,30833282 | 39,24998 | |||
| 3,6 | 1,280933845 | 44,83268 | |||
| 3,5 | 1,252762968 | 45,09947 | |||
| 3,4 | 1,223775432 | 48,95102 | |||
| 1,098612289 | 54,93061 | ||||
| 1,098612289 | 65,91674 | ||||
| Среднее | 4,092308 | 27,69230769 | 1,373092597 | 1009,53846 | 34,84409 |
 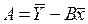
| |||||
| B | -0,01310402 | ||||
| A | 1,735973264 | ||||
| b | 0,98698146 | 
| 
| ||
| a | 5,674447852 |
Показательная регрессия имеет вид: 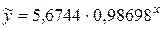 .
.
Для оценки тесноты связи и надежности моделирования составим расчетную таблицу
| y | x | 
| 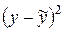
| 
| 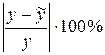
| |
| 5,314575517 | 7,21150465 | 15,27006 | 33,56780603 | |||
| 5,271634701 | 0,07378541 | 0,823905 | 5,432694022 | |||
| 4,9 | 4,944828847 | 0,00200963 | 0,652367 | 0,914874437 | ||
| 4,572293534 | 0,32751989 | 0,008521 | 14,30733836 | |||
| 3,8 | 4,13312325 | 0,1109711 | 0,085444 | 8,766401326 | ||
| 3,5 | 3,997134646 | 0,24714286 | 0,350828 | 14,20384702 | ||
| 3,8 | 3,821740509 | 0,00047265 | 0,085444 | 0,572118651 | ||
| 3,7 | 3,584818332 | 0,01326682 | 0,153905 | 3,11301806 | ||
| 3,6 | 3,395999538 | 0,04161619 | 0,242367 | 5,666679501 | ||
| 3,5 | 3,362583734 | 0,01888323 | 0,350828 | 3,926179017 | ||
| 3,4 | 3,240495363 | 0,02544173 | 0,47929 | 4,691312861 | ||
| 2,996361745 | 1,3237E-05 | 1,193136 | 0,121275157 | |||
| 2,810607494 | 0,03586952 | 1,193136 | 6,31308354 | |||
| Среднее | 4,092308 | 7,81512523 | ||||
| Сумма | 8,10849691 | 20,88923 |
Пользуясь формулами для расчета, получим
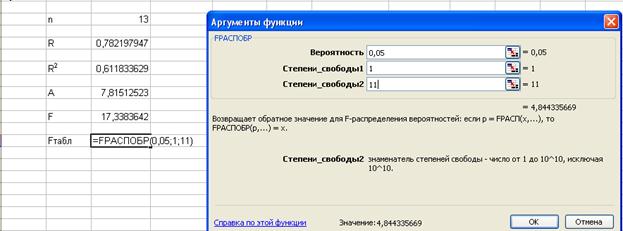
Выводы:
Ø  , что говорит о тесной прямой связи между признаками x и y.
, что говорит о тесной прямой связи между признаками x и y.
Ø  , т.е. 61,18% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
, т.е. 61,18% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 17,34, оно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение показательной регрессии статистически надежно.
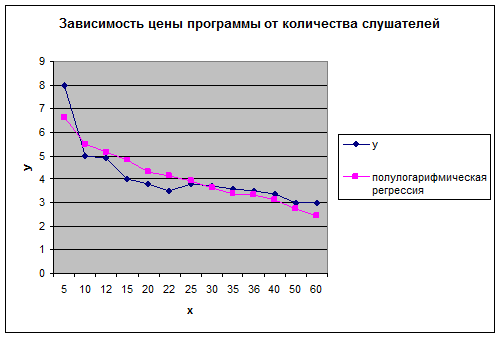
Графическая иллюстрация приведена ниже.
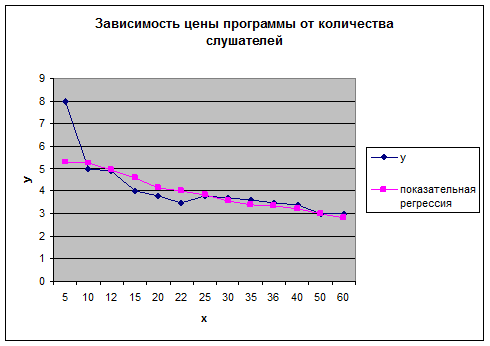
Полулогарифмическая функция:  .
.
Оценка параметров может быть по решению системы уравнений:
 .
.
| y | x | 
| 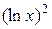
| 
| |
| 1,609437912 | 2,59029039 | 12,8755 | |||
| 2,302585093 | 5,30189811 | 11,51293 | |||
| 4,9 | 2,48490665 | 6,17476106 | 12,17604 | ||
| 2,708050201 | 7,33353589 | 10,8322 | |||
| 3,8 | 2,995732274 | 8,97441185 | 11,38378 | ||
| 3,5 | 3,091042453 | 9,55454345 | 10,81865 | ||
| 3,8 | 3,218875825 | 10,3611616 | 12,23173 | ||
| 3,7 | 3,401197382 | 11,5681436 | 12,58443 | ||
| 3,6 | 3,555348061 | 12,6404998 | 12,79925 | ||
| 3,5 | 3,583518938 | 12,841608 | 12,54232 | ||
| 3,4 | 3,688879454 | 13,6078316 | 12,54219 | ||
| 3,912023005 | 15,303924 | 11,73607 | |||
| 4,094344562 | 16,7636574 | 12,28303 | |||
| Сумма | 53,2 | 40,64594181 | 133,016267 | 156,3181 |
Получаем систему уравнений
 .
.
Решить эту систему можно любым доступным способом, например, методом подстановки. При использовании Excel это лучше сделать методом определителей.
| Для | 40,64594181 | Для | 53,2 | 40,64594181 | ||
| дельта | 40,64594 | 133,0162668 | дельта a | 156,318124 | 133,0162668 | |
| Δ | 77,11888 | Δa | 722,768022 | |||
| Для | 53,2 | |||||
| дельта b | 40,64594 | 156,318124 | a | 9,37212778 | ||
| b | -1,6886719 | |||||
| Δb | -130,228493 |
Уравнение полулогарифмической регрессии имеет вид:  .
.
Для оценки тесноты связи и надежности моделирования составим расчетную таблицу
| y | x | 
| 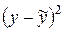
| 
| 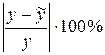
| |
| 6,654315149 | 1,81086772 | 15,2700592 | 16,82106064 | |||
| 5,483816959 | 0,23407885 | 0,82390533 | 9,676339186 | |||
| 4,9 | 5,175935664 | 0,07614049 | 0,65236686 | 5,631340072 | ||
| 4,799119411 | 0,63859183 | 0,00852071 | 19,97798528 | |||
| 3,8 | 4,31331877 | 0,26349616 | 0,08544379 | 13,50838868 | ||
| 3,5 | 4,152371144 | 0,42558811 | 0,3508284 | 18,63917555 | ||
| 3,8 | 3,936502518 | 0,01863294 | 0,08544379 | 3,59217152 | ||
| 3,7 | 3,628621222 | 0,00509493 | 0,15390533 | 1,929156163 | ||
| 3,6 | 3,368311295 | 0,05367966 | 0,24236686 | 6,435797348 | ||
| 3,5 | 3,320739926 | 0,03213417 | 0,3508284 | 5,121716394 | ||
| 3,4 | 3,142820581 | 0,06614125 | 0,47928994 | 7,564100572 | ||
| 2,766004328 | 0,05475397 | 1,19313609 | 7,799855721 | |||
| 2,458123033 | 0,29363065 | 1,19313609 | 18,06256558 | |||
| Среднее | 4,092308 | 10,36612713 | ||||
| Сумма | 3,97283074 | 20,8892308 |
Пользуясь формулами для расчета, получим
| n | Ø  , что говорит о тесной прямой связи между признаками x и y.
Ø , что говорит о тесной прямой связи между признаками x и y.
Ø 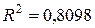 , т.е. 80,98% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 46,84, оно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение полулогарифмической регрессии статистически надежно. , т.е. 80,98% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 46,84, оно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение полулогарифмической регрессии статистически надежно.
| |
| R | 0,899896887 | |
| R2 | 0,809814407 | |
| A | 10,36612713 | |
| F | 46,83824022 | |
| Fтабл | 4,844335669 |
Обратная модель вида: 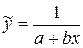 .
.
Оценка параметров может быть найдена по решению системы:
 .
.
| y | x | 
| 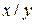
| 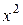
| |
| 0,125 | 0,625 | ||||
| 0,2 | |||||
| 4,9 | 0,20408163 | 2,44897959 | |||
| 0,25 | 3,75 | ||||
| 3,8 | 0,26315789 | 5,26315789 | |||
| 3,5 | 0,28571429 | 6,28571429 | |||
| 3,8 | 0,26315789 | 6,57894737 | |||
| 3,7 | 0,27027027 | 8,10810811 | |||
| 3,6 | 0,27777778 | 9,72222222 | |||
| 3,5 | 0,28571429 | 10,2857143 | |||
| 3,4 | 0,29411765 | 11,7647059 | |||
| 0,33333333 | 16,6666667 | ||||
| 0,33333333 | |||||
| Сумма | 53,2 | 3,38565836 | 103,499216 |
Получаем систему уравнений:
 .
.
Решение этой системы и остальные выводы по данной регрессии представлены далее.
| Для | Для | 3,38565836 | ||||
| дельта | дельта a | 103,499216 | ||||
| Δ | Δa | 7173,66239 | ||||
| Для | 3,385658355 | |||||
| дельта b | 103,4992163 | a | 0,17491618 | |||
| b | 0,00308819 | |||||
| Δb | 126,6528041 |
Уравнение обратной регрессии имеет вид:  .
.
| y | x | 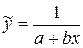
| 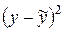
| 
| 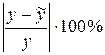
| |
| 5,253283798 | 7,54444989 | 15,2700592 | 34,33395252 | |||
| 4,859132073 | 0,01984377 | 0,82390533 | 2,817358541 | |||
| 4,9 | 4,717549745 | 0,0332881 | 0,65236686 | 3,723474587 | ||
| 4,519998446 | 0,27039838 | 0,00852071 | 12,99996116 | |||
| 3,8 | 4,225114815 | 0,18072261 | 0,08544379 | 11,18723198 | ||
| 3,5 | 4,11766073 | 0,38150478 | 0,3508284 | 17,64744942 | ||
| 3,8 | 3,966351012 | 0,02767266 | 0,08544379 | 4,37765821 | ||
| 3,7 | 3,737453631 | 0,00140277 | 0,15390533 | 1,012260294 | ||
| 3,6 | 3,533534037 | 0,00441772 | 0,24236686 | 1,846276747 | ||
| 3,5 | 3,495391553 | 2,1238E-05 | 0,3508284 | 0,13166991 | ||
| 3,4 | 3,350715313 | 0,00242898 | 0,47928994 | 1,449549627 | ||
| 3,036508307 | 0,00133286 | 1,19313609 | 1,216943553 | |||
| 2,7761775 | 0,05009651 | 1,19313609 | 7,460750006 | |||
| Среднее | 4,092308 | 7,708041274 | ||||
| Сумма | 8,51758027 | 20,8892308 |
| n | Ø 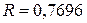 , что говорит о тесной прямой связи между признаками x и y.
Ø , что говорит о тесной прямой связи между признаками x и y.
Ø  , т.е.59,23% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 15,98, оно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение обратной регрессии статистически надежно. , т.е.59,23% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 15,98, оно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение обратной регрессии статистически надежно.
| |
| R | 0,769577917 | |
| R2 | 0,592250171 | |
| A | 7,708041274 | |
| F | 15,97732585 | |
| Fтабл | 4,844335669 |
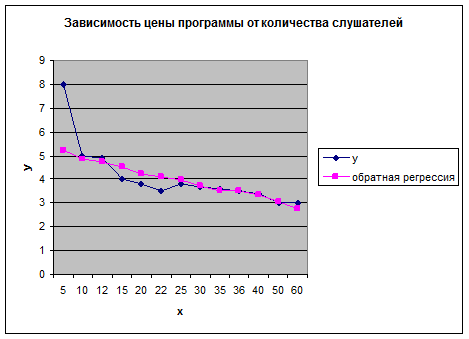
Гипербола:  .
.
Параметры a и b находят, решая систему уравнений
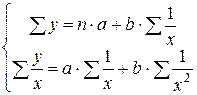 .
.
| y | x | 1/ x | 
| y/ x | |
| 0,2 | 0,04 | 1,6 | |||
| 0,1 | 0,01 | 0,5 | |||
| 4,9 | 0,083333333 | 0,00694444 | 0,40833333 | ||
| 0,066666667 | 0,00444444 | 0,26666667 | |||
| 3,8 | 0,05 | 0,0025 | 0,19 | ||
| 3,5 | 0,045454545 | 0,00206612 | 0,15909091 | ||
| 3,8 | 0,04 | 0,0016 | 0,152 | ||
| 3,7 | 0,033333333 | 0,00111111 | 0,12333333 | ||
| 3,6 | 0,028571429 | 0,00081633 | 0,10285714 | ||
| 3,5 | 0,027777778 | 0,0007716 | 0,09722222 | ||
| 3,4 | 0,025 | 0,000625 | 0,085 | ||
| 0,02 | 0,0004 | 0,06 | |||
| 0,016666667 | 0,00027778 | 0,05 | |||
| Сумма | 53,2 | 0,736803752 | 0,07155682 | 3,79450361 |
Система имеет вид:
 .
.
| Для | 0,736803752 | Для | 53,2 | 0,736803752 | ||
| дельта | 0,736804 | 0,071556825 | дельта a | 3,79450361 | 0,071556825 | |
| Δ | 0,387359 | Δa | 1,01101859 | |||
| Для | 53,2 | |||||
| дельта b | 0,736804 | 3,794503608 | a | 2,61003025 | ||
| b | 26,1529704 | |||||
| Δb | 10,1305873 |
Уравнение гиперболической регрессии имеет вид:
 .
.
| y | x | 
| 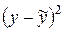
| 
| 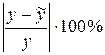
| |
| 5,253283798 | 7,54444989 | 15,2700592 | 34,33395252 | |||
| 4,859132073 | 0,01984377 | 0,82390533 | 2,817358541 | |||
| 4,9 | 4,717549745 | 0,0332881 | 0,65236686 | 3,723474587 | ||
| 4,519998446 | 0,27039838 | 0,00852071 | 12,99996116 | |||
| 3,8 | 4,225114815 | 0,18072261 | 0,08544379 | 11,18723198 | ||
| 3,5 | 4,11766073 | 0,38150478 | 0,3508284 | 17,64744942 | ||
| 3,8 | 3,966351012 | 0,02767266 | 0,08544379 | 4,37765821 | ||
| 3,7 | 3,737453631 | 0,00140277 | 0,15390533 | 1,012260294 | ||
| 3,6 | 3,533534037 | 0,00441772 | 0,24236686 | 1,846276747 | ||
| 3,5 | 3,495391553 | 2,1238E-05 | 0,3508284 | 0,13166991 | ||
| 3,4 | 3,350715313 | 0,00242898 | 0,47928994 | 1,449549627 | ||
| 3,036508307 | 0,00133286 | 1,19313609 | 1,216943553 | |||
| 2,7761775 | 0,05009651 | 1,19313609 | 7,460750006 | |||
| Среднее | 4,092308 | 7,708041274 | ||||
| Сумма | 8,51758027 | 20,8892308 |
| n | Ø  , что говорит об очень тесной прямой связи между признаками x и y.
Ø , что говорит об очень тесной прямой связи между признаками x и y.
Ø 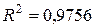 , т.е.97,56% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 440,57 оно существенно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение обратной регрессии статистически надежно. , т.е.97,56% вариации признака y объясняется за счет признака x данным уравнением регрессии, что является весьма удовлетворительным.
Ø Средняя ошибка аппроксимации не превышает установленного предела в 15%, что свидетельствует о хорошем качестве модели.
Ø Расчетное значение критерия Фишера равно 440,57 оно существенно превышает соответствующее табличное (критическое) значение (4,8). Найденное уравнение обратной регрессии статистически надежно.
| |
| R | 0,987745189 | |
| R2 | 0,975640558 | |
| A | 4,638171373 | |
| F | 440,5702713 | |
| Fтабл | 4,844335669 |

Сравним результата регрессионного анализа по разным видам парных регрессий:
| Регрессия | Коэффициент детерминации | Средняя ошибка аппроксимации |
| Парабола | 
| 
|
| Степенная | 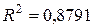
| 
|
| Показательная | 
| 
|
| Полулогарифмическая | 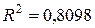
| 
|
| Обратная | 
| 
|
| Гипербола | 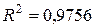
| 
|
| Линейная | 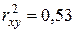
| 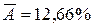
|
Все уравнения достаточно хорошо описывают исходные данные. Однако предпочтение можно отдать гиперболе  , для которой значение коэффициента детерминации наибольшее, а ошибка аппроксимации наименьшая.
, для которой значение коэффициента детерминации наибольшее, а ошибка аппроксимации наименьшая.
Дадим по выбранному уравнению количественную оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности. Для гиперболы он вычисляется по формуле  , т.е.
, т.е.  . Следовательно, при увеличении количества слушателей программы (фактора x) на 1% цена программы (фактор y) уменьшится на 0,23%.
. Следовательно, при увеличении количества слушателей программы (фактора x) на 1% цена программы (фактор y) уменьшится на 0,23%.
Рассчитаем прогнозное значение результата y, если прогнозное значение фактора x увеличится на 10% от его максимального в исходных данных значения.
 (чел).
(чел).
 (тыс. долл.)
(тыс. долл.)
Определим доверительный интервал прогноза для уровня значимости 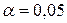 . Для этого найдем среднюю ошибку прогноза
. Для этого найдем среднюю ошибку прогноза 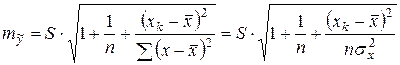 ,
,
где  – остаточная дисперсия,
– остаточная дисперсия, 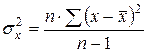 –дисперсия фактора x.
–дисперсия фактора x.
Составим расчетную таблицу
| y | x | 
| 
| 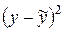
| |
| 514,9408284 | 7,84062433 | 0,0254006 | |||
| 313,0177515 | 5,22532729 | 0,05077239 | |||
| 4,9 | 246,2485207 | 4,78944445 | 0,01222253 | ||
| 161,0946746 | 4,35356161 | 0,12500581 | |||
| 3,8 | 59,17159763 | 3,91767877 | 0,01384829 | ||
| 3,5 | 32,40236686 | 3,79880163 | 0,08928242 | ||
| 3,8 | 7,24852071 | 3,65614907 | 0,02069309 | ||
| 3,7 | 5,325443787 | 3,48179593 | 0,04761301 | ||
| 3,6 | 53,40236686 | 3,35725798 | 0,05892369 | ||
| 3,5 | 69,01775148 | 3,33650165 | 0,02673171 | ||
| 3,4 | 151,4792899 | 3,26385451 | 0,01853559 | ||
| 497,6331361 | 3,13308966 | 0,01771286 | |||
| 1043,786982 | 3,04591309 | 0,00210801 | |||
| Сумма | 53,2 | 3154,769231 | 53,2 | 0,50885001 |
Тогда
 ;
; 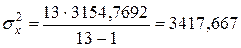 ;
;
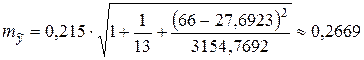 .
.
Предельная ошибка прогнозируемой стоимости программы составит
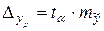 , где
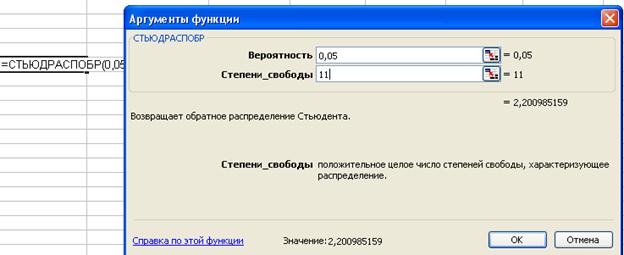
, где  – соответствующее табличное значение критерия Стъюдента.
– соответствующее табличное значение критерия Стъюдента.
По функции СТЪЮДРАСПОБР  .
. 
Доверительный интервал прогнозируемой стоимости программы составит:
 (тыс. долл.),
(тыс. долл.),
т.е. при 66 слушателях курса стоимость с вероятностью 95% будет не меньше 2,42 и не больше 3,58 тыс. долл.
Задания для самостоятельной работы
Вариант 1
Имеются данные о цене однокомнатной квартиры и величине ее общей площади по 10 сделкам одного района города:
| № п/п | ||||||||||
| Цена квартиры, тыс.долл. | ||||||||||
Площадь, 
|
Вариант 2
Имеются данные по 10 хозяйствам:
| Номер хозяйства | Урожайность, ц/га, y | Внесено удобрений, кг/га, х |
| 2,1 | ||
| 3,6 | ||
| 3,5 | ||
| 5,0 | ||
| 6,5 | ||
| 4,2 | ||
| 6,3 | ||
| 4,0 | ||
| 6,0 | ||
| 7,5 |
Вариант 3
По 17 регионам страны изучается зависимость ежемесячного среднедушевого денежного дохода у от удельного веса населения в трудоспособном возрасте в общей численности населения, х:
| Номер региона | Удельный вес населения в трудоспособном возрасте в общей численности населения, %, х | Среднедушевой ежемесячный денежный доход, тыс. руб., у |
| 60,6 | 3,4 | |
| 59,6 | 3,1 | |
| 60,8 | 3,7 | |
| 59,4 | 3,4 | |
| 60,4 | 3,6 | |
| 60,8 | 3,3 | |
| 60,6 | 3,1 | |
| 59,3 | 3,3 | |
| 60,3 | 3,6 | |
| 62,3 | 4,7 | |
| 60,2 | 3,2 | |
| 59,0 | 3,3 | |
| 61,4 | 4,1 | |
| 58,9 | 3,4 | |
| 59,0 | 3,2 | |
| 59,2 | 3,4 | |
| 61,0 | 3,9 |
Вариант 4
По 26 регионам страны изучается зависимость ожидаемой продолжительности жизни при рождении (лет) у от уровня заболеваемости детей в возрасте 0-14 лет на тыс. человек, х:
Поиск по сайту: