АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение линейной регрессии по уровням временных рядов

Читайте также:
  1. XI. Метод регрессии
  2. Авторегрессионные модели временных рядов
  3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  4. Анализ вариационных рядов
  5. Анализ взаимосвязи двух временных рядов
  6. Анализ временных рядов
  7. Анализ динамики временных рядов
  8. Арабских странах является наличие временных конституций, дей-
  9. Арифметика рядов Фибоначчи
  10. Арифметические выражения и алгоритм линейной структуры
  11. Биотехнология как наука может рассматриваться в двух временных и сущностных измерениях: современном и традиционном, классическом.
  12. Боевое крещение штурмовых отрядов

Уравнение регрессии и все статистические параметры получим по Анализ данных/Регрессия. Причем, в диалоговом окне ввода данных и параметров вывода можно поставить флажок на позиции Остатки, чтобы сразу получить значения :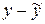

ВЫВОД ИТОГОВ        
           
Регрессионная статистика        
Множественный R 0,991706944        
R-квадрат 0,983482664        
Нормированный R-квадрат 0,97935333        
Стандартная ошибка 1,27038632        
Наблюдения          
           
Дисперсионный анализ        
  df SS MS F Значимость F
Регрессия   384,3778 384,377807 238,16 0,000103
Остаток   6,455526 1,613881402    
Итого   390,8333      
           
  Коэффициенты Стандартная ошибка t-статистика P-Значение  
Y-пересечение -93,21832884 8,766333 -10,6336741 0,000443  
Доход, % к 1985 г 1,246630728 0,080778 15,43275083 0,000103  
           
           
           
ВЫВОД ОСТАТКА        
           
Наблюдение Предсказанное Расход, руб Остатки ε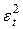  
  31,44474394 -1,44474 2,087285039    
  35,18463612 -0,18464 0,034090496 1,587872  
  37,67789757 1,322102 1,747954825 2,270261  
  42,66442049 1,33558 1,78377264 0,000182  
  50,14420485 -0,1442 0,020795039 2,189762  
  53,88409704 -0,8841 0,781627567 0,54744  
Сумма     6,455525606 6,595517  

 

Выводы:

Ø Уравнение достоверно на 98%.

Ø Статистика критерия Фишера – 238,16; значимость F – 0,000103, что не превышает допустимый уровень значимости 0,05. Уравнение в целом признаем значимым.

Ø Статистики критерия Стъюдента для коэффициентов регрессии также имеют допустимый уровень ошибки (P- значение) и признаются значимыми.

Найдем коэффициенты автокорреляции остатков до порядка. Поскольку в этой задаче 6 наблюдений, ищем для ряда остатков с помощью функции Коррел.

r1 r2
0,314389 -0,88749

Вывод: коэффициент автокорреляции второго порядка достаточно высок, что может указывать на невозможность использования линейного уравнения регрессии для прогнозирования.

Для окончательно проверки остатков регрессии на автокорреляцию, рассчитаем значение d -статистики Дарбина-Уотсона , получаем . Критические значения критерия (по таблице) . Поскольку выполняется неравенство , гипотеза о независимости остатков отклоняется, и модель признается неадекватной по данному критерию.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)