 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Парная линейная регрессия

Предварительные расчеты:
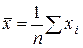 ;
; 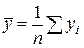 ;
; 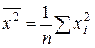 ;
;  ;
; 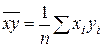 ;
;
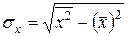 ;
; 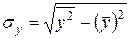 .
.
Построение таблицы вида
| x | y | xy | 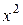
| 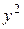
| |
| ………… | ………. | ……… | …….. | ……… | ……… |
| Среднее значение |
Формулы для расчетов параметров:
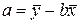 ,
, 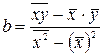 .
.
При компьютерном подборе в Excel можно использовать встроенную функцию Линейн
Оценка тесноты связи:
а) коэффициент корреляции 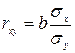 , или
, или 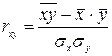 .
.
Если
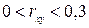 , то связь между признаками практически отсутствует;
, то связь между признаками практически отсутствует;
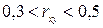 , связь между признаками слабая;
, связь между признаками слабая;
 , связь между признаками умеренная;
, связь между признаками умеренная;
 , связь между признаками сильная.
, связь между признаками сильная.
При компьютерном анализе можно использовать встроенную функцию Коррел.
б) коэффициент эластичности  показывает, на сколько процентов изменится результативный признак при изменении факторного признака на 1%;
показывает, на сколько процентов изменится результативный признак при изменении факторного признака на 1%;
в) коэффициент детерминации  показывает, какая доля вариации результативного признака y учтена в модели и обусловлена влиянием на нее изменением переменной x. Чем больше доля объясненной вариации, тем лучше линейная модель аппроксимирует исходные данные и ей можно воспользоваться для прогноза значений результативного признака.
показывает, какая доля вариации результативного признака y учтена в модели и обусловлена влиянием на нее изменением переменной x. Чем больше доля объясненной вариации, тем лучше линейная модель аппроксимирует исходные данные и ей можно воспользоваться для прогноза значений результативного признака.
Оценка значимости уравнения регрессии в целом:
Предварительные расчеты с построением таблицы вида
| x | y | 
| 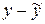
| 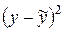
| 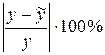
| |
| ………… | ………. | ……… | …….. | ……… | ……… |
а) F -критерий Фишера при числе степеней свободы 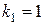 и
и 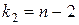 и уровне значимости 0,05. Расчетное значение критерия:
и уровне значимости 0,05. Расчетное значение критерия:
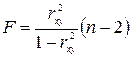 .
.
Критическое значение критерия берется из специальной таблицы критических точек распределения Фишера-Снедекора в приложениях к учебникам по теории вероятностей, статистике и эконометрике. При компьютерном анализе критическое значение можно найти с помощью функции FРАСПОБР.
Если расчетное значение F- критерия больше критического, нулевая гипотеза об отсутствии значимой связи признаков x и y отклоняется, и делается вывод о существенности этой связи.
б) Средняя ошибка аппроксимации
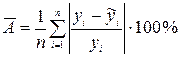 .
.
Оценка значимости параметров регрессии  :
:
а) Стандартная ошибка параметра a рассчитывается по формуле
 , где
, где 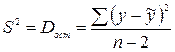 – остаточная дисперсия признака y.
– остаточная дисперсия признака y.
б) Стандартная ошибка коэффициента регрессии b рассчитывается по формуле
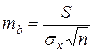 .
.
в) Стандартная ошибка коэффициента корреляции 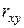 рассчитывается по формуле
рассчитывается по формуле
 .
.
Для проверки нулевой гипотезы о несущественности найденного параметра регрессии применяют t -критерий Стьюдента при числе степеней свободы 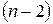 и уровне значимости 0,05.
и уровне значимости 0,05.
Расчетные значения t -статистики вычисляются по формулам:
 ,
, 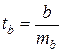 ,
, 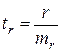 .
.
Критическое значение берется из специальной таблицы критических точек распределения Стьюдента в приложениях к учебникам по теории вероятностей и эконометрике. При компьютерном анализе критическое значение можно найти с помощью функции СТЬЮДРАСПОБР.
Если расчетное значение по абсолютной величине превышает табличное, гипотезу о несущественности параметра регрессии можно отклонить, параметр признается значимым.
Связь между F -критерием Фишера и t -критерием Стьюдента выражается равенством
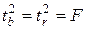 .
.
Расчет доверительных интервалов для параметров регрессии:
Доверительный интервал для параметра a определяется как  ;
;
доверительный интервал для коэффициента регрессииопределяется как  .
.
При компьютерном анализе использовать в Excel использовать путь Сервис/Анализ данных/Регрессия.
Интервальный прогноз на основе линейного уравнения регрессии:
Пусть  – прогнозное значение факторного признака;
– прогнозное значение факторного признака; 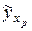 – точечный прогноз результативного признака. Тогда
– точечный прогноз результативного признака. Тогда
а) средняя ошибка прогноза 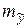 :
:
 ;
;
б) доверительный интервал прогноза
 .
.
Практические рекомендации по выполнению расчетов
с помощью табличного редактора MS Excel
Активизация надстройки Пакет анализа
Для активизации надстройки Пакет анализа необходимо выполнить следующие действия:
1. Выбрать команду Сервис/Надстройки.
2. В появившемся диалоговом окне установить флажок Пакет анализа.

В соответствии с вариантом задания, используя статистический материал, необходимо:
1. Рассчитать параметры уравнения линейной парной регрессии 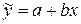 .
.
2. Оценить тесноту связи зависимой переменной (результативного фактора) с объясняющей переменной с помощью показателей корреляции и детерминации.
3. Оценить с помощью F -критерия Фишера статистическую надежность моделирования.
4. Оценить статистическую значимость параметров регрессии.
5. Определить среднюю ошибку аппроксимации.
6. Используя коэффициент эластичности, выполнить количественную оценку влияния объясняющего фактора на результат.
7. Выполнить точечный и интервальный прогноз результативного признака y при увеличении объясняющего признака x на 25% от его среднего значения (достоверность прогноза 95%).
8. На одной диаграмме изобразить поле корреляции исходных данных и прямую регрессии.
Пример
Имеются данные о годовой цене программы «Мастер делового администрирования» и числе слушателей в образовательном учреждении.
| Цена программы, тыс. долл., y | 4,9 | 3,8 | 3,5 | 3,8 | 3,7 | 3,6 | 3,5 | 3,4 | |||||
| Число слушателей, чел., x |
I. Вводим исходные данные в документ Excel.
II. Значения фактора x должны быть отсортированы по возрастанию с сохранением соответствующего значения y. Это может быть сделано так Данные/Сортировка/ Выделить столбец, в котором необходимо сделать сортировку. Например,

III. Вызываем надстройку Анализ данных в меню Сервис.
IV. Выбираем инструмент Регрессия.

V. Заполняем соответствующие позиции окна Регрессия.

VI. После нажатия ОK получаем протокол решения задачи.
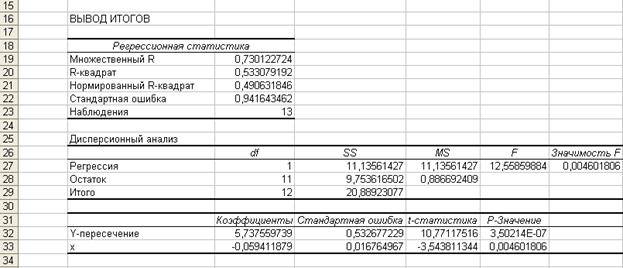
VII. Анализируем полученный протокол.
1) Параметры уравнения линейной парной регрессии 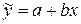 .
.
Коэффициент регрессии 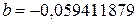 ;
;
Свободный член уравнения регрессии  .
.
Примечание. При необходимости результаты округляются с нужной точностью. Требование по округлению можно провести изначально, задав количество знаков после запятой в меню Формат ячейки.
Уравнение парной линейной регрессии имеет вид: 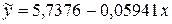 .
.
2) Оцениваем тесноту связи зависимой переменной (результативного фактора) с объясняющей переменной с помощью показателей корреляции и детерминации.
Коэффициент корреляции  , что свидетельствует о тесной связи признаков y и x. Коэффициент детерминации
, что свидетельствует о тесной связи признаков y и x. Коэффициент детерминации 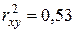 . Полученное уравнение регрессии объясняет 53% вариации признака y, остальные 47% изменчивости этого признака обусловлены влиянием неучтенных в модели факторов.
. Полученное уравнение регрессии объясняет 53% вариации признака y, остальные 47% изменчивости этого признака обусловлены влиянием неучтенных в модели факторов.
3) Оцениваем с помощью F -критерия Фишера статистическую надежность моделирования.
Расчетное значение критерия Фишера указано в протоколе, 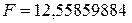 . Критическое значение этого критерия можно найти с помощь статистической функции FРАСПОБР табличного редактора Еxcel.
. Критическое значение этого критерия можно найти с помощь статистической функции FРАСПОБР табличного редактора Еxcel.
Входными параметрами этой функции являются:
– уровень значимости (вероятность), имеется в виду вероятность ошибки отвергнуть верную гипотезу о статистической незначимости построенного уравнения регрессии. Как правило, выбирают уровень значимости, равный 0,05 или 0,01;
– число степеней свободы 1 – совпадает с количеством параметров при переменной x в уравнении регрессии, для парной линейной регрессии 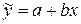 это число равно единице;
это число равно единице;
– число степеней свободы 2 равно для парной линейной регрессии 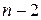 , где n – объем исходных статистических данных.
, где n – объем исходных статистических данных.
Выполняем действия Вставка/Функция, выбираем нужное.
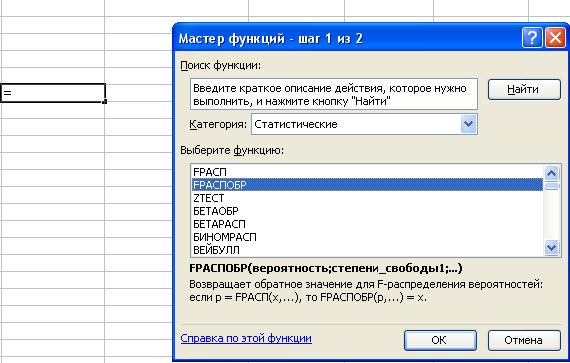
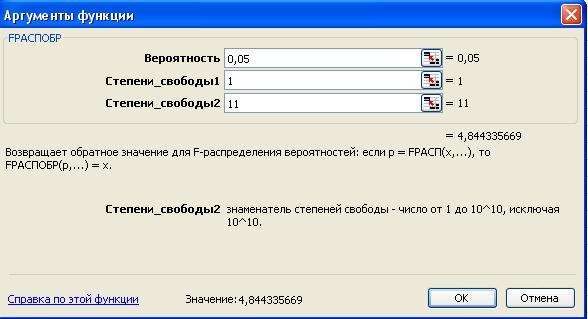
Вывод: поскольку расчетное значение F-критерия больше критического, равного 4,84, нулевая гипотеза об отсутствии значимой связи признаков x и y отклоняется и делается вывод о существенности этой связи.
4) Оценить статистическую значимость параметров регрессии.
Оценим статистическую значимость параметров a и b в уравнении регрессии с помощью t - критерия Стьюдента.
Расчетные значения статистики Стьюдента берем из протокола (графа t -статистика): 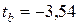 ,
, 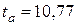 . Соответствующее критическое значение можно определить через статистическую функцию СТЬЮДРАСПОБР, число степеней свободы равно
. Соответствующее критическое значение можно определить через статистическую функцию СТЬЮДРАСПОБР, число степеней свободы равно 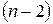 .
.
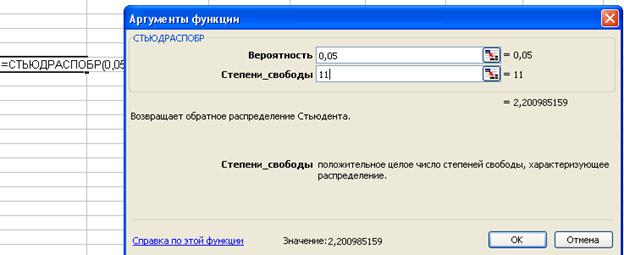
Вывод: поскольку фактические значения по абсолютной величине превышают табличное, равное 2,2, гипотезу о несущественности параметров регрессии можно отклонить.
5) Определяем среднюю ошибку аппроксимации.
Вычисляем среднюю ошибку аппроксимации,  . Понадобится выполнение вспомогательных расчетов, оформленных в виде таблицы.
. Понадобится выполнение вспомогательных расчетов, оформленных в виде таблицы.
| y | x | 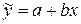
| 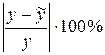
| |
| 5,440500341 | 31,99374573 | |||
| 5,143440944 | 2,868818882 | |||
| 4,9 | 5,024617185 | 2,543207862 | ||
| 4,846381547 | 21,15953867 | |||
| 3,8 | 4,54932215 | 19,71900394 | ||
| 3,5 | 4,430498391 | 26,58566831 | ||
| 3,8 | 4,252262752 | 11,90165138 | ||
| 3,7 | 3,955203355 | 6,897387976 | ||
| 3,6 | 3,658143958 | 1,615109941 | ||
| 3,5 | 3,598732078 | 2,820916526 | ||
| 3,4 | 3,361084561 | 1,144571747 | ||
| 2,766965766 | 7,767807796 | |||
| 2,172846972 | 27,57176761 | |||
| Среднее | 4,092307692 | 27,69230769 | 12,66070741 |
Вывод: средняя ошибка аппроксимации по данному уравнению регрессии составляет 12,66%, модель парной линейной регрессии можно признать удовлетворительной и пригодной для прогнозирования.
6) Используя коэффициент эластичности, выполним количественную оценку влияния объясняющего фактора на результат.
Для парной линейной регрессии эластичность можно найти по формуле  . Имеем
. Имеем
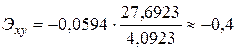 .
.
Следовательно, при увеличении количества слушателей на 1% годовая цена уменьшится на 0,4%.
7) Выполним расчет прогноза y при увеличении фактора x на 25% от своего среднего значения.
Среднее значение  (чел).
(чел).
Прогнозное значение 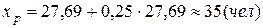 .
.
Точечный прогноз признака y вычисляем по построенному уравнению линейной регрессии: 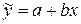 ,
, 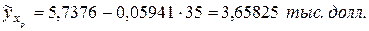 .
.
Среднюю ошибку прогноза вычисляем по формуле 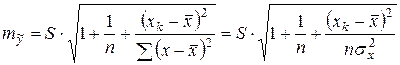 ,
,
где  – остаточная дисперсия,
– остаточная дисперсия, 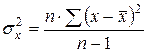 –дисперсия фактора x.
–дисперсия фактора x.
Численное значение суммы 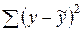 в протоколе обозначено как остаточное SS.
в протоколе обозначено как остаточное SS.

Тогда 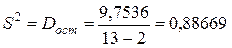 ,
, 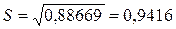 .
.
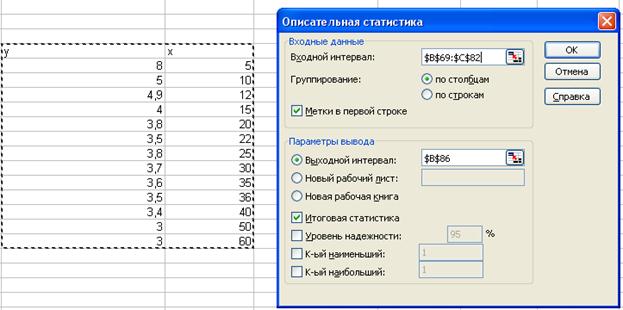
Самый быстрый способ получения вспомогательных характеристик  – среднего значения фактора x и
– среднего значения фактора x и 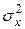 - дисперсии, воспользоваться инструментом Описательная статистика в пакете Анализ данных.
- дисперсии, воспользоваться инструментом Описательная статистика в пакете Анализ данных.
Протокол вывода результатов имеет вид
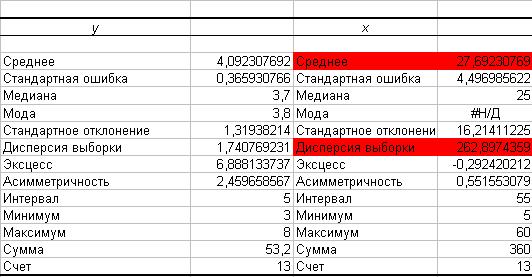
Имеем 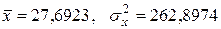 .
.
Тогда  .
.
Доверительный интервал прогноза:  , где
, где  –критическое значение критерия Стьюдента (найдено ранее по функции СТЬЮДРАСПОБР,
–критическое значение критерия Стьюдента (найдено ранее по функции СТЬЮДРАСПОБР, 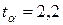 при уровне значимости
при уровне значимости 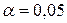 ).
).
Следовательно,
 ;
;
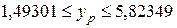 ,
,
т.е. можно быть уверенным на 95%, что цена годового курса при 35 слушателях будет варьироваться в указанных пределах (при точечном прогнозе цены в 3,65825 тыс. долл.).
8) Для построения диаграммы выполним следующие действия:
Шаг 1 Вставка/ Диаграмма/График
Шаг 2 Далее/Диапазон/ Выделить столбец исходных значений фактора y

Шаг 3 Ряд/Добавить/Значения/ Выделить столбец регрессионных значений фактора –  .
.
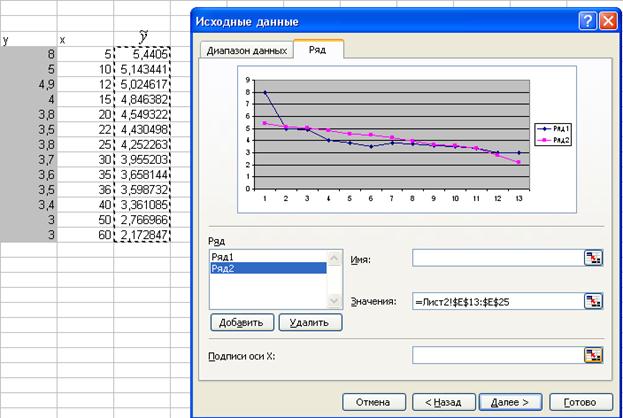
Шаг 4 Подписи оси X / Выделить столбец значений x.
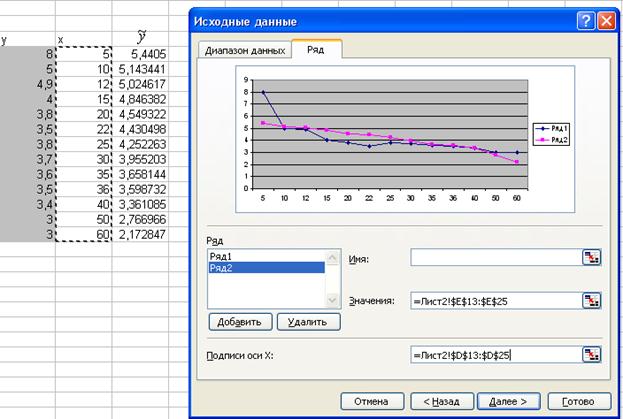
Шаг 5 Каждому из рядов присвоить имя, подписать оси координат и название диаграммы.
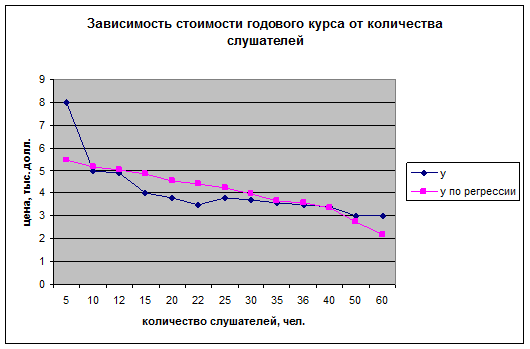
Задания для самостоятельной работы
Вариант 1
x – энерговооруженность на 10-ти предприятиях, кВт;
y – производительность труда, тыс. руб.
| x | 2,8 | 2,2 | 3,5 | 3,2 | 3,7 | 4,8 | 5,4 | |||
| y | 6,7 | 6,9 | 7,2 | 7,3 | 8,4 | 8,8 | 9,1 | 9,8 | 10,6 | 10,7 |
Вариант 2
x – энерговооруженность на 10-ти предприятиях, кВт;
y – производительность труда, тыс. руб.
| x | 3,2 | 3,7 | 4,8 | 5,4 | 5,2 | 5,4 | ||||
| y | 8,4 | 8,8 | 9,1 | 9,8 | 10,6 | 10,7 | 11,1 | 11,8 | 12,1 | 12,4 |
Вариант 3
x – качество земли, баллы;
y – урожайность, ц/га.
| x | ||||||||||
| y | 19,5 | 20,5 | 20,8 | 21,4 | 23,3 | 24,5 |
Вариант 4
x – качество земли, баллы;
y – урожайность, ц/га.
| x | ||||||||||
| y | 24,2 | 26,8 | 27,2 | 30,2 |
Вариант 5
x – товарооборот;
y –издержки обращения по отношению к товарообороту.
| x | ||||||||
| y | 7,5 | 6,3 | 5,8 | 5,4 |
Вариант 6
x – электровооруженность на одного рабочего;
y – выпуск готовой продукции на одного рабочего.
| x | ||||||||||
| y |
Вариант 7
x –уровень доходов семьи;
y – расходы на продукты питания (в расчете на 100 руб. доходов).
| x | 1,4 | 3,3 | 5,5 | 7,6 | 9,8 | 14,7 | 18,9 | |
| y | 1,1 | 1,4 | 2,4 | 2,8 | 3,1 | 3,5 |
Вариант 8
x – качество земли, баллы;
y – урожайность, ц/га.
| x | ||||||||
| y | 23,3 | 24,5 | 24,2 |
Вариант 9
x – производительность труда;
y – рентабельность производства.
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| y | 2,6 | 2,4 | 3,3 | 2,9 | 3,7 | 4,2 | 5,5 | 6,4 |
Вариант 10
x – производительность труда;
y – рентабельность производства.
Поиск по сайту: