 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 3. Системы. Модели систем
Первое определение системы. Многообразие реальных систем. Общее и частное (специальное) в содержании и структуре социально-экономических систем и бизнес-процессов. Модели систем: модель «черного ящика»; модель состава системы; модель структуры системы – «белый ящик». Статистические и динамические модели систем. Время в задачах моделирования. Формальность и содержательность моделей. Искусство создания моделей систем. Второе определение системы. Структурная схема системы.

Рис. 3.1.
Упрощенные примеры уже существующих систем, предназначенных для реализации определенных целей указаны в табл.3.1. (7,8,9 заполнить самостоятельно)
Таблица 3.1
| № | Цель | Система |
| 1. | В любой момент указать время | Часы |
| 2. | Обеспечить выпечку хлеба в заданном ассортименте и количестве для потребителей | Пекарня |
| 3. | Обеспечить продажу товаров в заданном ассортименте и количестве для потребителей | Магазин |
| 4. | Передать звуковую информацию на большие расстояния практически мгновенно | Радио |
| 5. | Передать зрительную информацию в звуковом сопровождении на большие расстояния практически мгновенно | Телевидение |
| 6. | Обеспечить потребности в быстром перемещении людей в пределах города | Городской транспорт |
| 7. | ||
| 8. | ||
| 9. |
| |||||||
 | |||||||
|
| ||||||

Рис.3.2. Модель черного ящика
Таблица 3.2
| Система | Подсистемы | Элементы |
| 1. Система телевидения “Орбита” | Подсистема передачи | Центральная телестудия Антенно-передающий центр |
| Канал связи | Среда распространения радиоволн Спутники-рентрансляторы | |
| Приемная подсистема | Местные телевизоры Телевизоры потребителей | |
| 2. Семья | Члены семьи | Муж. Жена. Предки. Потомки. Другие родственники |
| Имущество семьи | Общая собственность (жилье, хозяйство, бизнес) Личная собственность членов семьи | |
| 3. Отопительная система дома | Источники тепла | Котельная, бойелерная, отвод от центральной теплотрассы |
| Подсистема доставки и распределения тепла | Трубы. Калориферы. Вентили | |
| Подсистема эксплуатации | Службы эксплуатации и ремонта. Персонал | |
| 4. | ||
| 5. | ||
| 6. | ||
| 7. |
 | |||
 | |||
|


|



|


|
|
|



|
| |||||||||||||||||||
 | |||||||||||||||||||
 |  | ||||||||||||||||||
 | |||||||||||||||||||
| |||||||||||||||||||
 |  | ||||||||||||||||||
 | |||||||||||||||||||
| |||||||||||||||||||
 | |||||||||||||||||||
Рис.3.3. Модель состава системы
Таблица 3.3. Структура системы "часы"
| Пара элементов | Связь между ними |
| Датчик и индикатор | Однозначное соответствие |
| Эталон и датчик | Приблизительное соответствие |
| Индикатор и эталон | Периодическое сравнение и устранение расхождения |
 Например, Е – множество. Любое свойство, которым может обладать элемент х Î Е, задает в Е подмножество А Í Е всех элементов, обладающих этим свойством. Пусть задано некоторое отношение R, в котором могут находиться элементы х и у множества Е, записанные в указанном порядке. Если они находятся в заданном отношении, то используется запись xRy, если нет то запись xRy. Множество всех упорядоченных пар (х,у) (т.е. (х,у) и (у,х) – разные пары при х ¹ у) называется произведением Е ´ Е. Рассмотрим подмножество R Í Е´ Е всех пар, для которых xRy. Задание этого подмножества и является заданием отношения. Если теперь ввести понятие многоместного (а не только двуместного, бинарного) отношения, то свойство оказывается одноместным (унарным) отношением.
Например, Е – множество. Любое свойство, которым может обладать элемент х Î Е, задает в Е подмножество А Í Е всех элементов, обладающих этим свойством. Пусть задано некоторое отношение R, в котором могут находиться элементы х и у множества Е, записанные в указанном порядке. Если они находятся в заданном отношении, то используется запись xRy, если нет то запись xRy. Множество всех упорядоченных пар (х,у) (т.е. (х,у) и (у,х) – разные пары при х ¹ у) называется произведением Е ´ Е. Рассмотрим подмножество R Í Е´ Е всех пар, для которых xRy. Задание этого подмножества и является заданием отношения. Если теперь ввести понятие многоместного (а не только двуместного, бинарного) отношения, то свойство оказывается одноместным (унарным) отношением.
Например, в структурной схеме системы “синхронизируемые часы” (рис.3.4) элементы изображены в виде прямоугольников; связи 1-3 в таб. 3.3; вход 4 изображает поступление энергии из вне; вход 5 соответствует регулировке индикатора; выход 6 показание часов.
 | |||
|
 |



 Рис. 3.5. Пример графа
Рис. 3.5. Пример графа

Рис. 3.6. Графы, соответствующие различным структурам: а) линейная; б) древовидная (иерархическая); в) матричная; г) сетевая (в технических системах); д) с обратными связями (кольцевые пути в ориентированных графах)
Типы динамических моделей. При математическом моделировании процесса его конкретная реализация описывается в виде соответствия между элементами множества Х возможных “значений” х и элементов упорядоченного множества Т “моментов времени” t, т.е. в виде отображения Т Õ Х: х(t) Î Х, t Î Т. С помощью этих понятий можно строить математические модели систем.
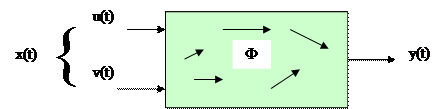 |
Рис. 3.7. Динамическая модель “черного ящика”: задание процессов на входах и выходах системы
Рассматривая выход у(t) системы (это может быть вектор) как ее реакцию на управляемые u(t) и неуправляемые v(t) входы х(t) = {u(t), v(t)} (рис. 3.7), можно модель “черного ящика” выразить как совокупность двух процессов: Х = {х(t)} и Y = {y(t)}, t Î Т. Если даже считать у(t) результатом некоторого преобразования Ф процесса х(t), т.е. у(t) = Ф(х(t)), то модель «черного ящика» предполагает, что это преобразование неизвестно. В случае «белого ящика», соответствие между входом и выходом можно описать тем или иным способом, который зависит от того, что нам известно, и в какой форме можно использовать эти знания.
Например, иногда известно, что система мгновенно преобразует вход в выход, т.е. у(t) является функцией только х(t) в тот же момент времени. Остается задать или найти эту функцию. На практике чаще известна лишь безинерционность системы и требуется, наблюдая входы и выходы, восстановить неизвестную функцию у = Ф(х). По существу, это задача о переходе от модели «черного ящика» к модели «белого ящика» по наблюдениям входов и выходов при наличии информации о безинерционности системы. Даже в такой достаточно простой постановке задача имеет совсем не простые варианты, которые зависят от того, что известно о функции Ф (в параметризованном случае Ф принадлежит семейству функций, известных с точностью до параметров; в непараметризованном – вид функции Ф неизвестен), и от наличия или отсутствия некоторых общих сведений о ее свойствах (непрерывности, гладкости, монотонности, симметричности и т.п.).
Дополнительные варианты (и дополнительные трудности) возникают, если входы или выходы наблюдаются с помехами или искажениями. При этом разные предположения о природе этих помех приводят к принципиально отличающимся решениям задачи (например, в случае, когда распределение помехи известно точно, с точностью до числовых параметров или неизвестно совсем). Однако класс систем, которые условно безинерционные весьма узок, а необходимо в модели отразить и возможные изменения.
В общей математической модели динамики это достигается введением понятия состояния системы как некоторой внутренней характеристики системы, значение которой в настоящий момент времени определяет текущее значение выходной величины. Состояние можно рассматривать как хранилище информации, необходимой для предсказания влияния настоящего на будущее. Обозначим это состояние через z(t). Все сказанное выше означает существование такого отображения h: Z ´ T ® Y, что
y(t) = h(t,z(t)), t Î T. (3.1)
Явная зависимость h от t введена для учета возможности изменения зависимости выхода от состояния с течением времени. Это отображение называется отображением выхода. Для завершения построения модели нужно описать связь между входом и состоянием, т.е. ввести параметрическое семейство отображений mtt: Z ´ Х (.) ® Z, заданных для всех значений параметров t Î Т, t Î Т и t £ t. Это означает принятие аксиомы о том, что состояние в любой момент t > t однозначно определяется состоянием Zt в момент t и отрезком реализации входа х(.) от t до t:
z(t) = mtt(zt,х(.)) = d (t,t,zt,x(.)). (3.2)
Такое отображение называют переходным отображением. Итак, математическая модель системы, соответствующая уровню “белого ящика”, - это задание множества входов, состояний и выходов, связей между ними:
D h
Х ® Z ® Y. (3.3)
Конкретизируя множества Х, Z и Y и отображая d и h, можно перейти к моделям различных систем. Так, говорят дискретных и непрерывных по времени системах, в зависимости от того, дискретно или непрерывно множество Т. Далее, если множества Х, Z, Y дискретной по времени системы имеют конечное число элементов, то такую систему называют конечным автоматом. Это относительно простой класс систем, поскольку для исследования конечных автоматов необходимы лишь методы логики и алгебры; в то же время это практически важный класс, так как в него входят все дискретные (цифровые) измерительные, управляющие и вычислительные устройства, в том числе и ЭВМ.
Если Х, Z, Y – линейные пространства, а d и h - линейные операторы, то и система называется линейной. Если к линейной системе дополнительно предъявить требования, состоящие в том, чтобы пространства имели топологическую структуру, а d и h были непрерывны в этой типологии, то мы приходим к гладким системам. Этот класс систем имеет большое значение, поскольку оказалось, что для гладких систем переходное отображение d является общим решением дифференциального уравнения
|
(3.4)
а для дискретных систем – общим решением уравнения
Z(tk+1) = f (tk,z,x) = d(tk+1; tk, z, x(.)), (3.5)
Где х (.) - траектория для моментов времени t £ tk.
Интенсивно исследовались стационарные системы, свойства которых со временем не изменяются. Стационарность означает независимость от t функции h и инвариантность функции d к сдвигу во времени:
h (t, z(t)) = h(z(t)), d(t; to, z x(.)) = d(t + t; to + t, z, x (.)),
где х (.) есть х (.), сдвинутое на время t.
Конкретизация моделей динамических систем на этом не заканчивается, поскольку приведенные модели являются примерами, которые можно рассматривать отдельно. Но на одном свойстве реальных динамических систем следует остановиться – на принципе причинности, согласно которому отклик системы на некоторое воздействие не может начаться раньше самого воздействия. Это условие, очевидное для реальных систем, совсем не автоматически выполняется в рамках их математических моделей. В связи с этим одна из проблем теории динамических систем состоит в выяснении условий физической реализуемости теоретических моделей, т.е. конкретных ограничений, которые приходится накладывать на модель при соблюдении принципа причинности.
| “Черный ящик” | Состав | Структура | Структурная схема |
                                                         
|
а)
| “Черный ящик” | Состав | Структура | Структурная схема |
| Вход: начальное состояние Выход: конечное (желаемое) состояние | Перечень действий, необхо-димых для перевода началь-ного состояния в конечное | Последовательность дейст-вий и продолжительность каждого действия | Сетевой график всего процесса |
б)
Рис. 3.8. Типы моделей: а) статический вариант; б) динамический вариант
Поиск по сайту: