КОЛИЧЕСТВО ИНФОРМАЦИИ

В основе теории информации лежит открытие, что информация допускает количественную оценку. В простейшей формулировке идея эта выдвинута еще в 1928 г. Хартли, но завершенный и общий вид придал ей Шэннон в 1948 г.

КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СНЯТОЙ НЕОПРЕДЕЛЕННОСТИ

Процесс получения информации можно интерпретировать как изменение неопределенности в результате приема сигнала. Проиллюстрируем эту идею на примере достаточно простого случая, когда передача сигнала происходит при следующих условиях:

1) полезный (отправляемый) сигнал является последовательностью статистически независимых символов с вероятностями р(х;), i = ;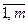

2) принимаемый сигнал является последовательностью символов у того же алфавита;

3) если шумы (искажения) отсутствуют, то принимаемый сигнал совпадает с отправляемым у = х ;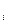

4) если шум имеется, то его действие приводит к тому, что данный символ может быть либо остаться прежним (i-м), либо быть подмененным любым другим (k -м) символом, вероятность этого равна р(у | х );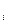

5) искажение очередного символа является событием, статистически независимым от того, что произошло с предыдущими символами.

Итак, до получения очередного символа ситуация характеризуется неопределенностью того, какой символ будет отправлен, т.е. априорной энтропией Н(Х). После получения символа у неопределенность относительно того, какой символ был отправлен, меняется: в случае отсутствия она вообще исчезает, а при наличии шума мы не можем быть уверены, что полученный нами символ и есть отправленный, и возникает неопределенность, характеризуемая апостериорной энтропией Н(Х| у ) = H() > О. В среднем после получения очередного символа энтропия Н(Х|Y) = M H(X|у )

Определим теперь количество информации как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропий этого объекта.

КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СООТВЕТСТВИЯ СЛУЧАЙНЫХ ОБЪЕКТОВ

(1)

Эта формула означает, что количество информации в объекте Х об объекте Y равно количеству информации в объекте Y об объекте Х. Таким образом, количество информации является не характеристикой одного из объектов, а характеристикой их связи, соответствия между их состояниями. Подчеркивая это, можно сформулировать еще одно определение: среднее количество информации, вычисляемое по формуле (1), есть мера соответствия двух случайных объектов.

Это определение позволяет прояснить связь понятий информации и количества информации. Информация есть отражение одного объекта другим, проявляющееся в соответствии их состояний. Один объект может быть отражен с помощью нескольких других, часто какими-то лучше, чем остальными. Среднее количество информации и есть числовая характеристика степени отражения, степени соответствия. Подчеркнем, что при таком описании как отражаемый, так и отражающий объекты выступают совершенно равноправно. С одной стороны, это подчеркивает обоюдность отражения: каждый из них содержит информацию друг о друге. Это представляется естественным, поскольку отражение есть результат взаимодействия, т.е. взаимного, обоюдного изменения состояний. С другой стороны, фактически одно явление (или объект) всегда выступает как причина, другой — как следствие; это никак не учитывается при введенном количественном описании информации.

СВОЙСТВА КОЛИЧЕСТВА ИНФОРМАЦИИ

Отметим некоторые важные свойства количества информации.

1 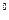. Количество информации в случайном объекте Х относительно объекта Y равно количеству информации в Y относительно Х:

I(X, Y) =I(Y, Х). (2)

2 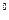. Количество информации неотрицательно:

I(X, Y) 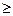О. (3)

3 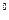. Для дискретных Х справедливо равенство I(X,X) = Н(Х).

4 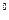. Преобразование одной случайной величины не может увеличить содержание в ней информации о другой, связанной с ней, величине:

I ( (X),Y) I(X,Y). (4)

5 . Для независимых пар величин количество информации аддитивно:

I () = (5)

ЕДИНИЦЫ ИЗМЕРЕНИЯ ЭНТРОПИИ И КОЛИЧЕСТВА ИНФОРМАЦИИ

Рассмотрим теперь вопрос о единицах измерения количества информации и энтропии. Из определений I и Н следует их безразмерность, а из линейности их связи — одинаковость их единиц. Поэтому будем для определенности говорить об энтропии. Начнем с дискретного случая. За единицу энтропии примем неопределенность случайного объекта, такого, что

Н (Х) = - . (6)

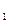Легко установить, что для однозначного определения единицы измерения энтропии необходимо конкретизировать число состояний объекта и основание логарифма. Возьмем для определенности наименьшее число возможных состояний, при котором объект еще остается случайным, т.е. = 2, и в качестве основания логарифма также возьмем число 2. Тогда из равенства вытекает, что р = р 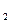= 1/2. Следовательно, единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Эта единица получила название "бит". Бросание монеты дает количество информации в один бит. Другая единица ("нит") получается, если использовать натуральные логарифмы, обычно она употребляется для непрерывных величин.

Поиск по сайту: