ЯЗЫК БИНАРНЫХ ОТНОШЕНИЙ

Рис. 7.4.2.

В реальности дать оценку отдельно взятой альтернативе часто затруднительно или невозможно; однако если рассматривать ее не в отдельности, а в паре с другой альтер­нативой, то находятся основания сказать, какая из них более предпочти­тельна.

Таким образом, основные предположения этого языка сводятся к следующему:

1) отдельная альтернатива не оценивается, т.е. критериальная функ­ция не вводится;

2) для каждой пары альтернатив (х, у) некоторым образом можно установить, что одна из них предпочтительнее другой либо они равноценны или несравнимы (чаще всего последние два понятия отождеств­ляются);

3) отношение предпочтения внутри любой пары альтернатив не зависит от остальных альтернатив, предъявленных к выбору.

Математически бинарное отношение R на множестве X определяется как определенное подмножество упорядоченных пар (х, у). Удобно; использовать обозначение xRy, если х находится в отношении R с у, и x y в противном случае. Множество всех пар {(х, у), х,

у } называется полным ("универсальным") бинарным отношением. Поскольку в общем случае не все возможные пары (х, у) удовлетворяют условиям, накладываемым отношением R, бинарное отношение является некоторым подмножеством полного бинарного отношения, т.е. .

Задать отношение — это значит тем или иным способом указать всепары (х, у), для которых выполнено отношение R.

Существует четыре разных способа задания отношений (рис. 7.4.2.); преимущества каждого проявляются при разных характеристиках множества X.

Первый, очевидный, способ состоит в непосредственном перечисле­нии таких пар. Ясно, что он приемлем лишь в случае конечного мно­жества X.

Второй удобный способ задания отношения R на конечном множестве — матричный. Все элементы нумеруются, и матрица отношения R определяется своими элементами a_ij(R) = {l: x_jRх_j; 0: x_i x_j } для всех i и j. Известным примером такого задания отношений являются турнирные таблицы (если ничьи обозначить нулями, как и проигрыш, то матрица изобразит отношение «х_i — победитель x_j»).

Третий способ - задание отношения графом. Вершинам графа G(R) ставят в соответствие (пронумерованные) элементы множества X, и если x_iRx_j, тоот вершины х_i проводят направленную дугу к вершине x_j; если же x_i x_j, то дуга отсутствует.

Для определения отношений на бесконечных множествах исполь­зуется четвертый способ - задание отношения R сечениями. Множество:

называется верхним сечением отношения, а множество:

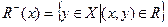
— нижним сечением.

Для теории выбора особое значение среди всех бинарных отношений имеют отношения, которые соответствуют предпочтению одной альтер­нативы перед другой или случаю невозможности отдать предпочтение одной из двух альтернатив. Эти отношения можно задать через строго определяемые отношения эквивалентности, порядка и доминирования

Бинарное отношение R на множестве X называется:

• рефлексивным, если xRx для каждого ;
• антирефлексивным, если х (т.е. R может выполняться только для несовпадаю­щих элементов);
• симметричным, если xRy ;
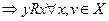• асимметричным, если хRу 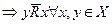( ясно, что асимметричное отношение R анти­рефлексивно);
• антисимметричным, если для всех х, 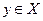(xRy, yRx) => х = у;
• транзитивным, если для всех х, у, (xRy, yRz) => xRz;
• отрицательно транзитивным, если отноше­ние транзитивно;
• сильно транзитивным, если отношение R одновременно транзитивно и отрицательно транзитивно.

Очень важное предположение в языке бинарных отношений — независимость упорядочения двух альтернатив от любой третьей. Это предположение существенно для всей теории. В ее приложениях важно убедиться, что оно выполняется в изучаемом варианте выбора.

Отношение R на множестве X называется отношением эквивалентности (обозначение ~), если оно рефлексивно, симметрично и транзитивно. Примеры отношений эквивалентности: "быть четным", "иметь одинаковый остаток от деления на 3" — на множестве натуральных чисел; "быть одноклассниками" - на множе­стве учеников данной школы; "быть подобными" — на множестве многоугольников. Задание отношения эквивалентности равносильно разбиению множества X на непересекающиеся классы () эквивалентных элементов: х ~ у тогда и только тогда, когда х, у 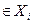(т.е. если х и у принадлежат одному классу эквивалентности).

Отношением нестрогого порядка (обозначение ) называется реф­лексивное, антисимметричное и транзитивное отношение. Отношением строгого порядка (обозначение <) называется антирефлексивное, асим­метричное и транзитивное отношение. Отношение нестрогого порядка можно рассматривать как объединение отношений < и ~.

Наконец, отношением доминирования называется отношение, обла­дающее антирефлексивностью и асимметричностью. Говорят, что "х доминирует у" (обозначается х >> у), когда х в каком-то смысле превос­ходит у. (Очевидно, строгий порядок — частный случай доминирования, при котором имеет место еще транзитивность.)

В случае конечных множеств X очень удобно находить наилучшие альтернативы с помощью графа предпочтений, стрелки которого направ­лены в сторону менее предпочтимой альтернативы

Несмотря на то, что язык бинарных отношений введен для описания более общих и сложных ситуаций, нежели те, которые описываются критериальным языком, в чисто познавательных целях поучительно просле­дить, как уже известная нам ситуация выглядит в новом представлении. Например, многомерное критериальное пространство может быть поставлено в соответствие евкли­дову пространству. Введение на этом пространстве бинарных отноше­ний требует учета его свойств. В частности, начинают играть роль отно­шения инвариантные (относительно переноса), для которых верхнее сечение в любой точке может быть получено параллельным переносом верхнего сечения в любой другой точке.

Рис. 7.4.3. Описание паретовского множества как множества таких альтернатив, для которых верхнее сечение Р⁺ _(x) пусто

Примером инвариантного отношения является отношение Парето Р:

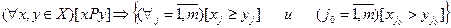
Верхнее сечение отношения Р есть первый квадрант с началом в точке х;теперь понятно, как находится паретовское множество альтернатив (на рис. 7.4.3. приведен случай конечного множества X; сравните этот рисунок с рис.1, г)):в паретовское множество включаются альтернативы, верхнее сечение которых пусто (на рис. 7.4.3. они отмечены кружками).

В общем же случае выделение наиболее предпочтительных альтернатив возможно с помощью понятия оптимальности по отношению R, позволяющего придавать разный смысл понятию "наилучший" (задавая разные отношения R). Элемент называется мажорантой по отношению R на X, если для всех 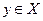выполнено условие y x. Множест­во X₊{R) всех мажорант называется множеством R-оптимальных эле­ментов.

Понятие расплывчатости. Важно обсудить ситуацию, возникшую при описании выбора на язы­ке бинарных отношений в результате создания теории полезности. П. Фишберн строго доказал теорему, смысл которой довольно ясен: если множество X конечно и между его элементами имеется отношение строгого порядка, то можно построить такую вещественную функцию и(х) на X, для которой

(x<y) => [ u(x)<u(y) ]

(в левой части < означает отношение предпочтения, в правой — знак "меньше").

Функция и(х) называется функцией полезности.

Создается впечатление, что от качественных порядковых измере­ний можно перейти к количественным. На самом деле мы здесь вновь сталкиваемся с такой ситуацией, когда "оцифровка" порядковой шкалы не делает ее числовой шкалой. Для воспроизводства упорядочения фиксированного попарно упорядоченного множества X, конечно, можно воспользоваться числовой функцией и(х); однако стоит допол­нить X альтернативами, которые не рассматривались при первом упоря­дочении, как функцию и(х) потребуется определять заново. Более того, если два разных эксперта дадут разные упорядочения множества X, го можно доопределить функции полезности для каждого из них, но сравнивать их численно иначе как в отношении порядка не имеет смысла, хотя обе они определены на одном множестве.

ЯЗЫК ФУНКЦИЙ ВЫБОРА описывает выбор как операцию над произвольным множеством альтернатив X, которая ставит этому множеству в соответствие некоторое его подмножество С(Х): С(Х) X. Главное достоинстве нового языка — возможность рассмотрения более сложных правил выбора. На такую возможность указывает хотя бы различие числа возможных функций выбора и числа возможных графов предпочтения на множестве n альтернатив. Число графов, отличающихся наличием или отсутствием хотя бы одной дуги, равно . Если для выбора предлагаются k из n альтернатив, то число функций выбора равно 2 ^k (каждая из альтернатив может либо входить в C(X_k), либо нет). Так как число возмож­ных вариантов предъявления альтернатив равно 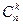, то общее число функций выбора равно . Как видим, разнообразие функций выбора намного превосходит разнообразие графов предпочте­ния. Кроме того, здесь сразу допускается отказ от выбора, т.е. пустой выбор C(X_i) = , что также расширяет множество правил выбора.

Ограничения на функции выбора. Различие между классами правил выбора можно выразить через различные ограничения, которым подчиняется тот или иной тип функ­ции выбора. Приведем некоторые из таких ограничений:

Рис. 7.5. Иллюстрация различных аксиом, накладываемых на функции выбора.

Аксиома наследования (Н):

Смысл этой аксиомы сводится к требованию, чтобы в выбор на под­множестве X' вошли все те альтернативы из X', которые входили в вы­бор на X (возможно, еще и другие; рис. 7.5., а)).

Аксиома согласия (С):

Это означает, что в выбор из объединения множеств обязательно должны входить альтернативы, общие для выборов из всех множеств (и, воз­можно, другие альтернативы; рис. 7.5., б)).

Оказывается, совместное подчинение функции выбора аксиомам Н и С дает выбор, описываемый в языке бинарных отношений.

Аксиома отбрасывания (О):

Это означает, что если отбросить любую часть отвергнутых при выборе альтернатив, то выбор на оставшемся множестве не изменится (рис. 7.5., в)); поэтому данную аксиому называют также условием независимости отвергнутых альтернатив.

Совместное наложение на выбор аксиом Н, С и О приводит к случаю выбора паретовского множества.

Аксиома Плотта (КС):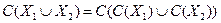

Это отражает требования, накладываемые при многоступенчатых выбоpax, когда считается, например, что определить чемпиона мира можно путем соревнований между чемпионами стран и результат окажется тем же, если соревноваться будут не только чемпионы (рис. 7.5., г)). Поэтому эту аксиому называют еще условием независимости от пути. Функции выбора, удовлетворяющие ей, называются квазисумматорными.

Можно показать, что требование КС эквивалентно совместному выполнению Н и О; следовательно, соединение требований КС и С тоже приводит к паретовскому выбору.

Аксиома предпочтения (П):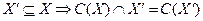

Она требует, чтобы при сужении множества альтернатив в выборе оставались только те альтернативы, которые входили в выбор ранее (рис. 7.5., д)).

Ясно, что некоторые из введенных аксиом можно ослаблять или усиливать (например, П есть усиление Н). Аксиому Плотта можно усилить аксиомы сумматорности:

можно накладывать новые, независимые требования (например, аксиома мультипликаторности: ,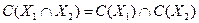

аксиома монотонности:

(рис. 7.5., е)), получая при этом различные типы выбора. Наоборот, можно, изучив ограничения того или иного реаль­ного правила выбора, искать свойства класса функций выбора, удовлет­воряющего этим ограничениям (попробуйте, например, установить, ка­ким аксиомам отвечает и противоречит правило определения победи­теля шахматного турнира по числу набранных очков).

Язык функций выбора является весь­ма общим и потенциально может опи­сать любой выбор. Однако его теория находится в начальной стадии развития и пока еще занимается преимущественно описанием старых ситуаций в новых тер­минах.

Рис. 7.6.Процедура достижения консенсуса

Рис.7.7.

Поиск по сайту: