ОБ ОСНОВНЫХ РЕЗУЛЬТАТАХ ТЕОРИИ ИНФОРМАЦИИ

ИЗБЫТОЧНОСТЬ

Одной из важнейших характеристик сигнала является содержащееся в нем количество информации. Однако по ряду причин количество информации, которое несет сигнал, обычно меньше, чем то, которое он мог бы нести по своей физической природе; информационная нагрузка на каждый элемент сигнала меньше той, которую элемент способен нести. Для описания этого свойства сигналов введено понятие избыточности и определена ее количественная мера.

Пусть сигнал длиной в n символов содержит количество информации I. Если это представление информации обладает избыточностью, то такое же количество информации I может быть представлено с помощью меньшего числа символов. Обозначим через наименьшее число символов, необходимое для представления I без потерь. На каждый символ в первом случае приходится I 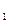= I/n бит информации, во втором бит. Очевидно, . В качестве меры избыточности R принимается относительное удлинение сигнала, соответствующее

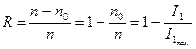. (1)

В дискретном случае имеются две причины избыточности: неравновероятность символов и наличие статистической связи между символами. В непрерывном случае — это неэкстремальность распределений (т.е. отклонение от распределений, обладающих максимальной энтропией), что в широком смысле сводится к отклонениям от экстремальности распределения первого порядка и от минимальности связи во времени (от равномерности спектра при его ограниченности).

Не следует думать, что избыточность — явление всегда отрицательное. При искажениях, выпадениях и вставках символов именно избыточность позволяет обнаружить и исправить ошибки.

СКОРОСТЪ ПЕРЕДАЧИ И ПРОПУСКНАЯ СПОСОБНОСТЪ

Следующим важнейшим понятием является скорость передачи информации. Так называется количество информации, передаваемое в единицу времени. Эта величина определяется по формуле

R=H(X)-H(X|Y), (2)

где указанные энтропии исчисляются на единицу времени. В дискретном случае единицей времени удобно считать время передачи одного символа, тогда в формуле (2) фигурируют априорная и апостериорная энтропии на один символ. Для непрерывных каналов единицей времени может служить либо обычная единица (например, секунда), либо интервал между отсчетами; тогда в формулу (2) входят соответствующие дифференциальные энтропии. Для более наглядного представления о величине R укажем, что темп обычной речи соответствует скорости порядка 20 бит/с, муравьи обмениваются информацией путем касания усиками со скоростью около 1/10 бит/с.

Скорость передачи информации по каналу связи зависит от многих факторов — от энергии сигнала, числа символов в алфавите избыточности, полосы частот, способа кодирования и декодирования. Если имеется возможность изменять некоторые из них, то, естественно, следует делать это так, чтобы максимально увеличить скорость. Оказывается, что обычно существует предел, выше которого увеличение скорости невозможно. Этот предел называется пропускной способностью канала:

С = , (3)

где R — скорость передачи информации при условиях А, {A} — множество вариантов условий, подлежащих перебору. Так как множество {A} можно определить по-разному, то имеет смысл говорить о нескольких типах пропускных способностей. Наиболее важным является случай, когда мощность сигнала (объем алфавита) фиксирована, а варьировать можно только способ кодирования. Именно таким образом пропускную способность определил К. Шэннон. С другой стороны, В.И. Сифоров показал, что целесообразно рассмотреть предел, к которому стремится шэнноновская пропускная способность С при стремлении мощности полезного сигнала к бесконечности. Оказалось, что все каналы связи разбиваются на два класса: каналы первого рода (терминология Сифорова), для которых указанный предел бесконечен, и каналы второго рода, имеющие конечную пропускную способность даже при бесконечной мощности передатчика. Этот предел называют собственной пропускной способностью. При других требованиях, предъявляемых к множеству {A}, мы придем к тем или иным условным пропускным способностям.

Для представления о порядках величин С приведем примеры. Прямыми измерениями установлено, что пропускные способности зрительного, слухового и тактильного каналов связи человека имеют порядок 50 бит/с (вопреки распространенному мнению о сильном отличии зрительного канала). Возможно, ограничивающим фактором являются не сами рецепторы, а нервные волокна, передающие возбуждения. Если включить в канал и "исполнительные" органы человека (например, предложить ему нажимать педаль или кнопку в темпе получения сигналов), то пропускная способность близка к 10 бит/с. Интересно отметить, что многие бытовые технические устройства слабо согласованы с органами чувств человека. Например, канал телевидения имеет пропускную способность в десятки миллионов бит/с.

КОДИРОВАНИЕ В ОТСУТСТВИЕ ШУМОВ

Пусть алфавит системы состоит из т символов. Средствами этого алфавита требуется представить любой из М возможных сигналов , , вероятности которых заданы. Обычно М > m, поэтому каждый из сигналов, подлежащих передаче, невозможно обозначить только одним символом и приходится ставить им в соответствие некоторые последовательности символов; назовем их кодовыми словами. Так как возможна последовательная передача разных кодовых слов, то они не только должны различаться для разных , но и не должны быть продолжением других, более коротких. Пусть сигналу соответствует кодовое слово длиной символов. При стационарной передаче сигналов с вероятностями средняя длина кодового слова равна L = .

Возникает вопрос о том, как выбирать L и . Он не имеет смысла, пока не задан критерий выбора этих величин. Определим этот критерий так: L и должны быть минимальными величинами, такими, при которых еще не происходит потери информации. Напомним, что в отсутствие шумов среднее количество информации на один элемент ансамбля равно энтропии этого ансамбля, т.е. H(U) = , а индивидуальное количество информации в есть . С другой стороны, на один символ придется максимальное количество i информации, если символы равновероятны и независимы; при этом i = log m. Поскольку кодирование должно вестись без потерь информации, сразу получаем

, (4)

, (5)

Так из общих соображений находим нижние границы для L и .

КОДИРОВАНИЕ ПРИ НАЛИЧИИ ШУМОВ

Наиболее интересные и важные результаты были получены при рассмотрении передачи информации по каналам связи с шумами. В этом случае безызбыточное кодирование приведет к безвозвратным потерям информации: искаженный символ нельзя ни обнаружить, ни исправить. Для борьбы с влиянием помех необходимо ввести избыточность в сигнал. Основываясь на интуитивных соображениях (например, на опыте многократного повторения), легко прийти к выводу, что при неограниченном повышении требований к малости вероятности ошибки избыточность и при любом способе кодирования должна неограниченно возрастать, а скорость передачи — стремиться к нулю. Здесь мы имеем яркий пример того, как сильно интуиция может привести к заблуждению. Шэннон показал, что существуют такие способы введения избыточности, при которых обеспечиваются одновременно и сколь угодно малая вероятность ошибки, и конечная (отличная от нуля) скорость передачи информации, причем эта скорость может быть сколь угодно близкой к пропускной способности канала. Это замечательное открытие и привлекло столь большое внимание к теории информации.

ПРОПУСКНАЯ СПОСОБНОСТЬ ГАУССОВА КАНАЛА СВЯЗИ

Гауссовым каналом называется канал связи, для которого выполняются следующие условия:

1) сигналы и шумы в нем непрерывны;

2) канал занимает ограниченную полосу частот шириной F,

3) шум n(t) в канале распределен нормально ("гауссов шум");

4) спектр мощности шума равномерен в полосе частот канала и равен N единиц мощности на единицу полосы частот;

5) средняя мощность полезного сигнала x(t) фиксирована и равна Р ,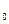

6) сигнал и шум статистически независимы;

7) принимаемый сигнал y(t) есть сумма полезного сигнала и шума:

y(t) =x(t)+ n(t) ("шум аддитивен").

Эти предположения позволяют вычислить пропускную способность гауссова канала. Во-первых, ограниченность полосы частот позволяет применить теорему отсчетов и вести рассуждения для каждого отсчета в отдельности. Далее, аддитивность шума и его независимость от Х позволяют представить количество информации в Y об Х в виде

I(X,Y) = h(Y) – h(Y|X) = h(Y) – h(X+N|X) = h(Y)-h(N), (8)

где h (N) — дифференциальная энтропия шума. Следовательно, пропускная способность такова:

С = .

Согласно условиям 3- 4 имеем

. (9)

В силу условий 4 — 7 мощность принимаемого сигнала есть

. (10)

Максимум h(Y) при условии (10) достигается в случае нормального распределения, т.е.

. (11)

Так как шум имеет равномерный спектр (см. условие 4) и спектр смеси у(t) также равномерен (вследствие независимости отсчетов), то и полезный сигнал должен иметь равномерный спектр. Вводя спектральную плотность Р = Р 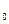/F и вычитая равенство (9) из (11), получаем известную формулу Шэннона — Таллера

C = F log(1 + ). (12)

Таким образом, мы не только определили пропускную способность, но и заодно показали, что она реализуется, если полезный сигнал закодировать так, чтобы его спектр был равномерным в представленной полосе частот, а распределение мгновенных значений — нормальным.

Поиск по сайту: