Простые и сложные проценты

В теории и практике финансово-экономических расчетов принято выделять две схемы начисления процентов:

· Простые проценты – предполагают неизменность величины, с которой происходит начисление, т.е. сумма процента, начисленного в предыдущем периоде, не принимается в расчет в процессе последующего наращения.

· Сложные проценты – предполагают увеличение базы, с которой происходит начисление с каждым шагом времени, т.е. сумма процента, начисленного в предыдущем периоде, присоединяется к основной сумме долга в процессе последующего наращения (капитализируется).

Наращение по простому проценту выглядит следующим образом:

, где

r – процентная ставка;

n – длительность операции (под ней чаще всего подразумевают целое количество лет).

В случае, если длительность операции не равна целому количеству лет, вместо n используют показатель: , где T – количество дней в году.

Дисконтирование по простому проценту можно представить следующим образом:

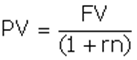
Эта операция называется математическим дисконтированием.

Однако, в практике финансово-экономических расчетов используют еще один вид дисконтирования – банковское дисконтирование, применяющееся, как правило, при учете банком векселей. В этом случае вместо процентной ставки r используют дисконтную (учетную) ставку d. Таким образом, операция дисконтирования выглядит следующим образом:

Наращение с использованием сложной схемы начисления процентов можно представить следующим образом:

Выразив из этой формулы показатель текущей стоимости, можно аналогично осуществить процесс математического дисконтирования:

Таким же образом можно представить процесс банковского дисконтирования: .

В том случае если продолжительность финансовой операции не равна целому количеству лет используют две схемы начисления сложных процентов:

q Сложную –

q Смешанную – , где

w – целое число лет, а f – дробная часть

Графически связь между простой и сложной схемой начисления процентов можно представить следующим образом.

При периоде менее 1 года более выгодна схема начисления простого процента. При периоде более 1 года – схема начисления сложного процента. Если период равен 1 году, то обе схемы дают одинаковый результат.

Поиск по сайту: