Пример проверки адекватности регрессионной модели

1. Шаг Оценим существенность влияния каждой объясняющей переменной (attend, termGPA, priGPAенка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК (), ACT, hwrte согласно приведённому выше примеру, формула (9), на зависимую переменную final, для этого необходимо оценить значимость полученных параметров 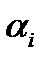(рисунок 2), используя t- критерий Стьюдента.

В оцениваемой модели (формула 9) (рисунок 2) существенные параметры при уровне значимости 1% обозначены ***, 5% - **, 10% - *. Обозначение звёздочками облегчает быстрое оценивание значимости параметров, в рассматриваемом примере существенными являются только константа const и коэффициенты при переменных termGPAенка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК () и ACT (во всех трёх случаях вероятность ошибки при принятии гипотезы об их значимости P-VALUE=0,001%)).

В последнем столбце представляется эмпирический уровень значимости P-VALUE (вероятность допустить ошибку при принятии альтернативной гипотезы, т.е. вероятность того, что значение t-критерия для генеральной совокупности превысит его расчётное значение по данной выборке), который позволяет проверить гипотезы о значимости каждого коэффициента и осуществить отбор существенных (P-value меньше выбранного уровня значимости) и наиболее слабых переменных модели (P-value больше выбранного уровня значимости). В рассмотренном примере самой слабой является переменная PriGPA - вероятность ошибки при принятии гипотезы о её значимости 86,5%, на которую также указывает сообщение в последней строке окна.

Значения столбца Т- Stat (рисунок 2), представляющие собой отношение соответствующих величин в столбцах COEFFICIENT и STDERROR, показывают расчётные значения t- критерий Стьюдента. Согласно методу отбора объясняющих переменных a posteriori предполагается исключение переменных с минимальными (по модулю) значением t- критерия, в рассматриваемом случае - переменных attend, priGPAенка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК (), и hwrte.

2 Шаг. Оценим значимость (пригодность) модели (формула 9) в целом, используя показатели: F-критерий Фишера, коэффициент детерминации (Unadjusted R² и Adjusted R²), сумма квадратов остатков (RSS, Sum of squared residuals), стандартная ошибка регрессии (Standard error of residuals), информационные критерии (Akaike information criterion, Schwarz Bayesian criterion, Hannan-Quinn criterion).

В рассматриваемом примере F-критерий Фишера F-statistic (5, 668) = 66,6869 для p-value < 0,00001. Поскольку p-value меньше выбранного уровня значимости (p=1%) принимается решение о принятии альтернативной гипотезы, т.е. об адекватности модели в целом. Однако = 33,3%, что свидетельствует о невысоком уровне объяснения моделью фактических данных, однако согласно F-тесту, он может быть признан достаточно существенным.

Т.о. в результате анализа рассматриваемой модели на адекватность можно сделать вывод: модель по F-критерию Фишера адекватна, но три коэффициента регрессии (при переменных attend, priGPAенка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК (), и hwrte) незначимы. В этом случае модель пригодна для принятия некоторых решений относительно зависимости переменной final от переменных termgpa и ACT, но не для производства прогнозов.

Пример 2. Согласно вышеизложенным рекомендациям исключим из полученной в Примере 1. модели, формула (9), переменные attend, priGPAенка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК (), и hwrte и повторим рассмотренную последовательность действий для получения линейной регрессионной модели, устанавливающей зависимость переменной FINAL от ACT и termgpa. Получим скорректированную модель final= 10,8+0,339 ACT+ 2,87termgpa+u (рисунок 3), в которой все переменные существенны и модель в целом пригодна для практического использования (согласно рассмотренным выше критериям) для принятия решений и составления прогнозов.

Рисунок 3 - Окно результатов моделирования с применением 1МНК, скорректированная модель

Сохраним значения остатков данной модели как отдельную переменную RESIDUALS набора attend.gdt при помощи функции Save\Residuals окна результатов моделирования (рисунок 3). После нажатия кнопки ОК диалогового окна, данная переменная добавится в список переменных рассматриваемого набора данных attend.gdt. Аналогичным образом сохраним модельные значения результативного признака (final) как FITSfinal при помощи функции Save\Fitted Values.

Поиск по сайту: