Пример обнаружения гетероскедастичности в Gretl

Шаг 1. Выберем команду меню File\Open Data\Sample File …и на закладке Verbeek двойным щелчком мыши откроем встроенный разработчиками набор данных bwages.gdt ( рисунок 3).

Рисунок 3 – Открытие встроенного набора данных bwages.gdt

Шаг 2. Просмотрим текстовую информацию о наборе данных, выбрав команду Data\Print Description. В открывшемся окне (рисунок 4) появится информация о наборе данных bwages.gdt в целом и о каждой переменной.

Файл содержит 1472 наблюдения, относящихся к 1994, группе бельгийских семей Европейского Сообщества. Тип данных undated (срез данных для фиксированного момента времени – cross-sectional). Переменные:

wage – заработная плата в час, до выплаты налогов (Евро),

educ – уровень образования от 1 (низкий) до 5 (высокий),

exper – опыт работы (лет)

male – фиктивная переменная, принимает значение «1», если мужчина и «0», если женщина. Также представлены логарифмы переменных wage, educ, exper.

Требуется оценить влияние уровня образования (educ) в бельгийских семьях на величину заработной платы (wage), используя фактические данные 1994 года по 1472 семьям.

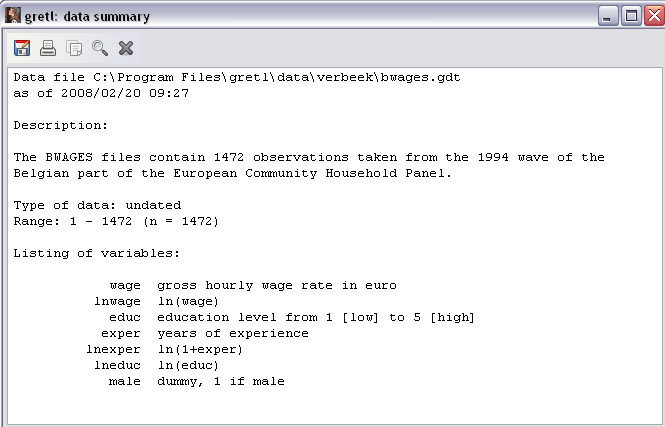
Рисунок 4 – Текстовое описание набора данных bwages.gdt

Шаг 3. Проведём предварительный графический анализ данных, построив диаграммы рассеяния пар переменных educ -wage, exper-wage, male –wage.

Выберем команду меню View\Multiple graphs Vars\ X-Y scatters… (рисунок 5). В открывшемся окне выберем переменную wage (по оси ОУ), а переменные educ, exper, male (по оси ОХ) нажатием кнопок «Choose» и «Add» соответственно.

Как показывает рисунок 6, дисперсия wage (которую будем рассматривать как зависимую переменную Y) увеличивается при росте каждого из факторов educ, exper, male(которые будем рассматривать как независимые переменные, Хi), что свидетельствует о гетероскедастичности.

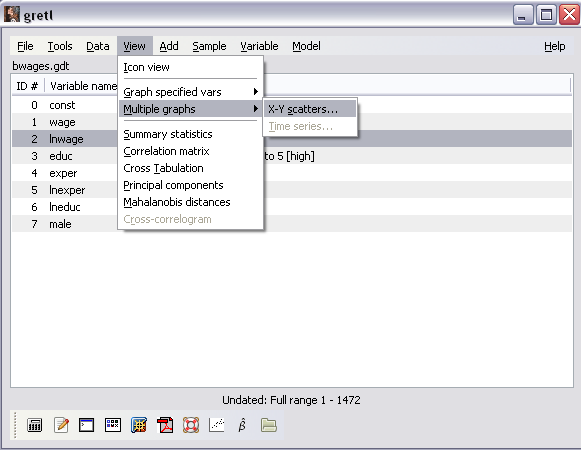
Рисунок 5 – Построение диаграмм рассеяния educ-wage, exper-wage, male-wage

Рисунок 6 – Диаграммы рассеяния пар переменных educ -wage, exper-wage, male –wage

Шаг 4. Проведём оценивание модели 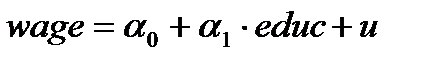обычным методом наименьших квадратов 1МНК (OLS).Для этого выберем команду меню Model\Ordinary Least Squares… и в открывшемся окне спецификации модели выберем зависимую переменную wage при помощи кнопки «Choose» и независимую переменную educ при помощи кнопки «Add». После нажатия кнопки ОК появится окно с результатами моделирования (рисунок 7).

Рисунок 7 – Построение модели 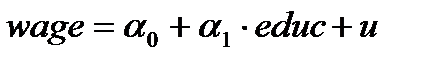методом 1МНК (OLS)

По результатам 1МНК в полученной модели параметры 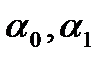являются значимыми при уровнях значимости 5% и 1%, поскольку P-VALUE=0,001%<1%< 5% (принимаем альтернативную гипотезу Н1: ).

Хотя по данным 1МНК можно установить существенность влияния переменной educ (образование) на переменную wage (з.пл.), необходимо сделать поправку на гетероскедастичность в связи с ошибочностью расчёта величин COEFFICIENT, STDERROR и T-STAT и ненадёжностью результатов данного оценивания -возможностью принятия неправильной гипотезы.

Сохраним величины квадратов остатковв отдельную переменную usq1набора данных, обратившись к команде Save\Squared Residuals меню окна результатов моделирования (рисунок 7) и нажав кнопку ОК.

Шаг 5. Подтвердим наличие гетероскедастичности, используя формальный тест Уайта. Обратимся к команде Tests\Heteroskedasticity меню окна результатов моделирования (рисунок 8).

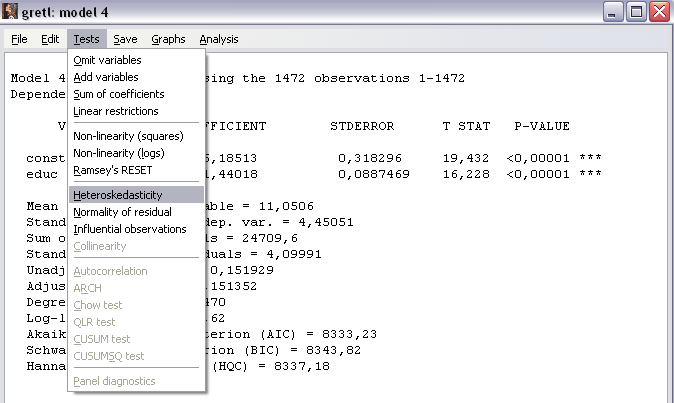Рисунок 8 – Проведение теста Уайта на гетероскедастичность

В результате теста получим вспомогательную модель регрессии остатков относительно переменной educ и её квадрата 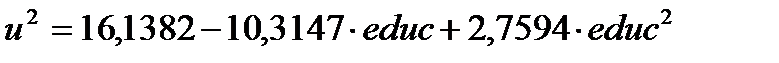(рисунок 9).

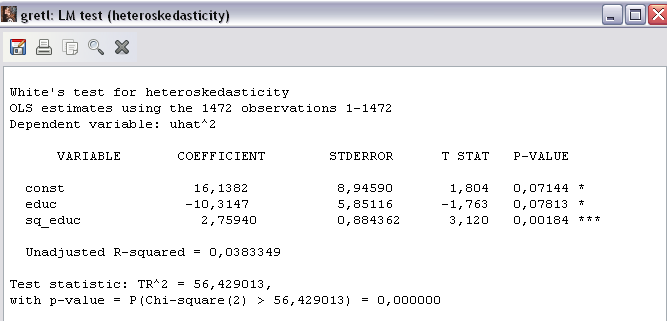
Рисунок 9 – Окно результатов теста Уайта на гетероскедастичность

Проверим общую значимость (адекватность в целом) данной модели, используя критерий .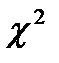

В окне результатов теста (рисунок 9) значение p-value для статистики теста n*R² (TR^2) составило 0,000%, что меньше уровней значимости 1% и 5% и свидетельствует о наличии гетероскедастичности (адекватности вспомогательной модели, неравенстве нулю всех её параметров).

Т.о. отвергаем гипотезу Ho о гомоскедастичности (равенстве нулю всех её параметров), поскольку расчётное значение статистики n*R² =TR^2=56,429 больше 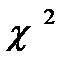критического ().

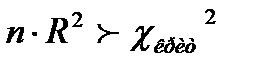Найдём 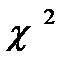критическое для уровня значимости 1%, обратившись к команде основного меню Tools\Statistical Tables и введя в открывшемся окне на закладке Chi-Square число степеней свободы (2, равное числу регрессоров 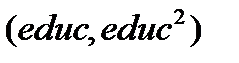вспомогательной модели) и уровень значимости 0.001 (рисунок 10). Получим 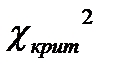=13,8155 (Critical value).

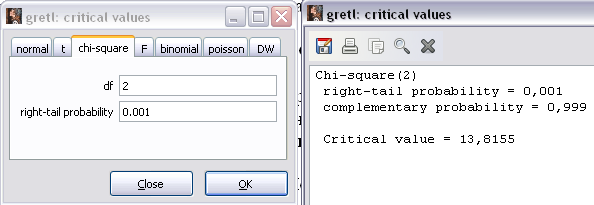
Рисунок 10 – Нахождение критического значения 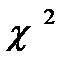для df=2, p=1%

Построим график данного 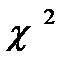распределения, выбрав команду основного меню Tools\Distribution Graphs, закладку Chi-square и df=2 в открывшемся окне (рисунок 11).

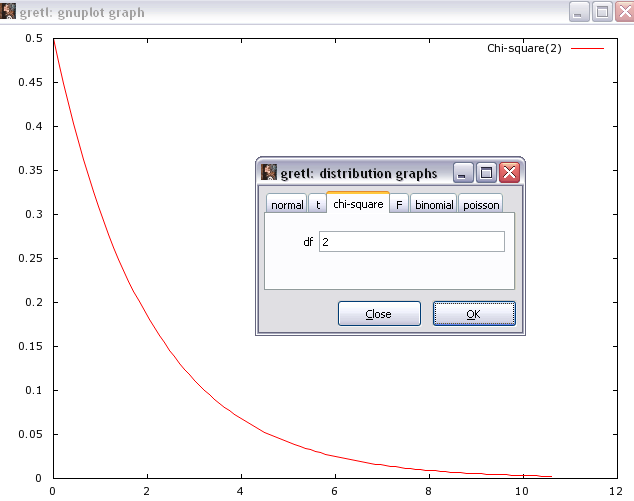
Рисунок 11 - График 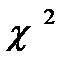распределения, df=2

Поиск по сайту: