ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ О ЛИНЕЙНОМ РЕГРЕССИОННОМ АНАЛИЗЕ

Целью регрессионного анализа является оценка функциональной зависимости результативного признака (y) от факторных . Формулы (1) и (2) представляют собой линейные модели парной и множественной регрессии соответственно.

, (1)

, (2)

где y — фактическое значение результативного признака;

- признак-фактор;

a_i – параметр регрессионной модели;

— случайная ошибка (остаток), характеризующая отклонения реального значения результативного признака от теоретического. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

Оценивание параметров линейной модели основан на обычном или одношаговом методе наименьших квадратов (1МНК или OLS – Ordinary Least Squares).

Этот метод позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (y) от расчетных (теоретических) минимальна, формула (3).

, (3)

Статистическое моделирование связи методом линейного регрессионного анализа осуществляется в 3 этапа:

A) Оценка параметров линейной регрессионной модели методом 1МНК

Вектор оценок параметров модели (2) определяется выражением 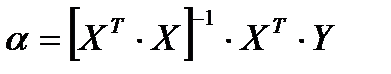(4). (4)

B) Проверка адекватности регрессионной модели (проверки значимости индивидуальных оценок коэффициентов модели с помощью t- критерия Стьюдента и оценка значимости уравнения регрессии в целом с помощью F-критерия Фишера)

На первом шаге проверки адекватности (качества) модели оценивается существенность влияния каждой объясняющей переменной енка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК (), на зависимую переменную y, для этого необходимо оценить значимость полученных параметров 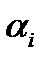, используя t- критерий Стьюдента, формула (5). Значимость параметра определяется путём проверки нулевой гипотезы о равенстве его нулю (для выбранного уровня значимости).

,(5)

где - оценка -го коэффициента модели, COEFFICIENT;

-оценка дисперсии параметра , = STDERROR.

На втором шаге проверки адекватности модели оценивается её значимость (пригодность) в целом, используя показатели: F-критерий Фишера, формула (6), коэффициент детерминации , формула (7), (Unadjusted R² и Adjusted R²), сумма квадратов остатков RSS Sum of squared residuals), стандартная ошибка регрессии (Standard error of residuals), информационные критерии (Akaike information criterion, Schwarz Bayesian criterion, Hannan-Quinn criterion).

Значимость регрессии проверяется путём проверки нулевой гипотезы о равенстве нулю всех параметров модели (для выбранного уровня значимости).

, (6)

где - коэффициент детерминации - часть вариации (дисперсии) зависимой переменной y, которая объясняется уравнением регрессии, UNADJUSTED R².

, (7)

- число наблюдений;

k – число коэффициентов факторов.

При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:

- Построенная модель на основе ее проверки по F-критерию Фишера в целом

адекватна, и все коэффициенты регрессии значимы. Такая модель может быть

использована для принятия решений к осуществлению прогнозов.

- Модель по F-критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для производства прогнозов.

- Модель по F-критерию Фишера адекватна, но все коэффициенты регрессии незначимы. Поэтому модель полностью считается неадекватной. На ее основе не принимаются решения и не осуществляются прогнозы.

Поиск по сайту: